
Министерство образования и науки Российской федерации.
Государственное образовательное учреждение высшего
профессионального образования.
«Ивановский государственный энергетический университет
имени В.И.Ленина»
Кафедра ПОКС.
Курсовая работа по вычислительной математике
Вариант №18
Выполнил: студент группы 3-42
Ромашов Д.Е.
Проверил: к.ф.м.н. проф. Гусев В.А.
Иваново 2011
Задание.
Построить решение дифференциального уравнения.
Подобрать многочлен, наилучшим образом описывающий полученное решение и определить корни уравнения на полученном интервале.


Решение.
Поиск решения дифференциального уравнения будет производиться с использованием метода Рунге-Кутта 4-го порядка, так как данный метод обеспечивает большую точность по сравнению с методами низших порядков.
Метод Рунге-Кутта численного решения системы обыкновенных дифференциальных уравнений.
Представим ДУ 2 порядка в виде системы ДУ 1 порядка:
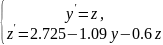

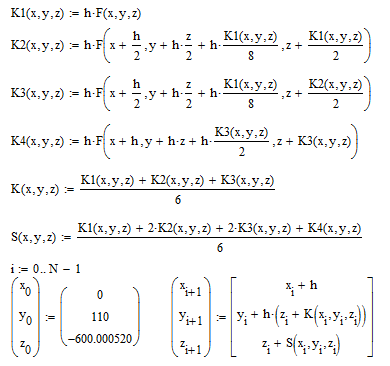



Выбор шага.
Для выбора установим необходимую точность значений 0,0001.
Далее, при различных шагах сравним
значения
 при соответствующих
при соответствующих
 .
.
h=0.5 h=0.25 h=0.125



h=0.625 h=0.0625 h=0.03125


Разница между значениями, при шагах h=0.0625 h=0.03125, не существенная, поэтому остановимся на шаге h=0.03125.
По полученным значениям построим график (см. рис.1).
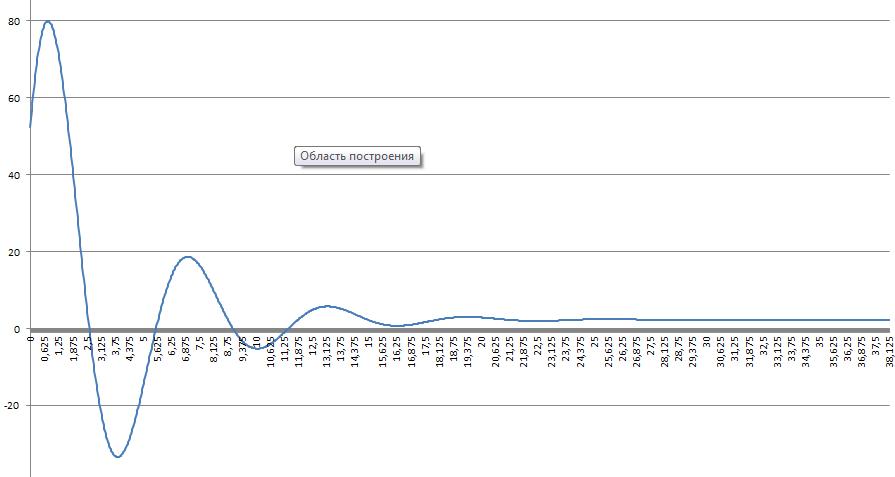
Рис. 1. График функции y(x), построенный по точкам.
Для интерполяции возьмем точность ε = 0.01. Будем подбирать полином на отрезке [0;25], так как дальше значение функции не изменяется.
На всем промежутке [0;25] подобрать полином с указанной точностью не получится, поэтому разобьем его на 3 отрезка [0;3], [3;11], [11;30], и на каждом подберем полином методом наименьших квадратов.
Подберем полином на отрезке [0;0.4].
Составим систему уравнений:
A×C=B. (1)
Элементы матриц A и B считаем так:
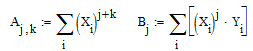
где i = 0,1…M, M=(a-b)/h, j = 0…N, k = 0…N, здесь N – степень полинома.
Решив систему (1), найдем коэффициенты полинома Ci.
Наиболее подходит полином 14 степени. Коэффициенты полиномов:

Рис. 2. График функции y(x), построенный по точкам.
Для интерполяции возьмем точность ε = 0.01. Будем подбирать полином на отрезке [0;1.2], так как дальше значение функции не изменяется.
На всем промежутке [0;1.2] подобрать полином с указанной точностью не получится, поэтому разобьем его на 3 отрезка [0;0.4], [0.4;0.8], [0.8;1.2], и на каждом подберем полином методом наименьших квадратов.
Подберем полином на отрезке [0;0.4].
Составим систему уравнений: A×C=B.(1)
Элементы матриц A и B считаем так:
где i = 0,1…M, M=(a-b)/h, j = 0…N, k = 0…N, здесь N – степень полинома.
Решив систему (1), найдем коэффициенты полинома Ci.
Наиболее подходит полином 14 степени. Коэффициенты полиномов:
|
P13 |
P14 |
P15 |
C0 |
1.09533E+002 |
1.09974E+002 |
1.10033E+002 |
C1 |
-4.02032E+002 |
-5.88794E+002 |
-6.14349E+002 |
C2 |
-6.28007E+004 |
-4.43537E+004 |
-4.17640E+004 |
C3 |
1.10337E+006 |
3.19157E+005 |
2.05988E+005 |
C4 |
-1.68383E+007 |
1.22381E+006 |
3.90648E+006 |
C5 |
2.55894E+008 |
2.83066E+006 |
-3.58866E+007 |
C6 |
-2.56932E+009 |
-2.69609E+008 |
9.32119E+007 |
C7 |
1.61400E+010 |
2.11669E+009 |
-1.71393E+008 |
C8 |
-6.59969E+010 |
-7.96545E+009 |
1.91667E+009 |
C9 |
1.80288E+011 |
1.93097E+010 |
-1.01342E+010 |
C10 |
-3.28131E+011 |
-4.32157E+010 |
1.81625E+010 |
C11 |
3.82423E+011 |
1.04800E+011 |
8.74901E+009 |
C12 |
-2.57458E+011 |
-1.97890E+011 |
-6.21542E+010 |
C13 |
7.55679E+010 |
2.14236E+011 |
2.52451E+010 |
C14 |
- |
-9.71004E+010 |
9.76004E+010 |
C15 |
- |
- |
-9.25891E+010 |
|
2.31877E+000 |
7.68241E-003 |
2.82897E-002 |

xi |
yi |
Pn(xi) |
|yi-Pn(xi)| |
0.00000 |
110.00000 |
110.00082 |
0.00082 |
0.01000 |
99.97210 |
99.96896 |
0.00314 |
0.02000 |
83.20474 |
83.20671 |
0.00196 |
0.03000 |
61.92708 |
61.93008 |
0.00300 |
0.04000 |
38.51095 |
38.51113 |
0.00018 |
0.05000 |
15.24716 |
15.24440 |
0.00276 |
0.06000 |
-5.84578 |
-5.84905 |
0.00327 |
0.07000 |
-23.16752 |
-23.16877 |
0.00125 |
0.08000 |
-35.62865 |
-35.62693 |
0.00172 |
0.09000 |
-42.68823 |
-42.68452 |
0.00371 |
Отклонение меньше ε, это допустимо.

Рис. 3. График полинома на промежутке [0;0.4].
