25. Признак параллельности прямой и плоскости

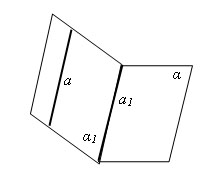
Теорема Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Доказательство Пусть α - плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана.

26.

Параллельность плоскостей Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β.

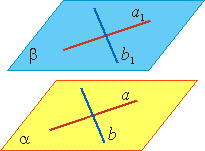
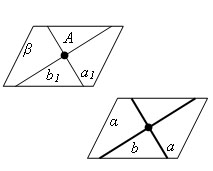
Признак параллельности двух плоскостей Теорема. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны. Если а∥а1 и b∥b1, то α∥β.

27. Существование плоскости, параллельной данной плоскости

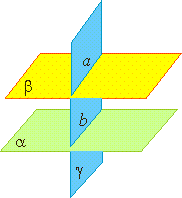
Теорема Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну. Доказательство Проведем в данной плоскости α какие-нибудь две пересекающиеся прямые a и b. Через данную точку A проведем параллельные им прямые a1 и b1. Плоскость β, проходящая через прямые a1 и b1, по теореме о признаке параллельности плоскостей параллельна плоскости α. 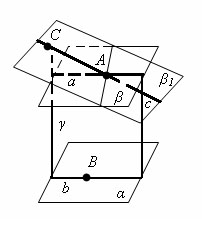Предположим, что через точку A проходит другая плоскость β1, тоже параллельная плоскости α. Отметим на плоскости β1 какую-нибудь точку С, не лежащую в плоскости β. Проведем плоскость γ через точки A, С и какую-нибудь точку B плоскости α. Эта плоскость пересечет плоскости α, β и β1 по прямым b, a и с. Прямые a и с не пересекают прямую b, так как не пересекают плоскость α. Следовательно, они параллельны прямой b. Но в плоскости γ через точку A может проходить только одна прямая, параллельная прямой b. что противоречит предположению. Теорема доказана.

28. Свойства параллельных плоскостей

Вели α∥β и они пересекаются с γ, то а∥b. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Если α∥β и AB∥CD, то АВ = CD. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

29.

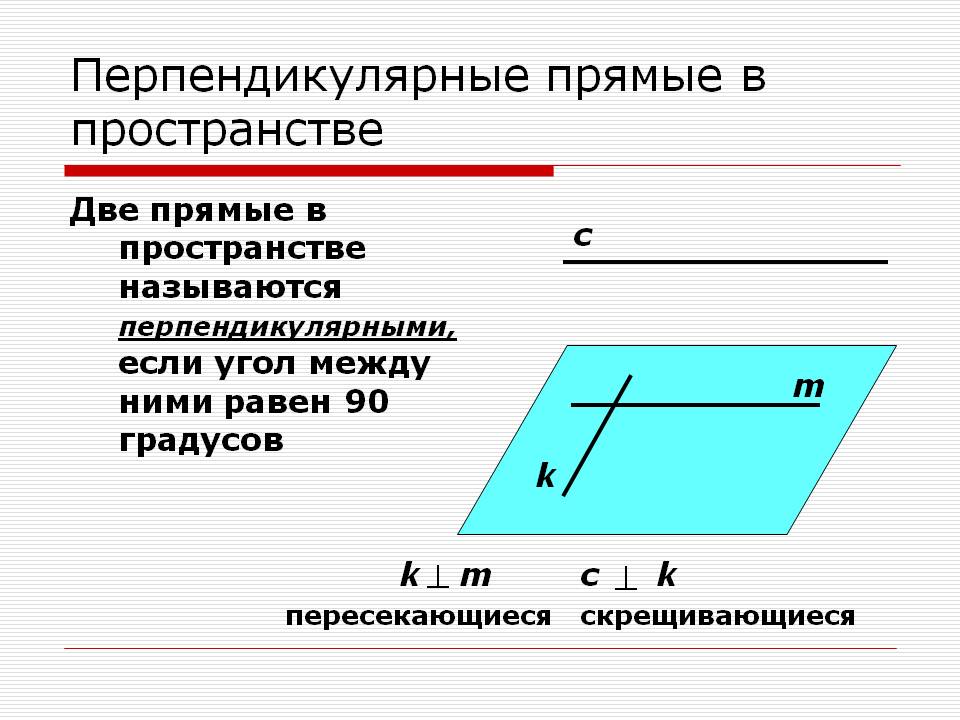
Перпендикулярные прямые в пространстве. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90 градусов. c. m. k. k. m. c. k. Пересекающиеся. Скрещивающиеся.

30.

Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Доказательство: Пусть а прямая, перпендикулярная прямым b и c в плоскости . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости . Проведем произвольную прямую х через точку А в плоскости и покажем, что она перпендикулярна прямой а. Проведем в плоскости произвольную прямую, не проходящую через точку А и пересекающую прямые b, c и х. Пусть точками пересечения будут В, С и Х. Отложим на прямой а от точки А в разные стороны равные отрезки АА1 и АА2. Треугольник А1СА2 равнобедренный, так как отрезок АС является высотой по условию теоремы и медианой по построению (АА1=АА2). по той же причине треугольник А1ВА2 тоже равнобедренный. Следовательно, треугольники А1ВС и А2ВС равны по трем сторонам. Из равенства треугольников А1ВС и А2ВС следует равенство углов А1ВХ и А2ВХ и, следовательно равенство треугольников А1ВХ и А2ВХ по двум сторонам и углу между ними. Из равенства сторон А1Х и А2Х этих треугольников заключаем, что треугольник А1ХА2 равнобедренный. Поэтому его медиана ХА является также высотой. А это и значит, что прямая х перпендикулярна а. По определению прямая а перпендикулярна плоскости . Теорема доказана.

31.32

Теорема 2 1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
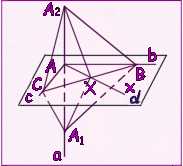
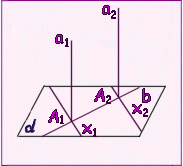
Доказательство: Пусть а1 и а2 - 2 параллельные прямые и плоскость, перпендикулярная прямой а1. Докажем, что эта плоскость перпендикулярна и прямой а2. Проведем через точку А2 пересечения прямой а2 с плоскостью произвольную прямую х2 в плоскости . Проведем в плоскости через точку А1 пересечения прямой а1 с прямую х1, параллельную прямой х2. Так как прямая а1 перпендикулярна плоскости , то прямые а1 и x1перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а2 и х2 тоже перпендикулярны. Таким образом, прямая а2 перпендикулярна любой прямой х2 в плоскости . А это ( по определению )значит, что прямая а2 перпендикулярна плоскости . Теорема доказана. Смотри также опорную задачу №2.
Теорема 3 2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
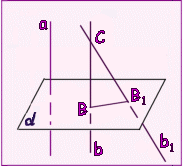
Доказательство: Пусть а и b - 2 прямые, перпендикулярные плоскости . Допутим, что прямые а и b не параллельны. Выберем на прямой b точку С, не лежащую в плоскости . Проведем через точку С прямую b1, параллельную прямой а. Прямая b1 перпендикулярна плоскости по теореме 2. Пусть В и В1 - точки пересечения прямых b и b1 с плоскостью . Тогда прямая ВВ1 перпендикулярна пересекающимся прямым b и b1. А это невозможно. Мы пришли к противоречию. Теорема доказана.

33. Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной. 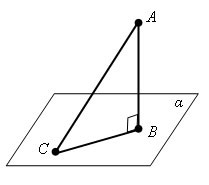AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция.

Формулировка теоремы

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна к наклонной.

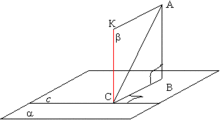
  Доказательство

Пусть AB — перпендикуляр к плоскости α, AC — наклонная и c — прямая в плоскости α, проходящая через точку C и перпендикулярная проекции BC. Проведем прямую CK параллельно прямой AB. Прямая CK перпендикулярна плоскости α (так как она параллельна AB), а значит, и любой прямой этой плоскости, следовательно, CK перпендикулярна прямой c. Проведем через параллельные прямые AB и CK плоскость β (параллельные прямые определяют плоскость, причем только одну). Прямая c перпендикулярна двум пересекающимся прямым, лежащим в плоскости β, это BC по условию и CK по построению, значит, она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит, перпендикулярна и прямой AC.

Теорема о трех перпендикулярах

Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а₁ — проекция наклонной а на плоскость α.

Сформулируем теорему о трех перпендикулярах:

Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

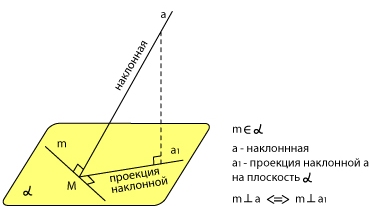
На рисунке показаны все три перпендикуляра.

Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.

34.

Теорема 5 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство: Пусть - плоскость , b - перпендикулярная ей прямая, - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и b плоскость . Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскости и перпендикулярны. Теорема доказана.

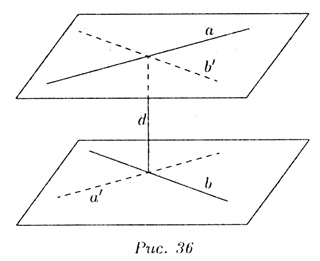
35. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, и он перпендикулярен каждой из этих прямых.

Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, каждая из которых проходит через одну прямую параллельно другой.

На рис. 36 имеем две скрещивающиеся прямые a и b. Через каждую из них проведена плоскость (плоскость проходит через а, плоскость проходит через b), параллельная другой прямой.

Отрезки параллельных прямых, заключенные между параллельных прямых, равны.