
28.2 Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zl т. е. z=z1-z2, если z+z2=z1.
Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:
z=z1-z2=(x1-x2)+i(y1-y2). (28.2)
Из равенства (28.2) следует, что геометрически комплексные числа вычитаются как векторы (см. рис. 165).
Непосредственно из рисунка видно, что |z1-z2|≥|z1|-|z2|. Отметим, что
![]()
т. е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.
Поэтому, например, равенство |z-2i|=1 определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки z0=2i, т. е. окружность с центром в z0=2i и радиусом 1.
19.
Аксиома
1.
Через
любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом
только одна![]()
Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). |
|
Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. |
|

20.
Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна. |
|
21.
Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
|
|
22. Уравнение плоскости, проходящей через три точки
Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.
Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы были компланарны.
() = 0
23.
Определение 2.1.
Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не имеют общих точек.
Если две прямые a и b параллельны, то, как и в планиметрии, пишут a || b . В пространстве прямые могут быть размещены так, что они не пересекаются и не параллельны. Этот случай является особым для стереометрии.
Определение 2.2.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися .
Теорема 2.1.
Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.
24.
Признак параллельности прямых |
|
|
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Через точку вне данной прямой можно пронести прямую, параллельную этой пряиой, и притом только одну. Это утверждение сводится к аксиоме о параллельных в плоскости. Теорема. Две прямые, параллельные третьей прямой, параллельны. Пусть прямые b и с параллельны прямой а. Падо доказать, что b || с.
Случай,
когда прямые а, b и с лежат и одной
плоскости, рассмотрен в планиметрии,
его опускаем. Предположим, что а, b и с
не лежит в одной плоскости. Но так как
две параллельные прямые расположены
в одной плоскости, то можно считать,
что а и b расположены и плоскости
|



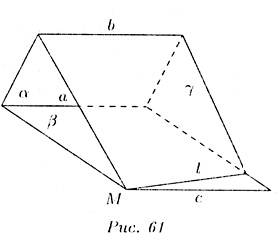
 (рис.
61). На прямой с отметим точку (любую) М
и через прямую b и точку M проведем
плоскость
(рис.
61). На прямой с отметим точку (любую) М
и через прямую b и точку M проведем
плоскость