- •Министерство науки и образования Российской Федерации
- •1. Кинематика
- •1.1 Выбор λ и длины шатуна
- •1.2 Перемещение поршня
- •1.3 Скорость поршня
- •1.4 Ускорение поршня
- •Динамика двс
- •2.1 Силы давления газов
- •2.2 Приведение масс частей кривошипно-шатунного механизма
- •2.3 Силы инерции
- •2.4 Суммарные силы, действующие в кривошипно-шатунном механизме
- •2.5 Суммарный крутящий момент, действующий в двигателе
- •2.6 Уравновешивание двигателя
- •Заключение
- •Список использованной литературы
2.2 Приведение масс частей кривошипно-шатунного механизма
По характеру движения массы деталей кривошипно-шатунного механизма можно разделить на движущиеся возвратно-поступательно (поршневая группа и верхняя головка шатуна); совершающие вращательное движение (коленчатый вал и нижняя головка шатуна) и совершающие сложное плоскопараллельное движение (стержень шатуна).
Для упрощения динамического расчета действительный кривошипно-шатунный механизм заменяется эквивалентной системой сосредоточенных масс.
Массу поршневой
группы
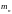 считают сосредоточенной на оси поршневого
пальца в точке А (рис. 9а). Массу шатунной
группы
считают сосредоточенной на оси поршневого
пальца в точке А (рис. 9а). Массу шатунной
группы
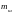 заменяют двумя массами, одна из которых
(
заменяют двумя массами, одна из которых
(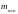 )
сосредоточена на оси поршневого пальца
в точке А, а другая (
)
– на оси кривошипа в точке В.
)
сосредоточена на оси поршневого пальца
в точке А, а другая (
)
– на оси кривошипа в точке В.
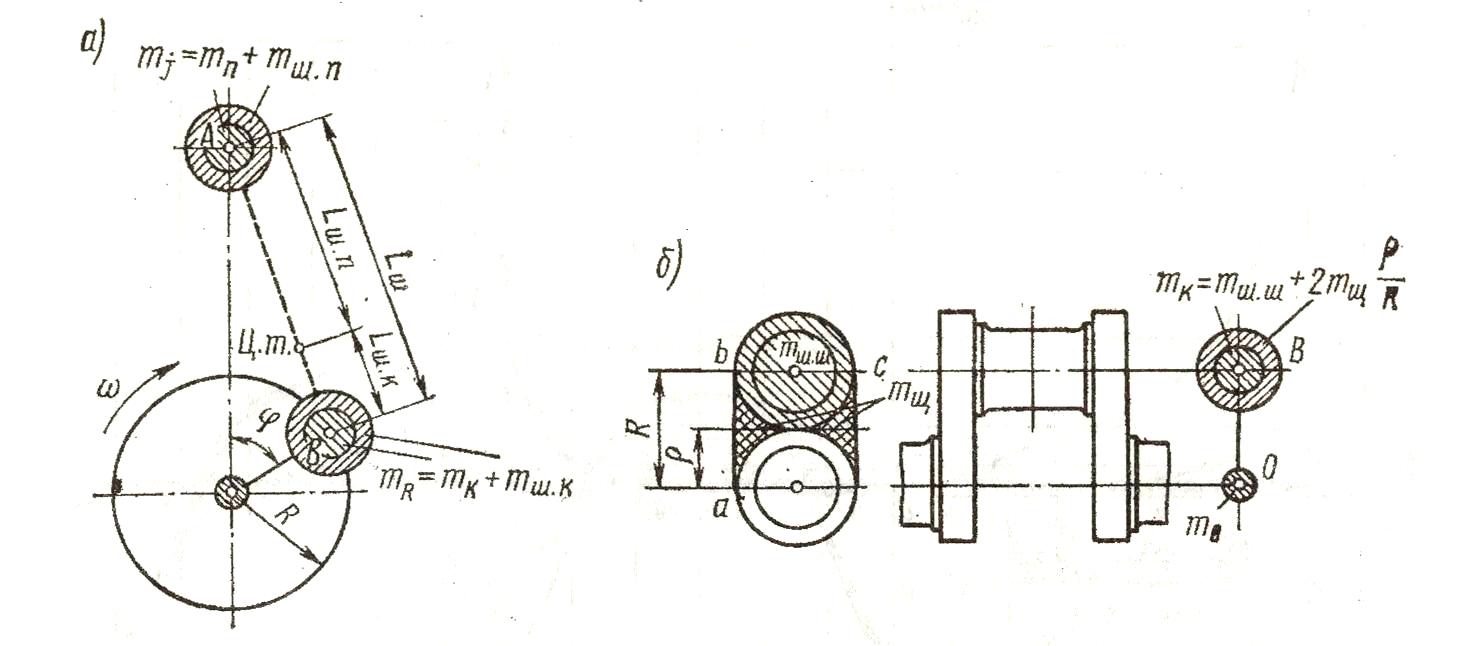
Рис. 6 – Система сосредоточенных масс, динамически эквивалентная КШМ:
а – приведенная система КШМ, б – приведение масс кривошипа
Для
большинства автомобильных и тракторных
двигателей при расчетах можно принимать
 ,
а
,
а
 .
.
Массу
кривошипа заменяют двумя массами,
сосредоточенными на оси кривошипа в
точке В ( )
и на оси коренной шейки в точке О (
)
и на оси коренной шейки в точке О (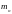 )
(рис. 9б).
)
(рис. 9б).
Таким
образом, система сосредоточенных масс,
динамически эквивалентная
кривошипно-шатунному механизму, состоит
из массы
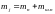 ,
сосредоточенной в точке А и имеющей
возвратно-поступательное движение, и
массы
,
сосредоточенной в точке А и имеющей
возвратно-поступательное движение, и
массы
 (для рядного двигателя, согласно [2]).
(для рядного двигателя, согласно [2]).
При выполнении динамического расчета двигателя значения , , подсчитываются с чертежа, либо выбираются из стандартных значений.
Выберем , , из рекомендованных значений [2], затем уточним методом экстраполяции.
Тогда

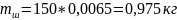

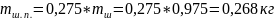
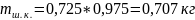
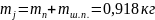 .
.
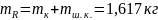 .
.
2.3 Силы инерции
Силы инерции,
действующие в кривошипно-шатунном
механизме, в соответствии с характером
движения приведенных масс подразделяют
на силы инерции поступательно движущихся
масс
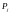 и центробежные силы инерции вращающихся
масс
и центробежные силы инерции вращающихся
масс
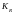 .
.
Сила инерции от возвратно-поступательно движущихся масс находится по формуле:
 .
.
В данном уравнении знак минус показывает, что сила инерции направлена в сторону, противоположную ускорению. Силы инерции возвратно-поступательно движущихся масс действуют по оси цилиндра и как силы давления газов, являются положительными, если они направлены к оси коленчатого вала, и отрицательными, если они направлены от коленчатого вала.
Кривую силы инерции возвратно-поступательно движущихся масс строят аналогично кривой ускорения поршня (рис. 10).
Произведем
расчет сил инерции через каждые
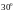 поворота кривошипа, полученные данные
сведем в таблицу №6.
поворота кривошипа, полученные данные
сведем в таблицу №6.
Таблица №6 – Значения сил инерции возвратно-поступательно движущихся масс
|
|
|
|
0 |
-2,3075 |
370 |
-2,2503 |
30 |
-1,8188 |
390 |
-1,8188 |
60 |
-0,6632 |
420 |
-0,6632 |
90 |
0,4906 |
450 |
0,4906 |
120 |
1,1537 |
480 |
1,1537 |
150 |
1,3282 |
510 |
1,3282 |
180 |
1,3264 |
540 |
1,3264 |
210 |
1,3282 |
570 |
1,3282 |
240 |
1,1537 |
600 |
1,1537 |
270 |
0,4906 |
630 |
0,4906 |
300 |
-0,6632 |
660 |
-0,6632 |
330 |
-1,8188 |
690 |
-1,8188 |
360 |
-2,3075 |
720 |
-2,3075 |

Рис. 7 – Зависимость сил инерции возвратно-поступательно движущихся масс от угла поворота КВ
Центробежная сила инерции вращающихся масс:
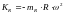 .
Это постоянная величина (при
.
Это постоянная величина (при
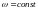 ),
действует по радиусу кривошипа и
направлена от оси коленчатого вала.
),
действует по радиусу кривошипа и
направлена от оси коленчатого вала.
Центробежная
сила инерции
является результирующей двух сил (для
рядного двигателя):
 ,
где
,
где
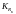 и
и
 -
силы инерции вращающихся масс кривошипа
шатуна соответственно. Таким образом:
-
силы инерции вращающихся масс кривошипа
шатуна соответственно. Таким образом:
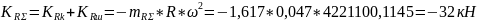 .
.