Заключение

Итак, в ходе выполнения данной курсовой работы, были изучены характеристики электромагнитного поля элементарного электрического излучателя, построены диаграммы направленности. Были получены формулы для относительных амплитуд, показывающих, насколько сильно меняются составляющие вектора напряженности электрического и магнитного полей в зависимости от расстояния до излучателя, и посчитаны их численные значения для данного интервала.

Список используемой литературы

1) Коваленко А.Н., Щербицкий А.Н. «Электродинамика и распространение волн» Ч. 1, «Основы теории электромагнитного поля», МИРЭА 1999

2) Коваленко А.Н., Щербицкий А.Н. «Электродинамика и распространение волн» Ч. 2, «Граничные задачи электродинамики» МИРЭА 2001

3) Коваленко А.Н., Щербицкий А.Н. «Электродинамика и распространение волн» Ч. 3, «Распространение радиоволн» МИРЭА 2004

4) Исаков В.Н., Коваленко А.Н. «Электродинамика и распространение радиоволн: методические указания по выполнению лабораторных работ» МИРЭА 2011

5) Никольский В.В, Никольская Т.И., «Электродинамика и распространение радиоволн» М:Наука, 1989

6) Никольский В.В., «Математический аппарат электродинамики», М:МИРЭА, 1973

7) Гончаренко В.М., Гурин Н.Н., «Устройство сверхвысоких частот и антенны», М:МИРЭА, 2010

Приложение

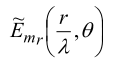
1.0000 0.9397 0.7660 0.5000 0.1736 0.1736 0.5000 0.7660 0.9397 1.0000

0.2412 0.2267 0.1848 0.1206 0.0419 0.0419 0.1206 0.1848 0.2267 0.2412

0.1065 0.1001 0.0816 0.0532 0.0185 0.0185 0.0532 0.0816 0.1001 0.1065

0.0597 0.0561 0.0458 0.0299 0.0104 0.0104 0.0299 0.0458 0.0561 0.0597

0.0382 0.0359 0.0293 0.0191 0.0066 0.0066 0.0191 0.0293 0.0359 0.0382

0.0265 0.0249 0.0203 0.0133 0.0046 0.0046 0.0133 0.0203 0.0249 0.0265

0.0195 0.0183 0.0149 0.0097 0.0034 0.0034 0.0097 0.0149 0.0183 0.0195

0.0149 0.0140 0.0114 0.0075 0.0026 0.0026 0.0075 0.0114 0.0140 0.0149

0.0118 0.0111 0.0090 0.0059 0.0020 0.0020 0.0059 0.0090 0.0111 0.0118

0.0095 0.0090 0.0073 0.0048 0.0017 0.0017 0.0048 0.0073 0.0090 0.0095

0.0079 0.0074 0.0060 0.0039 0.0014 0.0014 0.0039 0.0060 0.0074 0.0079

0.0066 0.0062 0.0051 0.0033 0.0011 0.0011 0.0033 0.0051 0.0062 0.0066

0.0056 0.0053 0.0043 0.0028 0.0010 0.0010 0.0028 0.0043 0.0053 0.0056

0.0049 0.0046 0.0037 0.0024 0.0008 0.0008 0.0024 0.0037 0.0046 0.0049

0.0042 0.0040 0.0032 0.0021 0.0007 0.0007 0.0021 0.0032 0.0040 0.0042

0.0037 0.0035 0.0029 0.0019 0.0006 0.0006 0.0019 0.0029 0.0035 0.0037

0.0033 0.0031 0.0025 0.0016 0.0006 0.0006 0.0016 0.0025 0.0031 0.0033

0.0029 0.0028 0.0023 0.0015 0.0005 0.0005 0.0015 0.0023 0.0028 0.0029

0.0026 0.0025 0.0020 0.0013 0.0005 0.0005 0.0013 0.0020 0.0025 0.0026

0.0024 0.0022 0.0018 0.0012 0.0004 0.0004 0.0012 0.0018 0.0022 0.0024

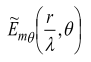
0 0.3420 0.6428 0.8660 0.9848 0.9848 0.8660 0.6428 0.3420 0.0000

0 0.1771 0.3329 0.4485 0.5101 0.5101 0.4485 0.3329 0.1771 0.0000

0 0.1189 0.2235 0.3011 0.3424 0.3424 0.3011 0.2235 0.1189 0.0000

0 0.0894 0.1680 0.2264 0.2574 0.2574 0.2264 0.1680 0.0894 0.0000

0 0.0716 0.1346 0.1813 0.2062 0.2062 0.1813 0.1346 0.0716 0.0000

0 0.0597 0.1122 0.1512 0.1719 0.1719 0.1512 0.1122 0.0597 0.0000

0 0.0512 0.0962 0.1296 0.1474 0.1474 0.1296 0.0962 0.0512 0.0000

0 0.0448 0.0842 0.1135 0.1290 0.1290 0.1135 0.0842 0.0448 0.0000

0 0.0398 0.0749 0.1009 0.1147 0.1147 0.1009 0.0749 0.0398 0.0000

0 0.0359 0.0674 0.0908 0.1032 0.1032 0.0908 0.0674 0.0359 0.0000

0 0.0326 0.0613 0.0825 0.0939 0.0939 0.0825 0.0613 0.0326 0.0000

0 0.0299 0.0562 0.0757 0.0860 0.0860 0.0757 0.0562 0.0299 0.0000

0 0.0276 0.0518 0.0699 0.0794 0.0794 0.0699 0.0518 0.0276 0.0000

0 0.0256 0.0481 0.0649 0.0738 0.0738 0.0649 0.0481 0.0256 0.0000

0 0.0239 0.0449 0.0605 0.0688 0.0688 0.0605 0.0449 0.0239 0.0000

0 0.0224 0.0421 0.0568 0.0645 0.0645 0.0568 0.0421 0.0224 0.0000

0 0.0211 0.0397 0.0534 0.0608 0.0608 0.0534 0.0397 0.0211 0.0000

0 0.0199 0.0375 0.0505 0.0574 0.0574 0.0505 0.0375 0.0199 0.0000

0 0.0189 0.0355 0.0478 0.0544 0.0544 0.0478 0.0355 0.0189 0.0000

0 0.0179 0.0337 0.0454 0.0516 0.0516 0.0454 0.0337 0.0179 0.0000

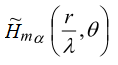
0 0.3420 0.6428 0.8660 0.9848 0.9848 0.8660 0.6428 0.3420 0.0000

0 0.1650 0.3101 0.4178 0.4751 0.4751 0.4178 0.3101 0.1650 0.0000

0 0.1092 0.2053 0.2766 0.3146 0.3146 0.2766 0.2053 0.1092 0.0000

0 0.0817 0.1536 0.2070 0.2353 0.2353 0.2070 0.1536 0.0817 0.0000

0 0.0653 0.1227 0.1654 0.1881 0.1881 0.1654 0.1227 0.0653 0.0000

0 0.0544 0.1022 0.1377 0.1566 0.1566 0.1377 0.1022 0.0544 0.0000

0 0.0466 0.0876 0.1180 0.1342 0.1342 0.1180 0.0876 0.0466 0.0000

0 0.0408 0.0766 0.1032 0.1174 0.1174 0.1032 0.0766 0.0408 0.0000

0 0.0362 0.0681 0.0917 0.1043 0.1043 0.0917 0.0681 0.0362 0.0000

0 0.0326 0.0613 0.0826 0.0939 0.0939 0.0826 0.0613 0.0326 0.0000

0 0.0296 0.0557 0.0751 0.0853 0.0853 0.0751 0.0557 0.0296 0.0000

0 0.0272 0.0511 0.0688 0.0782 0.0782 0.0688 0.0511 0.0272 0.0000

0 0.0251 0.0471 0.0635 0.0722 0.0722 0.0635 0.0471 0.0251 0.0000

0 0.0233 0.0438 0.0590 0.0670 0.0670 0.0590 0.0438 0.0233 0.0000

0 0.0217 0.0408 0.0550 0.0626 0.0626 0.0550 0.0408 0.0217 0.0000

0 0.0204 0.0383 0.0516 0.0587 0.0587 0.0516 0.0383 0.0204 0.0000

0 0.0192 0.0360 0.0486 0.0552 0.0552 0.0486 0.0360 0.0192 0.0000

0 0.0181 0.0340 0.0459 0.0521 0.0521 0.0459 0.0340 0.0181 0.0000

0 0.0172 0.0322 0.0434 0.0494 0.0494 0.0434 0.0322 0.0172 0.0000

0 0.0163 0.0306 0.0413 0.0469 0.0469 0.0413 0.0306 0.0163 0.0000

Функция MATLAB, которая выдала нам такие результаты и графики

function OtnAmp = OtnAmp()

Emr=zeros(20,19);

Emq=zeros(20,19);

Hma=zeros(20,19);

for i=1:20

r=.5*i;

for j=1:19

Q=(j*10-10)*pi/180;

Emr(i,j)=((.5/r)^3)*sqrt((1+4*(pi^2)*(r^2))/((1+4*(pi^2)*(.5^2))))*abs(cos(Q));

Emq(i,j)=((.5/r)^3)*sqrt((1-4*(pi^2)*(r^2) + 16*(pi^4)*(r^4))/(1-4*(pi^2)*(.5^2)+16*(pi^4)*(.5^4)))*sin(Q);

Hma(i,j)=((.5/r)^2)*sqrt((1+4*(pi^2)*(r^2))/((1+4*(pi^2)*(.5^2))))*sin(Q);

end

end

Emr

Ema

Hma

plot ([Emr(:,6) Emq(:,6) Hma(:,6)])

end

1 А.Н. Коваленко, А.Н. Щербицкий «Электродинамика и распространение радиоволн», ч.1, стр. 32

2 Исаков В.Н., Коваленко А.Н. «Электродинамика и распространение радиоволн: методические указания по выполнению лабораторных работ» МИРЭА 2011

3 На графике на оси ординат – составляющие амплитуд, на оси абсцисс – отношение r/λ, умноженное на 2.

4 А.Н. Коваленко, А.Н. Щербицкий «Электродинамика и распространение радиоволн», ч.1, стр. 68

5 А.Н. Коваленко, А.Н. Щербицкий «Электродинамика и распространение радиоволн», ч.1, стр. 54

18