МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Московский государственный технический университет радиотехники, электроники и автоматики" МГТУ МИРЭА
__________________________________Кибернетика________________________________ (наименование факультета)
____________________________ «Высшая математика»_____________________________ (наименование кафедры)

КУРСОВАЯ РАБОТА
по дисциплине
«_____________________Спецкурс №3____________________» (наименование дисциплины)
Тема курсовой работы «Расчет характеристик электромагнитного поля элементарного электрического излучателя» (наименование темы)
Студент группы ____________________ (учебная группа)	_______________________________________________ (Фамилия И.О)
Руководитель курсовой работы (должность, звание, ученая степень)	_______________________________________ (Фамилия И.О)
Рецензент (при наличии) __________________________________________ (должность, звание, ученая степень)	_______________________________________ (Фамилия И.О)

Работа представлена к защите	«__»_______201___ г.	(подпись студента)
«Допущен к защите»	«__»_______201___ г.	(подпись руководителя)

Москва 2012

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Московский государственный технический университет радиотехники, электроники и автоматики" МГТУ МИРЭА
____________________________Кибернетика__________________________________ (наименование факультета)
_________________________ «Высшая математика»_____________________________ (наименование кафедры)
			Утверждаю
			Заведующий кафедрой_______________Ю.И.Худак
			(Ф.И.О.) «____» __________201___ г.
ЗАДАНИЕ
на выполнение курсовой работы
по дисциплине «_______________Спецкурс №3_________________________________»
Студент ____Анташкевич А.А.______________________Группа__КБ-31-08____
Тема«Расчет характеристик электромагнитного поля элементарного электрического излучателя»
Исходные данные: 1)Расположение излучателя в пространстве r 2)Сторонний ток в излучателе Iст 3)Длина излучателя l 4) Длина волны λ
Перечень вопросов, подлежащих разработке, и обязательного графического материала: 1)Вывод формул основных характеристик ЭМ-поля 2)Зависимости относительных амплитуд составляющих векторов поля от отношения r/λ, меняющемся от 0.5 до 10 3)Определение расстояния, на котором погрешность формулы для дальней зоны меньше 1% 4) Диаграммы направленности в различных плоскостях. Графический материал: 1) Зависимости относительных амплитуд от отношения r/ λ 2) Диаграммы направленности
Срок представления к защите курсовой работы: до «___» ________________201_ г.
Задание на курсовой проект, (работу) выдал		«___»______201__г.		_____________________________ Подпись руководителя проекта		___________________________ Ф.И.О. руководителя проекта
Задание на курсовой проект, (работу) получил		«___»______201__г.		_____________________________ Подпись студента –исполнителя проекта		___________________________ Ф.И.О. студента -исполнителя проекта

Содержание

Введение … 4

Теоретическая справка, вывод формул … 5

Практическая часть, математические расчеты … 8

Диаграммы направленности … 9

Заключение … 15

Список литературы … 16

Приложение … 17

Введение

Цель данной курсовой работы - изучить, как ведет себя электромагнитной поле элементарного электрического излучателя. Посмотреть, как быстро оно убывает и насколько точны формулы для дальней зоны, которые намного проще универсальных формул для любой точки. Математические расчеты были выполнены в программе MATLAB, текст функции и наиболее громоздкие таблицы приведены в приложении.

Теоретическая справка

Векторный потенциал

Элементарный электрический излучатель – это короткий отрезок тонкого провода, по которому течёт электрический ток с постоянной амплитудой и фазой. При этом длина провода l много меньше расстояния r до точки, в которой определятся поле, и много меньше длины волны , где - коэффициент фазы, а радиус провода a много меньше его длины l. Комплексная амплитуда стороннего тока в каждой точке излучателя является постоянной величиной. Таким образом, условия элементарности можно записать в виде:

а) l<<r; б) l<< ; в) а<<l; г) =const.

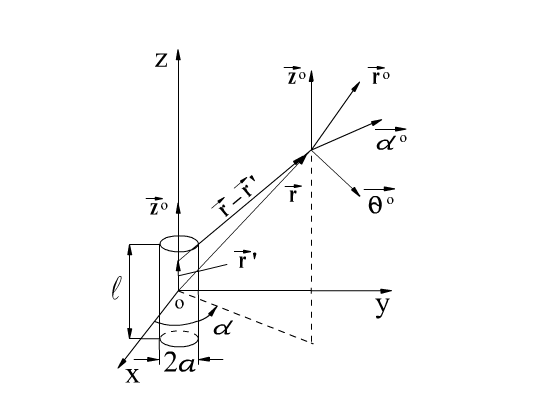
Рассматривая элементарный излучатель как прямолинейный отрезок линейного тока и используя выражение для векторного потенциала линейного тока¹:

.

, представим векторный потенциал в виде:

Где - радиус-вектор, проведённый из начала координат в произвольную точку излучателя на оси z:

Распишем подынтегральный модуль в виде корня:

|r – r’|= √(x-x’)² +(y-y’)² +(z-z’)²

В силу элементарности излучателя, имеем x’=0 и y’=0:

|r – r’|= √x² +y² +(z-z’)²

Так же заметим, что при условии l<<r выражение z-z’ будет мало меняться. Так что можно пренебречь и значением z’, положив его равным 0. Итак, получаем |r-r’|= √x² +y² +z² = r

Напряженность поля

Напряжённость магнитного поля находим, используя формулу и представление в сферической системе координат ( ):

,

где - орты сферической системы координат.

Векторный потенциал представляем в виде разложения по этим ортам: , (2.52)

где ;

Раскрывая определитель (2.51) по элементам первой строки, получим следующее выражение для комплексной амплитуды напряжённости магнитного поля:

Используя первое уравнение электродинамики для комплексных амплитуд, можно получить следующее выражение для комплексной амплитуды напряжённости электрического поля: .

Из последнего выражения следует, что вектор напряженности электрического поля ЭЭИ имеет две составляющие – радиальную и меридиональную, а вектор напряженности магнитного поля – только азимутальную.

Назовем относительной амплитудой отношение составляющих векторов поля при r=r к соответствующим значениям при r=r_н.

Использую последние формулы для расчета H_m и E_m, получим соответствующие формулы относительных амплитуд для трёх составляющих²: