19 Билет

1. Особенности работы следящей системы с двухканальной схемой измерения рассогласования на сельсинах.

?

2 вопрос. Среднее время безотказной работы изделия. Связь с другими характеристиками надежности

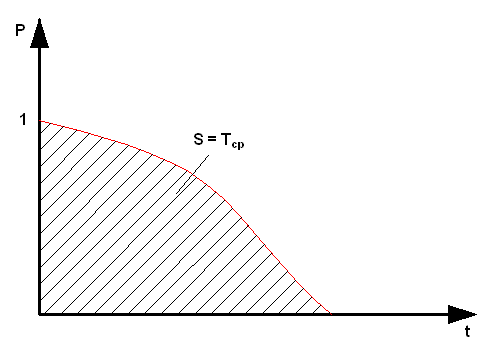
По определению – это математическое ожидание времени работы изделия до первого отказа.

Т – случ. величина – время работы изделия до первого отказа. Данная величина может принимать значение 0 < t < ∞.

Известна a(t) – плотность распределения случ. величины Т.

T_ср = M [T] = m_T =

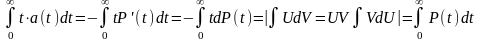
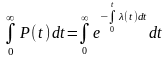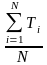Тогда T_ср = Оценка статистическая T^ст_ср = , Где N – число изделий, работа которых рассматривается до первого отказа. Т_i – время работы i – того изделия до первого отказа.

20 Билет

1 Синхронное детектирование амплитудно-модулированных сигналов

Амплитудным детектором (АД) называется устройство, предназначенное для получения на выходе напряжения, изменяющегося в соответствии с законом модуляции амплитуды входного гармонического сигнала. Процесс детектирования амплитудно-модулированных (АМ) сигналов вида

u_c (t)  u_a(t)cos(ω_ct), (1)

где u_a(t)U_c[1m_ax(t)], m_a  1 – коэффициент глубины модуляции; U_c – амплитуда несущего колебания с частотой ω_c, заключается в воспроизведении модулирующего сообщения x(t) с наименьшими искажениями. Спектр сообщения x(t) сосредоточен в области низких частот (частот модуляции), а спектр сигнала u_c (t) – в области частоты ω_c, значение которой обычно намного превышает значение наивысшей частоты модуляции.

В качестве синхронного детектора обычно используется аналоговый перемножитель сигналов. При этом на один из входов аналогового перемножителя поступает амплитудно-модулированный сигнал u_c(t) (1), на другой вход – опорное когерентное колебание u₀(t). В результате перемножения колебаний на выходе образуются низкочастотная составляющая 0,5u_a(t)U₀ и высокочастотная составляющая 0,5u_a(t)U₀cos(2_ct), которая устраняется на выходе с помощью фильтра низкой частоты C_нR_н. К основным преимуществам синхронного детектора относятся:

• малые нелинейные искажения u_вых(t), вследствие работы при достаточно больших напряжениях опорного колебания в режиме детектирования «сильных» сигналов;

• возможность подключения в качестве нагрузки ФНЧ с полосой прозрачности, величина которой не зависит от значений частоты _max модулирующего колебания;

• высокое входное и низкое выходное сопротивления, что обеспечивает хорошее согласование с соседними каскадами устройств обработки сигналов.

Однако преимущества синхронного детектирования амплитудно-модулированных сигналов реализуются лишь при точной синхронизации опорного и несущего колебаний. В реальных устройствах возможен фазовый сдвиг  между указанными колебаниями, вызванный задержкой в цепи формирования опорного колебания.

При наличии фазового сдвига   0 амплитуда колебания на выходе синхронного детектора будет равна:

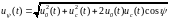
Разлагая в степенной ряд и ограничиваясь первыми членами разложения, можно получить: .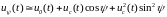

Если входной сигнал u(t) имеет амплитудную модуляцию вида u_a(t)=U_c[1+m_acosΩt], то полезный сигнал на выходе синхронного детектора (без учета коэффициентов усиления) имеет вид: u_вых(t)=0,5U_c[1+m_acosΩt]U₀cos.

Из выражения (22) следует, что максимальное значения u_вых(t) достигается при величине   2k, что и следовало ожидать.

2 Расчет надежности системы при основном ( последовательном) соединении её элементов.

Пусть система включает в себя N элементов, соединенных с точки зрения надежности, последовательно.

1 эл-т

i эл-т

N эл-т

_N(t)

_i(t)

₁(t)

Известны интенсивности отказов этих элементов. Будем считать, что отказы элементов в системе события случайные, независимые, по форме проявления внезапные.

Требуется определить: Р_(сист) (t), T_{ср сист} (t).

Обозначим событие А_i – это безотказная работа элемента i в интервале 0…t

Вероятность осуществления этого события: 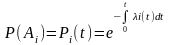Таких событий i=1…N

Событие А – сложное событие, заключающее в совместном осуществлении всех событий А_i .

Такое событие обозначается как произведение:

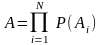
Вероятность осуществления этого события: 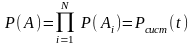вероятность безотказной работы системы

Тогда: 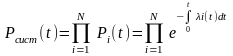Частный случай _I(t)=_I=const, I Тогда

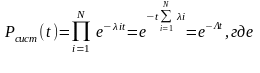
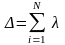_i суммарная интенсивность отказов в системе, то есть эта величина постоянная, то для системы мы также будем иметь экспонециальный закон надежности. 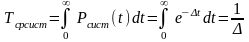В литературе можно встретить следующую формулу: 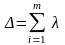_IN_i , где m-число типов элементов в системе, N_i –число элементов i-ого типа.

При расчете надежности системы следует учитывать условия эксплуатации системы с помощью различных поправочных коэффициентов, вводимых для интенсивности отказов. В таблицах книг по надежности даются интенсивности отказов.

_i0 – для нормальных (лабораторных) условий работы, где считается, что t⁰C=20⁰C,

P=760 мм рт. ст., =60% Отсутствуют удары, вибрации и др. вредные внешние воздействия.

При отличий работы от указанных вводятся поправки на интенсивности отказов.

В литературе имеется много графиков поправок, учитывающих влияние на надежности температуры в зоне шасси прибора и коэффициента нагрузки элемента.

Эти поправки имеют вид: Поправочный коэффициент

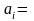
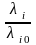
К_н=1

К_н=0,9

К_н – коэффициент нагрузки элемента

а_i

К_н=0,8

К_н=0,7

t⁰C

температура зоны шасси прибора

Коэффициент нагрузки в общем случае:

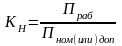
Обычно берется тот физический параметр, который в большей степени влияет на надежность.

Например для резистора таким параметром является рассеиваемая на нем мощность 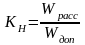Рекомендуется для резисторов выбирать К_н0,5

Для конденсаторов определяющим фактором является напряжение на обкладках конденсатора:

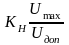
Для контактов (реле, разъемы) определяющим фактором является ток, протекающий через них: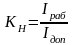

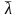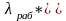Хуже исследовано влияние таких факторов как удары, вибрации, агрессивность сред и т.д на надежность изделия. Предлагается совокупность всех неучтенных факторов учитывать коэффициентом назначения аппаратуры, так что: _раб= К_{назначения} В литературе можно встретить: