§ 3.4. Гидравлические регуляторы

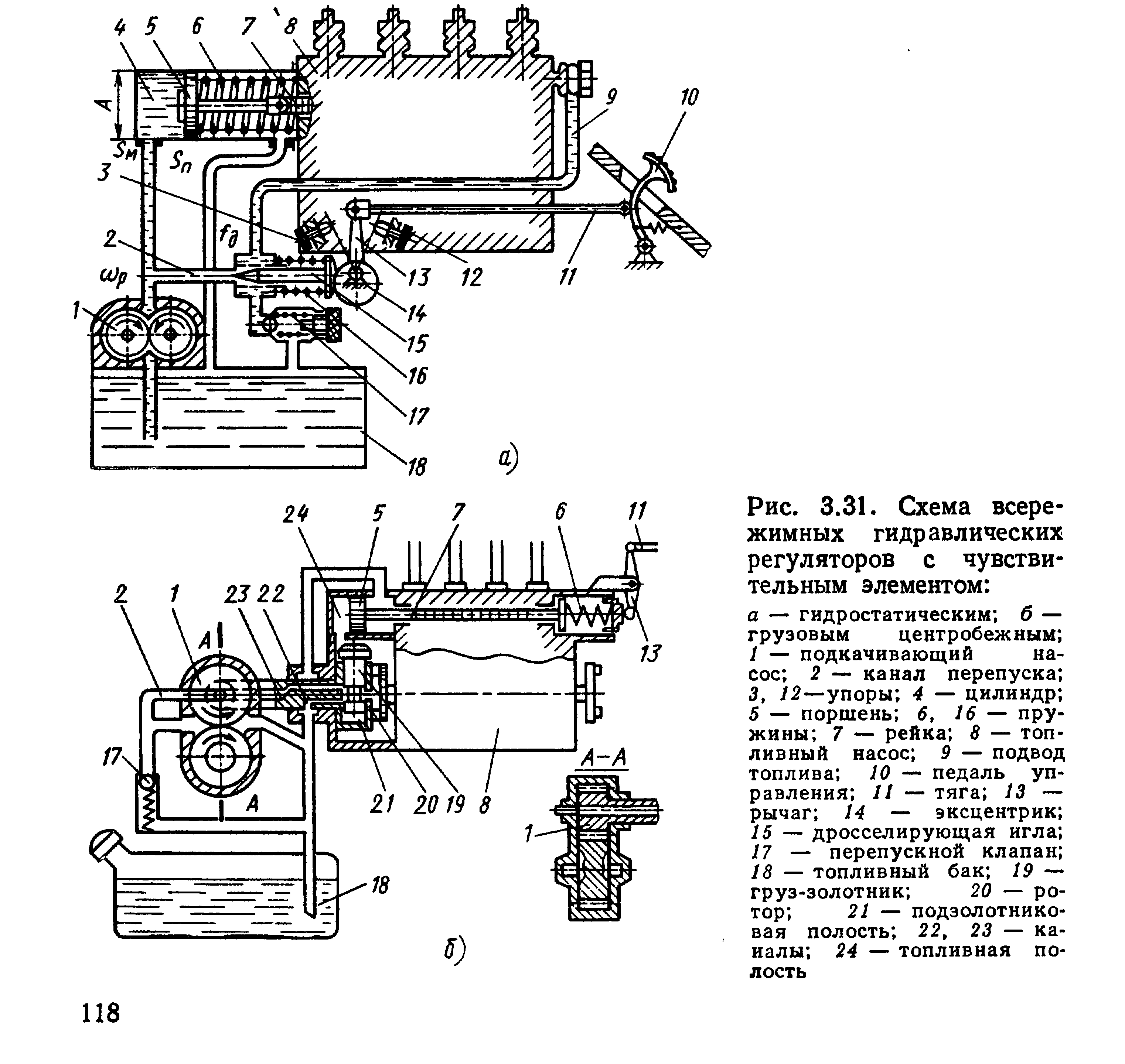
Принцип действия. В гидравлическом регуляторе пря­мого действия (рис. 3.31, а) в качестве рабочего тела может быть использовано машинное масло или топливо. Топливо насосом 1 подается в цилиндр 4. Избыток его через дросселирующую иглу 15 и перепускной клапан 17 сливается в бак 18.

В цилиндре 4 расположен поршень 5, связанный с рейкой 7 топливного насоса 8. Его положение обусловливается равенством

сил, создаваемых с одной стороны пружиной 6, с другой — дав­лением топлива в левой полости цилиндра 4. При возрастании угловой скорости вала двигателя усиливается подача топлива насосом 1, что влечет за собой увеличение давления в цилиндре 4 и перемещение поршня 5 вместе с рейкой 7 в сторону уменьшения подачи топлива. Всережимность регулятора может быть обеспе­чена перестановкой иглы 15 рычагом 13 и педалью 10 управле­ния или изменением предварительной деформации пружины 6.

Восстанавливающая и поддерживающая силы. Восстанавли­вающая сила гидравлических регуляторов определяется усилием пружины 6 (рис. 3.31, а). Если Е₀ — усилие предварительной де­формации, то

Е = Е₀ + Ьг, (3.73)

где Ь — жесткость пружины.

Если всережимность обеспечивается изменением предвари­тельной деформации пружины, то Е₀ = / (чр), где \|э — положение органа управления, и тогда в соответствии с формулой (3.73) Е = / (г; ф), что графически может быть представлено сеткой прямых Е — / (г) при \|>_г = сопз* (характеристики 2—6 на рис. 3.32).

Поддерживающая сила в гидростатических чувствительных элементах определяется избыточным давлением топлива р, вос­принимаемым площадью /_п поршня 5 (см. рис. 3.31, а). Следова­тельно,

Л<о* = /„/>. (3.74)

Избыточное давление р топлива создается топливным насосом, секундная производительность которого О_с =

5 — площадь поперечного сечения впадины между зубьями зуб­чатых колес насоса; Ь_х — длина зуба; 1_г — число зубьев; Т1_Н — коэффициент подачи насоса; — угловая скорость зубчатых колес; р — плотность топлива. Если ц,_р/ — эффективное проход­ное сечение регулировочного отверстия, то количество топлива, проходящее через это отверстие в секунду, С_е = ц_р/ 7/ 2рр. Так как производительность 0_С насоса при равновесном режиме равна расходу 6₀ топлива через регулировочное сечение, то

р — С0р/[2(ц_н/) ]. (3.75)

Таким образом,

Лео р = {р/_п/[2 (Цр/)²]) (5Ь_г1_гт)н/я)² сор. (3.76)

Это соотношение показывает, что в гидростатических чувстви­тельных элементах поддерживающаяся сила при постоянном по­ложении рычага управления (задано Цр/) определяется конструк­цией чувствительного элемента, плотностью и вязкостью топлива, а следовательно, и его температурой и не зависит от положения муфты регулятора (кривая 1 на рис. 3.32). Наличие характеристик восстанавливающей и поддерживающей сил дает возможность построения статической характеристики гидравлического регуля­тора (кривые 7—9 на рис. 3.32). Каждой характеристике восста­навливающей силы Е = / (г) при \|> = сопз1 соответствует своя статическая характеристика регулятора г = / (со_р) при г|> = сопз1.

Следует отметить, что зависимость поддерживающей силы от температуры рабочей жидкости является существенным недостат­ком гидравлического чувствительного элемента такого типа, свя­занным с нарушением первоначальной настройки скоростного ре­жима вследствие изменения вязкости и плотности рабочей жидко­сти, используемой для регулирования, при изменении ее темпе­ратуры в процессе эксплуатации или при замене одного сорта топлива другим.

Гидравлический регулятор прямого действия с грузом-золот­ником. Чтобы устранить указанный выше недостаток гидравли­ческого чувствительного элемента, в гидравлических всережимных регуляторах применен грузовой центробежный чувствительный элемент (с грузом-золотником) 19 (рис. 3.31, б), который может свободно перемещаться в радиальном направлении сверления ротора 20. Центр тяжести груза-золотника 19 смещен относи­тельно оси вращения ротора. Топливо насосом 1 подается в ка­нал 22, давление в котором зависит от настройки перепускного клапана 17. Из канала 22 через выточки в грузе-золотнике 19 топливо поступает в полость 24. Изменение давления топлива вос­принимается поршнем 5 и пружиной 6. Вместе с поршнем пере­мещается рейка 7 топливного насоса 5, изменяющая подачу топ­лива.

Всережимность регулятора обеспечивается изменением с по­мощью рычага 13 предварительной деформации пружины 6. Дав­ление топлива в полости 24 определяется положением груза- золотника и, следовательно, площадями проходных сечений ка­налов 22 и 23. В процессе работы центробежная сила груза- золотника уравновешивается силой, создаваемой избыточным дав­лением р в полости 24. Эта особенность регулятора практически исключает зависимость поддерживающей силы регулятора от вязкости топлива и, следовательно, его температуры, что исправ­ляет указанный выше недостаток гидравлических чувствительных элементов. Однако введение в конструкцию регулятора груза- золотника 19 (см. рис. 3.31, б) повышает сложность конструкции по сравнению с регулятором, показанным на рис. 3.31, а.

Статический расчет всережимного гидравлического регулятора. Поршень 5 регулятора непосредственно связан с рейкой топлив­ного насоса, поэтому значение восстанавливающей силы опреде­ляется по формуле (3.20) при н_р = 1. Из условия статического равновесия на номинальном режиме (Е_пом == Лсор _НОм) находят диаметр поршня & = Е_вои/(пр_вогл). Давление топлива р_т за дросселирующей иглой 15 (см. рис. 3.31, а) обеспечивается уста­новкой перепускного клапана 17 и составляет обычно 0,15— 0,2 МПа. Давление р перед дросселирующей иглой в цилиндре 4 должно быть выше на Др = (0,1-ь0,2) МПа.

После оценки р_ном и р_т в соответствии с формулой (3.75) можно определить дросселирующее сечение /_тах, создаваемое иглой 15 при установке рычага управления 13 на упор 3:

/шах ⁼⁼ «5&₂/₂Т|_н(0р номР/ЕН'рЯ' V 2р (рном Рт)]» где коэффициент подачи насоса г|_н = 0,65-г-0,71.

Знание /_шах дает возможность построить зависимость избы­точного давления от угловой скорости со_р регулятора (кривая 10 на рис. 3.32). Точка А соответствует номинальному режиму работы двигателя, при котором рейка топливного насоса нахо­дится в положении полной подачи топлива. После выбора степени неравномерности на номинальном режиме 6_Н0М по формуле

со — ² + дном

Юр шях — Юр ^ном 2 — бном

определяют максимальную угловую скорость регулятора. Пер­пендикуляр к абсциссе со_{р тах} дает точку В холостого хода на регуляторной характеристике 12 и максимальное значение избы­точного давления рабочей жидкости р_тах.

Так как минимальная угловая скорость со_{р т1п} минимального скоростного режима известна, то при р = р_н6м определяют точку С и по формуле

/ш1п = 8Ь_г(0р т1п*2^Т1нР/[Н'рЯ V 2р (Рвом — Рт)]

находят минимальное дросселирующее сечение, устанавливаемое иглой 15 (см. рис. 3.31, а). После того как выбраны размеры и форма дросселирующей иглы 15, по значению /_т1„ устанавливают упор 12. При / = }_т1п по формуле (3.75) с учетом противодавления р_г строят кривую 11 (см. рис. 3.32), которая является левой границей области работы регулятора (СО соответствует регуляторной характеристике 13). Регулирование промежуточных скоростных режимов обеспечивается установкой педали управления в про­межуточные положения между упорами 3 и 12 (см. рис. 3.31, а).

Степень неравномерности гидравлического регулятора, как и пневматического, не зависит от скоростного режима, если все- режимность обеспечивается иглой 15 (см. рис. 3.31, а), а не изме­нением предварительной деформации пружины 6.

Зная р_шах и /„ поршня регуляторов, можно определить макси­мальное значение восстанавливающей силы Е_тах — рпих/п и же­сткость пружины Ь = (Ешах — Е_вои)/АН.

Дифференциальное уравнение всережимного гидравлического регулятора. Уравнение динамического равновесия гидравличе­ского чувствительного элемента, написанное в соответствии с прин­ципом Даламбера, имеет вид

ц (й² Дг/сЙ²) + •& (й Аг/сИ) + АЕ = /_п А р. (3.77)

Предварительная деформация пружины чувствительного эле­мента постоянна, поэтому

АЕ = №/&) Аг. (3.78)

Поддерживающая сила (3.76) не зависит от положения г поршня 5 чувствительного элемента, поэтому

Р_р = йЕ/йг.

Давление в камере чувствительного элемента р или р = / (<о_р; гр), где ф — координата положения На основании этого

Ар = «ц, (др/дсо_р) До + (др/дхр) Дг|), (3.80)

где и_т — передаточное отношение от вала двигателя к подкачи­вающему насосу. С учетом выражений (3.78)—(3.80) уравнение (3.77) примет вид

ц (й²Аг/сИ²) + Ф (йАг/сИ) + Р_рАг = 2и²_тА(аА(о + /„ (др/д^р) Дф. (3.81)

Если ввести относительные отклонения от положения равно­весия и учесть, что в положении статического равновесия Е₀ = — и^А соо> то деление всех членов уравнения на коэффициент при <р приводит уравнение гидравлического регулятора к виду (3.43) или (3.44) с собственным оператором (3.45). Коэффициент настройки режима работы регулятора

9_Р = (/,Ж№) (дрЩ).

Приведенный вывод дифференциального уравнения гидравли­ческого чувствительного элемента справедлив при отсутствии разрыва сплошности жидкости и явлений кавитации, возникнове­ние которых в рассматриваемых системах маловероятно из-зг небольших движущихся масс и сравнительно высокого давления рабочей жидкости на установившихся режимах.

Деление всех членов уравнения (3.44) на собственный оператор позволяет получить уравнение (3.46) и построить структурную схему (см. рис. 3.26, а).