Глава 5

ДВУХИМПУЛЬСНЫЕ АВТОМАТИЧЕСКИЕ РЕГУЛЯТОРЫ

§ 5.1. Двухимпульсные регуляторы по скорости и ускорению

Анализ возможностей различных принципов регули­рования (см. §2.11) показал определенные преимущества каж­дого из них. Однако способность обеспечивать устойчивость ра­боты при различных свойствах регулируемого объекта имеет только принцип Ползунова — Уатта. Стремление использовать в САР преимущества различных принципов регулирования при­вело к созданию двухимпульсных* регуляторов.

В автоматических регуляторах двигателей применяют двух- импульсные регуляторы, работающие в соответствии с принци­пами Ползунова — Уатта и братьев Сименс. Они реагируют не только на изменение угловой скорости, но и на изменение угло­вого ускорения. Такой эффект может быть получен, если в чув­ствительном элементе, показанном на рис. 3.1, д, выполнить пазы, в которых располагаются грузы, не радиально, как в схеме на рис. 3.1, д_у ас определенным наклоном под углом а (рис. 5.1). При появлении ускорения (например, в сторону увеличения ча­стоты вращения) скошенные пазы траверсы 2 воздействуют на грузы 1, имеющие инерционность, таким образом, что перемещают их в сторону увеличения радиуса вращения. Муфта 5 получает при этом перемещение вправо, уменьшая подачу топлива. В таком чувствительном элементе появляются две дополнительные силы:

• действующие по касательной к окружности вращения тан­генциальные инерционные силы шаров

Л = ТЩаГ (Жй_р/<И),

где т_ш — масса шаров; г — радиус вращения шара;

• .сила взаимодействия грузов 1 с конической тарелкой 3, определяемая значением момента инерции /_м опорного диска муфты 5 регулятора:

Р_и — (У_м/г)(йсОрДй).

(5.1)

(5.2)

Термин «двухимпульсный» неточен и применен здесь как традиционный. В действительности под этим термином подразумевается регулятор, чувствитель­ный элемент (чувствительные элементы) которого воспринимает изменения двух входных координат, отражающих состояние регулируемого объекта.

Если й1 — расстояние, на которое перемещается шар вдоль паза, а йг — увеличение его радиуса вращения, то условие при­ведения сил (5.1) и (5.2) к оси движения муфты регулятора примет вид

(Р_г + Р_м) А1 соз (90° - ос) = Р_пр 0г,

где Р_пр — сила, приведенная к муфте; йг — перемещение муфты регулятора.

Так как й1 = йг/соз а и йг = р, то

Лх_Р==^(Жо_рА*0, (5.3)

где инерционный коэффициент чувствительного элемента по уско­рению

А} = Оп/ + Л./0 аДе Р- (5-4)

Таким образом, коэффициент А определяется не только массой шаров т_т и конструкцией чувствительного элемента (г, а и Р), но и моментом инерции муфты. Поэтому масса упорного диска 16 на рис. 3.19,а значительно увеличена.

Уравнение динамического равновесия двухимпульсного чув­ствительного элемента (см. рис. 5.1), написанное в соответствии с принципом Даламбера, имеет вид

\кй²^г/(И² + Ыкг/И + АЕ = Д (Лсор) + Д (Л/йш_р/Л). (5.5)

Так как на равновесном режиме йа>_р/й/ = 0, то Д (А^(о_р/сИ) = А; (АсОр/сИ).

Путем подстановки соотношений (3.27)—(3.29), (5.6) и пере­хода к относительным отклонениям переменных (3.31) уравне­ние (5.5) после деления всех членов уравнения на коэффициент при ф можно представить в виде

Т1(1²г\/сИ² + Г_КЛ)/Л + М = Т_гй у/(И + ср — 0_ра_р,

же

формулами, что и коэффициенты уравнения (3.33), а время Т_г, характеризующее эффективность воздействия на двухимпульс­ный чувствительный элемент углового ускорения, формулой

Т_Г = А^₀и_р/(2Е₀).

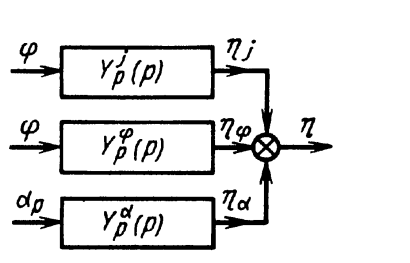
Рис. 5.2. Структурная схема двухимпульсного регулятора по скоростей ускорению

В операторной форме уравнение (5.7) имеет вид

(р) Л = «_Р (?) Ф ~ 0р«р. (5-9) где (р) — собственный оператор чувствительного элемента, определяемой формулой (3.45); опе­ратор воздействия по угловой скорости

и_р{р) = Т_гр + 1. (5.10)

Разделим все члены уравнения (5.9) на собственный оператор п = ^рО)ф + ^р(р)ф + Ур(р)<*р>

где передаточные функции двухимпульсного регулятора

VI о7) = (ТгР + \)1{т1р² + Т_кр + б_г);

У% (/О = 1/(Т²_рр² + Т_кр + б,); (5.11)

У Р (р) = - вр/(ту + т_кр + б_г).

В результате получим структурную схему, приведенную на рис. 5.2.