7.Как связаны между собой метод Фибоначчи и метод золотого сечения?

Метод почти половинного деления требует на каждой итерации двух вычислений значений функции: в точках   и  . Имеются два схожих по идее, но более экономных метода, в которых каждая итерация требует только одного нового вычисления значения функции. Если основные вычислительные усилия на каждой итерации приходятся именно на вычисление значений функции (так, как правило, и бывает), то это приводит к ускорению вычислений примерно вдвое по сравнению с методом почти половинного деления.

Один из методов называется метод золотого сечения. В этом методе длины последовательных отрезков   должны давать одно и то же число  :

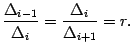
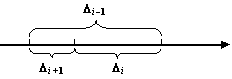
Рис.9.17.Три последовательных отрезка

При этом  , откуда легко получить, что число   удовлетворяет равенству  . Решая это уравнение, получаем, что 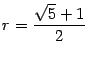 . Таким образом, на первом шаге на отрезке   вычисляются значения в двух точках   и  , расположенных симметрично на расстоянии   от концов отрезка   и   и делящих отрезок на части, составляющие "золотое сечение". Сравнивая точно так же, как в методе почти половинного деления, значения в этих точках, выбираем в качестве   либо  , либо  . Экономия по сравнению с методом почти половинного деления получается на всех остальных шагах, поскольку если процесс повторить на отрезке   при  , то одной из точек деления оказывается ранее найденная точка:   либо  , так что одно из двух значений функции найдено на предыдущей итерации.

Ещё один метод -- метод Фибоначчи -- применяется в тех случаях, когда заранее известно, сколько итераций мы собираемся совершить, и при этом хотим получить наибольшую возможную точность в определении точки минимума. При этом оказывается, что длины отрезков   связаны с последовательностью чисел Фибоначчи  , заданной начальными значениями   и рекуррентной формулой  .

8. В чем заключается достоинство метода золотого сечения?

Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале.

9. В чем заключается сущность аналитических методов оптимизации?

Группа аналитических методов оптимизации объединяет аналитический поиск экстремума функции, метод множителей Лагранжа,вариационные методы и принцип максимума. Аналитический поиск экстремума функции, заданных без ограничений на независимые переменные является наиболее простым, но применяется к задачам, у которых оптимизируемая функция имеет аналитическое выражение, дифференцируемое во всем диапазоне исследования, а число переменных невелико.

Аналитический метод оптимизации предусматривает аналитическое задание соответствующих функций и определение производных от них. В случае наличия таких ограничений, касающихся переменных величин, полезным может оказаться хорошо известный в математике метод множителей Лагранжа. 

Группа аналитических методов оптимизации объединяет аналитический поиск экстремума функций, заданных без ограничений, метод множителей Лагранжа, вариационные методы и принцип максимума. 

Для использования аналитических методов оптимизации необходимо, чтобы расчетная формула критерия, ограничения и связи между координатами, управлениями и независимой переменной, а также начальные и конечные условия были представлены в форме функций, которые могут быть по крайней мере один раз дифференцируемыми и могут иметь конечное число точек разрывов. 

Не отрицая значения аналитических методов оптимизации процесса бурения, авторы настоящей работы отдали предпочтение графо-аналитическим методам, тем более, что последние применительно к некоторым методам проводки стволов скважин больших диаметров не освещены в литературе. 

На основании изложенного можно заключить что разработка и усовершенствование аналитических методов оптимизации газовых сетей сохраняют свое значение. 

На основании изложенного можно заключить, что разработка и усовершенствование аналитических методов оптимизации газовых сетей сохраняют свое значение. 

В книге пятой настоящей серии Справочников ( в главе 6 первого раздела) излагаются основные математические методы решения экстремальных задач, лежащие в основе аналитических методов оптимизации. Поэтому в настоящей главе основное внимание уделено экспериментально-статистическим методам: оптимизации, а также вопросам применения методов к задачам управления в химической технологии. В связи с этим глава делится на две части.

Аналитические или классические ме­тоды оптимизации связаны с использованием возможностей и применением средств дифференциального и вариационного исчислений для определения экстремума функции це­ди. Эти методы позволяют определить точки, удовлетворяющие лишь необходимым признакам локальных экстремумов, для чего используются частные производные функции цели по параметрам. Поэтому применение классических методов возможно, только:

1. Если известно аналитическое выражение функции цели от параметров;

2. если эта функция дважды дифференцируема по параметрам.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.