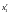1. Что такое «целевая функция»?

ЦЕЛЕВАЯ ФУНКЦИЯ [target function] в экстремальных задачах — функция, минимум или максимум которой требуется найти. Это ключевое понятие оптимального программирования. Найдяэкстремум Ц. ф. и, следовательно, определив значения управляемых переменных, которые к нему приводят, мы тем самым находим оптимальное решение задачи. Таким образом, Ц. ф. выступает как критерий оптимальности решения задачи.

Различается ряд видов Ц. ф.: линейная, нелинейная, выпуклая, квадратичная и др. — в соответствии с формой математической зависимости, которую они отображают. Следует также выделить термин “целевой функционал”: он применяется обычно, если Ц. ф. задачи является функцией от некоторых функций-ограничений.

2. Что такое «Текущий интервал неопределенности»?

Точки интервала неопределенности рассчитываются из правил золотого сечения. Алгоритм золотого сечения - это один из алгоритмов решения задач условной оптимизации одномерных унимодальных функций Ф(x) на интервале [a,b] методом сокращения текущего интервала неопределенности. Эти точки делят текущий интервал неопределенности на три подынтервала. На основе значений функции Ф(x) в указанных точках, один из указанных подынтервалов в силу унимодальности функции Ф(x) исключается из рассмотрения. Алгоритм относится к классу поисковых методов оптимизации.

Алгоритм золотого сечения относится к классу последовательных методов поиска:

1. Выполняем присваивания: , где

r – номер шага измерения,

ТИН – текущий интервал.

Для нашей задачи:

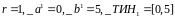
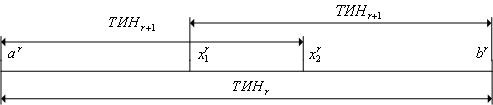
2. Вычисляем величины (см. Рис. 1)

=>для первого шага:

где, - постоянная «золотого сечения».

Рис. 1.  К определению величин x₁^r, x₂^r.

3. Вычисляем значения функции y в точках :

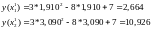
4. Если 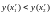, то выполняем присваивания .

Иначе - выполняем присваивания .

Очередной интервал задаём:

В нашем случае: , тогда: ,

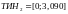
5. Если 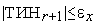, то заканчиваем вычисления. Иначе - выполняем присваивание 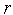= +1 и переходим на п.2. Здесь 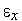– требуемая точность решения.

Для нашей задачи требуется не выполнение определенной точности вычисления, а выполнения восьми измерений, т.е. r=8.

Выведем все значения переменных в таблицу:

r	ar	br
1	0	5	1,90983	3,09017	2,663712	10,92609
2	0	3 ,09017	1,18034	1,90983	1,736888	2,663712
3	0	1,90983	0,72949	1,18034	2,760546	1,736888
4	0,72949	1,90983	1,18034	1,45898	1,736888	1,714028
5	1,18034	1,90983	1,45898	1,63119	1,714028	1,932822
6	1,18034	1,63119	1,352549	1,45898	1,667774	1,714028
7	1,18034	1,45898	1,286771	1,352549	1,673171	1,667774
8	1,286771	1,45898	1,352549	1,393202	1,667774	1,67742

(красным выделены те значения y, которые больше из двух y₁ и y₂).

Ответ: Минимум унимодальной функции y 1,668.