Глава 1. Факторы, определяющие фазовые переходы в атмосфере.

Система, пришедшая в фазовое равновесие, может находиться в нем без всяких видимых изменений до тех пор, пока внешние условия среды остаются постоянными.

1. Температура. Уравнение Клаузиса-Клайперона.

Для равновесия системы вода – пар или лед – пар требуется, чтобы в окружающей среде давление насыщения водяного пара соответствовала насыщению. Экспериментальным путем давно установлено, что давление насыщенного водяного пара резко возрастает с увеличением температуры. В дифференциальной форме эта зависимость, полученная на основании термодинамических соображений, выражается уравнением Клаузиуса- Клапейрона:

,

где L – теплота испарения,

E – давление насыщения водяного пара,

A – тепловой эквивалент работы,

R_п – удельная газовая постоянная для водяного пара,

T – температура.

Более строгий вывод приведенной зависимости можно получить, исходя из понятия термодинамического потенциала. Тогда мы имеем

dS = Aυdp – φdT.

Тогда условия равновесия двух фаз запишется в виде

,

или

Изменение энтропии в данном случае происходит вследствие затраты энергии на теплоту испарения, так что

.

Учитывая, что « , а следовательно, dυ ~ , и что р_п=Е соответствует давлению насыщенного пара, приходим к формуле (1)

.

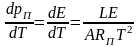Чтобы выражение для давления насыщенного пара в зависимости от температуры Е=f(T), следует проинтегрировать уравнение (1). За нижние пределы интегрирования возьмем Т₀=273 К и соответствующее ему значение Е₀=6,1078 мб. Тогда, считая в первом приближении L=const, получим

ln

Но так как

,

то

ln ,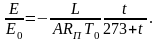

или

,

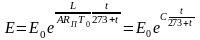где

.

Переходя к десятичному логарифму, имеем

.

Значения E(T), вычисленные по этой формуле, не совпадают точно с экспериментальными данными. На их основе была предложена эмпирическая формула Магнуса

Рассматривая вопрос о давлении насыщенного водяного пара над поверхностью капель, следует учесть влияние ряда факторов , к главнейшим из которых относятся:

1)кривизна поверхности, 2) наличие электрического заряда на капле и 3) присутствие в капле растворенных гигроскопических примесей.

Таким образом, давление насыщения пара над каплей является функцией нескольких переменных E=f(r,q,k,T).

За исходное значение примем давление насыщенного пара над плоской поверхностью (r=∞) дистиллированной воды. Обозначим эту величину через Е_∞. Тогда упругость пара над каплей Е при неизменной температуре можно записать в виде

Е= Е_∞+dЕ_r - dE_q – dE_p,

где dЕ_r- учитывает влияние кривизны поверхности,

dE_q – электрического заряда,

dE_p – концентрации раствора.

Рассмотрим зависимость Е от перечисленных факторов.