10. Признаки сравнения в общей и предельной формах.

Признак сравнения (в общей форме) Если для двух знакоположительных рядов и выполняется неравенство un vn для любых n , то:

1. из сходимости большего ряда следует сходимость меньшего ряда

2. из расходимости меньшего ряда ледует расходимость большего ряда

Признак сравнения (в предельной форме) Если для двух знакоположительных рядов и сущ-ет предел причем a≠0 a≠∞ , то оба ряда либо сходятся, либо расходятся.

11. Признаки Даламбера и Коши. Интегральный признак. Сходимость обобщенного гармонического ряда.

Признак Даламбера Если для знакоположительного ряда существует предел =D, то: 1) если D<1 , то ряд сходится; 2) если D>1, то ряд расходится;

3. если D=1, то это неопределенный случай.

Признак Коши Если для знакоположительного ряда существует предел k= то: 1) если k<1, то ряд сходится; 2) если k>1 , то ряд расходится;

3)если k=1, то это неопределенный случай.

Интегральный признак Функция f (x) , удовлетворяющая условию f( n)  , для любых n , называется производящей функцией ряда. Если знакоположительный ряд имеет монотонно убываю-щую производящую функцию f (x) на 1, , то:

1. из сходимости несобственного интеграла J= 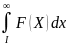следует сходимость ряда;

2. из расходимости несобственного интеграла J= следует расходимость ряда.

Исследовать на сходимость обобщенный гармонический ряд

12. Знакочередующиеся ряды. Признак Лейбница. Определения абсолютно и условно сходящихся рядов.

Определение. Ряды вида где все , называются знакочередующимися рядами.

Признак Лейбница (сходимости знакочередующегося ряда).

Пусть знакочередующийся ряд удовлетворяет условиям: 1) монотонно убывают 2)

Тогда ряд сходится, а его сумма S удовлетворяет неравенствам:S>0, S<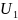

Признак абсолютной сходимости Если сходится ряд из модулей членов знакопеременного ряда 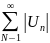то сходится и сам знакопеременный ряд сходится.

Определение. Знакопеременный ряд называется абсолютно схо- дящимся, если сходится ряд из модулей его членов.

Определение. Знакопеременный ряд называется условно сходя- щимся, если он сам сходится, а ряд из модулей его членов расходится.

13. Степенной ряд. Теорема Абеля. Интервал и радиус сходимости степенного ряда.

Степенным рядом называется ряд вида +…=

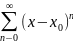
Вид области сходимости ряда вытекает из следующей теоремы.

Теорема Абеля/ Если степенной ряд +…сходится в точке x= , то он абсолютно сходится во всех точках, удовлетворяющих неравенству

2. Если степенной ряд расходится в точке x= , то он расходится во всех точках, удовлетворяющих неравенству

Интервал ( называется интервалом сходимости степенного ряда а число R называется радиусом сходимости ряда.

14. Схема нахождения области сходимости степенного ряда.

Дан степенной ряд

Эта задача решается по следующей схеме:

1)Составим ряд из модулей членов степенного ряда

2) К полученному знакоположительному ряду применим признак Даламбера (или Коши)

3) для нахождения области сходимости степенного ряда решаем неравенство

4) В результате решения неравенства получим интервал сходимости ряда.