
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Норми витрат сировини для виготовлення продукції
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
- •Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
Вп нуБіП України „Заліщицький аграрний коледж ім. Є.Храпливого”
Відділення Економічне
Спеціальність „Облік і аудит”
Форма навчання денна
Семестр VІ курс ІІІ, група 301
Дисципліна Економіко-математичне моделювання
ПАКЕТ ТЕСТОВИХ ЗАВДАНЬ
Варіант№10
Питання1. |
|
75 |
Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває |
1 |
на множині точок, що задовольняють всі обмеження |
2 |
в одній із вершин многокутника розв’язків |
3 |
в вершині многокутника |
4 |
на лініях, які обмежують многокутник розв’язків |
Питання 2. |
|
75 |
Причини виникнення ризику: |
1 |
зовнішні фактори ( зміна законодавства, інфляція, зміна податкової політики, зміна цін, конкуренція форс -мажор, корупція і рекет); |
2 |
внутрішні фактори; |
3 |
необов’язковість і безвідповідальність суб’єктів; |
4 |
усі відповіді вірні |
Питання 3. |
|
100 |
М
Для розв’язування симплекс методом скільки потрібно додаткових змінних? |
1 |
1 |
2 |
3 |
3 |
2 |
4 |
0 |
Питання 4. |
|
75 |
До позитивних якостей імітаційного моделювання можна віднести: |
1 |
всі висновки та твердження, зроблені на їх підставі мають евристичний характер і в певних випадках можуть суттєво викривляти дійсний стан речей; |
2 |
похибки, що об'єктивно притаманні моделям можуть істотно викривляти результати, отримані в ході імітаційного моделювання. |
3 |
усі відповіді вірні |
4 |
усі відповіді невірні |
Питання 5. |
|
|
У цільовій функції задачі лінійного програмування на max ( симплекс –метод) штучні змінні мають коефіцієнт |
1 |
+ М, де М — досить велике додатне число. |
2 |
- М, де М — досить велике додатне число |
3 |
+ М, де М — досить маленьке додатне число |
4 |
- М, де М — досить маленьке додатне число |
Питання 6. |
|
75 |
Для розв’язування ЗЛП симплекс методом необхідно, щоби |
1 |
одиничних векторів було стільки скільки обмежень в задачі |
2 |
одиничних векторів було більше ніж обмежень в задачі |
3 |
одиничних векторів було менше ніж обмежень в задачі |
4 |
одиничних векторів може бути довільна кількість |
Питання 7. |
|
|
Ризик – |
1 |
- це об’єктивно-суб’єктивна категорія, яка пов’язана з подоланням невизначеності, випадковості і конфліктності ситуації неминучого вибору й відображає ступінь досягнення очікуваного результату |
2 |
- це об’єктивно-суб’єктивна категорія, яка пов’язана з подоланням невизначеності очікуваного результату. |
3 |
- це об’єктивно-суб’єктивна категорія, яка пов’язана з подоланням невизначеності, випадковості очікуваного результату. |
4 |
-це об’єктивно-суб’єктивна категорія, яка пов’язана з подоланням невизначеності, випадковості і конфліктності ситуації неминучого вибору |
Питання 8. |
|
|
Вирази виду
|
1 |
Згорнений запис задачі лінійного програмування |
2 |
Згорнений запис задачі оптимізації |
3 |
Згорнений запис задачі математичного програмування |
4 |
Згорнений запис задачі цілочислового програмування |
Питання 9. |
|
|
Mатематична модель задачі лінійного програмування Z = x1 + 2x2 + 2x3 min; 2x1 + x2 - x3 =1 x1 + 2x2 + x3≥4 xj ≥0 j=1,2,3 Обмеження двоїстої задачі? |
1 |
2y1 + y2 =1 y1 + 2y2 ≥2 |
2 |
2y1 + y2 ≤1 y1 + 2y2 ≤2 -y1 + 2y2 ≤2 |
3 |
2y1 + y2 - y3 ≤1 y1 + 2x2 + x3≤2 |
4 |
2y1 + y2 ≥1 y1 + 2y2 ≥2 -y1 + 2y2 ≥2 |
Питання 10. |
|
|
План, утворений координатами вершини многогранника планів задачі |
1 |
допустимим планом задачі |
2 |
можливим планом задачі |
3 |
оптимальним планом задачі |
4 |
опорним планом задачі |
Завдання 2.
1.Сформулювати математичну модель даної задачі лінійного програмування.
2. Розв’язати дану модель в системі MicroSoft Excel, додаток Поиск решения.
3. Записати оптимальний план задачі і зробити їх економічний аналіз.
Задача. У цеху розрізують стальні прути завдовжки 6 м на заготівки 1,4; 2 і 2,5 м.
Усього в цеху мають 200 прутів.
Потрібно дістати не менше як 40, 60 і 50 заготівок завдовжки відповідно 1,4; 2 і 2,5 м.
Побудувати числову модель лінійного розкрою.
За критерій оптимізації - мінімум відходів.
Можливі варіанти розрізування
Довжина заготівки, м |
Варіанти розрізування прутів |
||||||
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
х7 |
|
1,4 |
4 |
— |
— |
1 |
1 |
2 |
2 |
2 |
— |
3 |
— |
1 |
2 |
1 |
— |
2,5 |
— |
— |
2 |
1 |
— |
1 |
1 |
Довжина відходів, м |
0,4 |
0 |
1 |
0,1 |
0,6 |
1,2 |
0,7 |

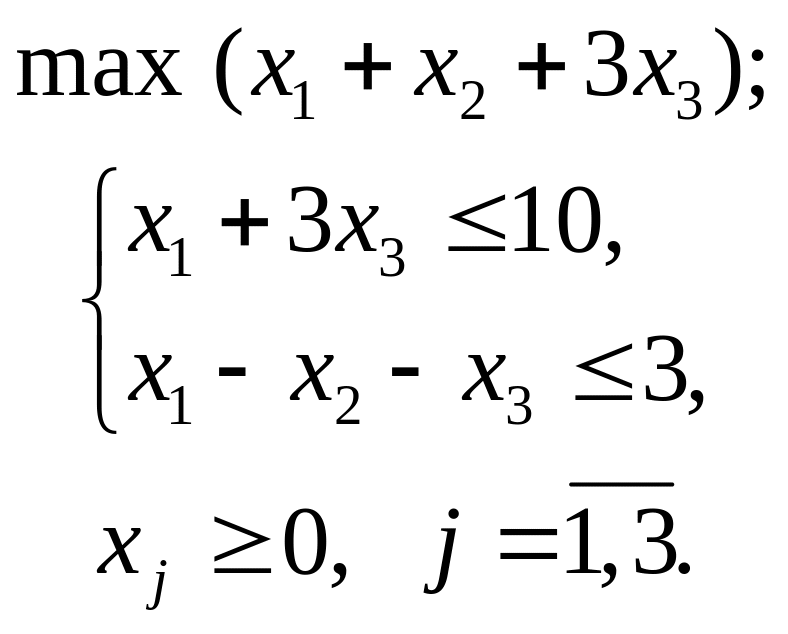 атематична
модель ЗЛП
атематична
модель ЗЛП
