23) Сущность и значение средней величины. Основные научные положения теории средней величины. Определяющее св-во средней

Средние величины – обобщающие характеристики изучаемого признака в совокупности. Средняя отражает типичный уровень величины признака для ед. совокупности в конкретных условиях места и времени. Средняя величина характеризует то общее, что есть в совокупности на основании вариации определенного признака.

Определяющее свойство средней: сумма или произведение индивидуальных значений признака равна сумме или произведению средних значений признака по объекту изучаемой совокупности. СВ является уравнительным значением признака для всех ед. совокупности. При исчислении средних по массе единиц влияние СВ взаимно погашается, а средняя дает возможность абстрагироваться от индивидуальных особенностей конкретных ед. и выражает общее св-во присущее все единицам.

Основным условием использования СВ является качественная однородность совокупности для которой рассчитана средняя. Средняя рассчитанная по совокупности – общая средняя, а для каждой группы – групповая средняя. Общая отражает то общее, что есть во всем явлении, а групповая – характерный размер явления, сложившегося в данной группе. Категории СВ: 1)степенные(алгебраические); 2)структурные(мода, медиана). Выбор вида и категории СВ зависит от цели исследования, экономической сущности усредняемого признака и характера исходных данных.

24) Средняя арифметическая, ее основные математические свойства и методы расчета

Средняя арифметическая – самый распространенный вид средней величины. Она исчисляется в тех случаях, когда объем усредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. Средняя арифметическая применяется в эконом. расчетах чаще других и при расчете используют ее свойства вытекающие из алгебраической формулы ее расчета:1) От уменьшения или увеличения всех вариантов усредняемой величины в А раз, их средняя соответственно уменьшится или увеличится в А раз 2) От уменьшения или увеличения веса каждого варианта в А раз, величина средней не меняется.3) Величина средней зависит не от абсолютных значений весов вариантов, а от пропорций между ними. 4) Если уменьшить или увеличить все варианты усредняемого признака на число А, то средняя уменьшится или увеличится на это же число А. Метод вычислений средней, основанный на этом свойстве, называется методом моментов, редукцией, отсчета от условного нуля. 5) Средняя величина умноженная на численность совокупности ( ) равна сумме произведений каждого варианта на его численность. 6) Сумма отклонений индивидуальных значений признака по средней арифметической равна 0 7) Сумма квадратов отклонений индивидуальных значений от их средней арифметической меньше, чем сумма квадратов отклонений индивидуальных значений от любой другой величины.

Е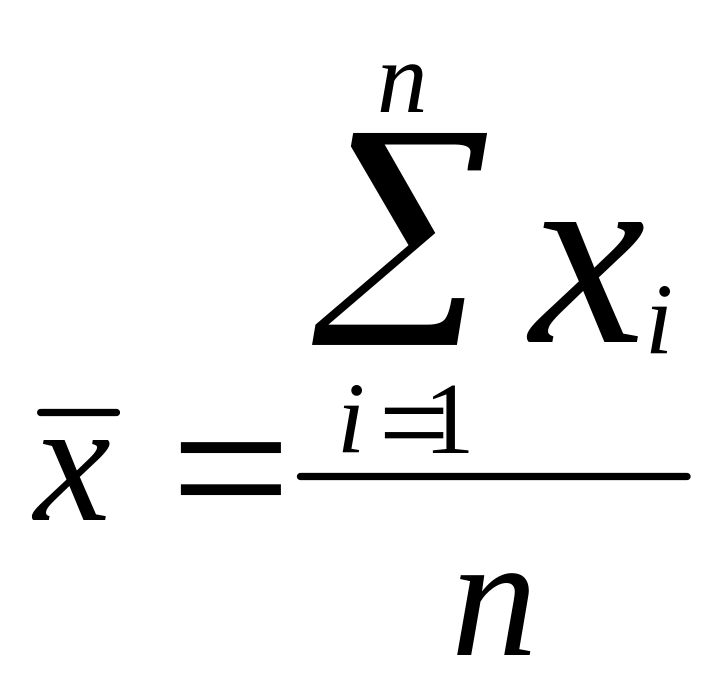 сли расчеты средней арифметической ведутся по вариац интервальным рядам, предварительно по каждой группе от интервальных значений признака в каждой группе переходит к дискретным выражениям путем определения полу-суммы, нижняя и верхняя границ интервального ряда. Первый открытый интервал при этом закрывается величиной (шириной) следующего за ним интервала, а последний открытый интервал закрывается величиной предыдущего интервала. Средняя арифметическая: взвешенная простая