49) Принципы построения многофакторных индексов

Индексный метод позволяет определить влияние не только двух, а любого числа факторов, формирующих сложное явление (результативный показатель). Если результативный фактор можно представить как последовательное произведение двух и более отдельных факторов, то такая связь называется мультипликативной. Например, производительность труда одного рабочего за месяц (среднемесячная выработка, у) равна его среднечасовой выработке (а), умноженной на среднее число отработанных часов за смену (среднюю продолжительность рабочего дня, b) и на среднее число отработанных за месяц дней (среднюю продолжительность рабочего месяца, с). Получаем следующую трехфакторную модель: .

А так как между индексами показателей существует такая же связь, как и между самими показателями, то Решение индексных мультипликативных моделей зависит от того, с какого фактора, экстенсивного или интенсивного, начинается произведение факторов-сомножителей в исследуемой модели:

а) если система взаимосвязи факторов начинается с интенсивного (качественного) показателя «а», то еще не рассмотренные факторы берутся на уровне отчетного периода, а уже рассмотренные остаются на уровне базисного периода.

б) если система взаимосвязи факторов начинается с экстенсивного (количественного) показателя «а», то еще не рассмотренные факторы берутся на уровне базисного периода, а уже рассмотренные – на уровне отчетного периода:

Чтобы определить абсолютное изменение результативного показателя в целом , нужно от числителя его индекса вычесть знаменатель: Общее абсолютное изменение результативного показателя равно сумме абсолютных изменений за счет влияния всех исследуемых факторов, формирующих это явление:

50) Территориальные индексы

Территориальные индексы характеризуют соотношение социально-экономических явлений в пространстве (по районам, областям).При построении агрегатной формы территориальных индексов возникает вопрос о том, какие показатели следует в этих индексах принимать в качестве весов или соизмерителей. При построении агрегатных территориальных индексов качественных показателей в качестве весов используют «стандартизированные веса». В качестве их можно, например, взять соответствующие количественные показатели по республике или стране, либо по двум сравниваемым территориям А и Б вместе (Q), гдеQ=q_a+q_b;

Произведение и =1, т.е.

Другим способом является сравнение индексируемого качественного показателя одной территории со средневзвешенной этого показателя по двум анализируемым территориям:

, , где

При Построение агрегатных территориальных индексов количественных показателей в качестве весов в зависимости от целей анализа, от поставленной экономической задачи берутся соответствующие средние показатели отдельных элементов, исчисленные либо по обоим сравниваемым территориям, либо по более широкой территории (области, республике). , ,

Косвенный метод

При этом методе формулы для расчета территориальных индексов качественных показателей, например, цены, имеют следующий вид:

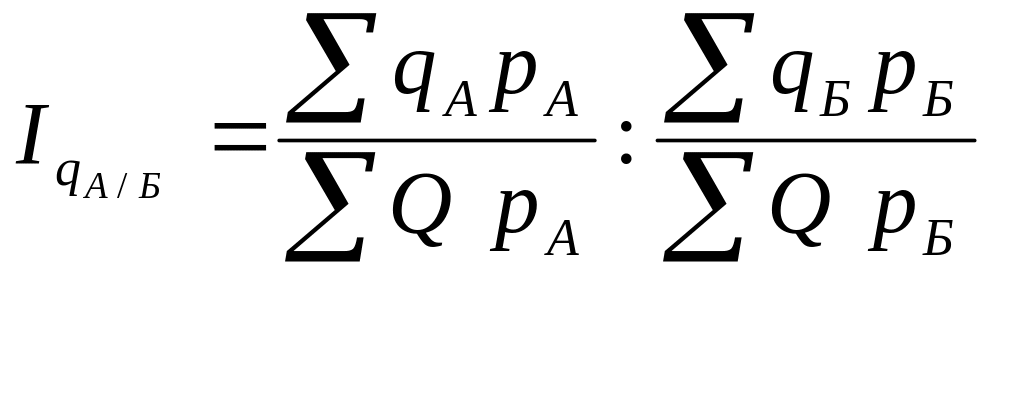и наоборот, а для расчета территориальных индексов количественных показателей, например, физического объема, такой вид: и наоборот где p и Q – стандартные значения.