41) Аналитическое выравнивание уровней ряда динамики. Уравнение тренда. Интерполяция, экстаполяция

Наиб.эффективн.способом выявления тенденции явл-ся аналитическое выравнивание, т.е.определение тренда. При этом уровне ряда динамики выражается в виде функции времени.Оно используется при изучении колебл.данных в динамике и связи изучаемых данных с др.явлениями.Оно состоит в подборе для данного ряда теоретической кривой,выраж.основные черты фактич. Динамики,т.е.целью явл-ся подбор такой теоретич.кривой,кот.наилучшим образом описывает эмпирич. данные,при этом исп-ся метод наименьших квадратов

∑ ; где t-условное обознач.времени, α-параметры искомой прямой. Основным содержанием метода аналитического выравнивания в динамических рядах является то, что закономерно изменяющийся уровень изучаемого экономического явления рассчитывается как функция времени (тренд): . Легкопроизводит.выравнивание по прямой,если t подобрать так,чтобы сумма t была=0,т.е.начало отсчета времени переносится в середину изуч.периода. Аналит.выравнивание ряда можно производить по параболе 2го порядка или более высоких степеней.При построении уравнения целью явл-ся определение модели развития явления во времени.Основанием для выбора формы прямой или кривой при выравнивании служит смысл изучаемого явления,кот.отражается рядом.Выравнивание по показат.функции применяется в практике,т.к.хар-тер динамики явления соответствует гипотезе о геометр.прогрессии.Изучение вариации имеет свою специфику в пределах однородной группы.Пределы вариации дают представления в тех границах,за кот.следует качеств.изменения.Существует норм.закон распределения,кот. Подчиняются естественные свойства данного явления и используются законы вариации средних величин.Вариация ср.величин меньше вариации индив.значений признака и позволяет оценить колеблемость более точно. Выравнивание по прямой применяется в тех случаях, когда характер движения изучаемого явления ближе всего к прямолинейному. При этом наблюдаются примерно равные постоянные цепные абсолютные приросты. Параметры а₀ и а₁ находятся путем решения следующей системы нормальных уравнений:

где y – фактические уровни ряда динамики; n – число уровней ряда; t – соответствующая нумерация фактора времени.

Эта система уравнений значительно упрощается, если значения времени подобрать так, чтобы их сумма равнялась нулю. Тогда:

;

Интерполяция - отыскание промежуточных значений величины по некоторым известным ее значениям. Напр., отыскание значений функции f(x) в точках x, лежащих между точками xo. Экстраполяция - нахождение уровней за пределами изучаемого ряда, т.е. продление ряда на основе выявленной закономерности изменения уровней в изучаемый отрезок времени.

42) Сезонные колебания и методы их изучения

При изучении месячных или квартальных уровней рядов динамики часто обнаруживаются постоянно повторяющиеся их колебания, существенно не изменяющиеся за длительный период времени. Такие изменения уровней ряда называют сезонными колебаниями. Для их выявления анализируются месячные или квартальные уровни динамического ряда за ряд лет. Характеристику сезонных колебаний производят с помощью индексов сезонности (IS). Способ определения индексов сезонности зависит от характера общей тенденции ряда динамики.

Если ряд динамики не содержит ярко выраженной тенденции в развитии, то изучение сезонности производят с помощью метода постоянной средней. Расчет индексов сезонности в таких рядах осуществляется по следующей формуле:

, где – осредненные эмпирические уровни ряда по одноименным периодам; – общий средний уровень ряда. Совокупность индексов сезонности, рассчитанных для каждого месяца годового цикла, характеризует сезонную волну развития явления во внутригодовой динамике.

Если в ряду динамики наблюдается ярко выраженная общая тенденция роста (снижения), то индексы сезонности определяются на основе методов, позволяющих исключить влияние данной тенденции. Так, индексы сезонности можно определять на основе данных, полученных в результате применения метода аналитического выравнивания. Формула расчета индекса сезонности в рядах динамики с ярко выраженной тенденцией имеет следующий вид:

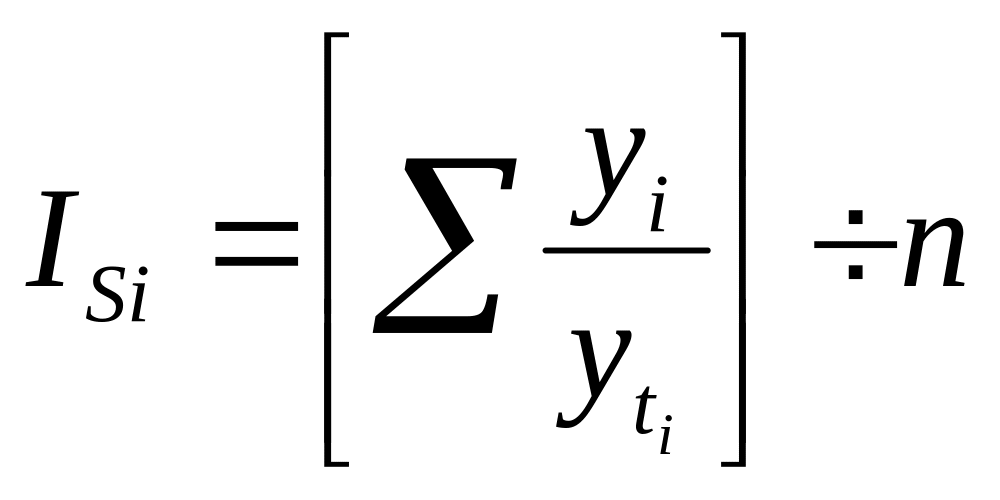, где у_i – исходные (эмпирические уровни ряда; – выравненные (теоретические) уровни ряда; n – число годовых периодов.