51 . Модели формирования портфеля ценных бумаг (задница,а не вопрос!!!!!!!)

1. Модель эффективного портфеля г. Марковица (1952 г.)

Подход Г. Марковица начинается с предположения, что инвестор в настоя­щий момент времени имеет конкретную сумму денег для инвести­рования. Эти деньги будут инвестированы на определенный про­межуток времени, который называется периодом владения. В кон­це периода владения инвестор продает ценные бумаги, которые были куплены в начале периода, после чего либо использует полученный доход на потребление, либо реинвестирует доход в раз­личные ценные бумаги (либо делает то и другое одновременно).

Г. Марковиц предположил, что распределение вероятностей значения доходности портфеля вокруг ее математического ожи­дания описывается симметричной нормальной кривой Гаусса. Введя понятие дисперсии (изменчивости) как меры риска, или неопределенности дохода, Г. Марковиц имел в виду, что распределение этой кривой вокруг среднего значения отража­ет изменчивость доходности портфеля — область возможных результатов и вероятностей отклонений фактической доходности портфеля от ожидаемой доходности.

Г. Марковиц использует термин «эффективный» для характери­стики портфеля, составленного из лучших по данной цене акций с минимальной изменчивостью доходности. Можно было бы гово­рить в данном случае об оптимизации. Подход объединяет два основных стереотипа поведения, понятных самому незрелому ин­вестору: кто не рискует, тот не выигрывает, но и не клади все яйца в одну корзину.

Не существует единственного эффективно­го портфеля, который был бы эффективнее всех остальных. Сред­ствами линейного программирования метод Марковица предла­гает меню эффективных портфелей. Как у всякого меню, у него две стороны: с одной стороны, желания, с другой — цена. Чем выше ожидаемый доход, тем больше риск. Но каждый из эф­фективных портфелей этого меню обеспечивает максимальный ожидаемый доход для заданного уровня риска или минимальный уровень риска для заданного ожидаемого дохода. Наиболее сложной процедурой в ходе реализации модели Марковица является накопление вычислений, необходимых для оценки того, как курсы разных акций или облигаций меняются по отношению к курсам других акций или облигаций.

Возможны два вида постановки задачи формирования оптимального портфеля. Первый тип задачи формирования оптимального портфеля Марковица можно определить как сформирование портфеля минимального риска из всех портфелей, имеющих эффективность не менее заданной. Минимизация вариации эффективности портфеля равносильна минимизации риска портфеля, поэтому задача Марковица может быть сформулирована следующим образом: необходимо найти доли X_i , минимизирующие риск портфеля:

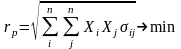, (31)

при условии, что обеспечивается заданное значение эффективно­сти портфеля Е_р, то есть 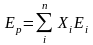и поскольку X_i - доли, то в сумме они должны составлять единицу, то есть выполняется бюджетный баланс: .

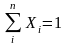Оптимальное решение этой задачи обозначим значком *. Если х_i^*  0, то это означает рекомендацию вложить долю х_i^* налично­го капитала в ценные бумаги i-го вида. Если же х_i^* < 0, то содер­жательно это означает провести операцию «short sale» («короткая продажа»). Если такие операции невозможны, значит необходимо ввести ограничения х_i^*  0.

Данный портфель минимального риска из всех портфелей задан­ной эффективности называется портфелем Марковица минималь­ного риска, а его риск r_р есть функция его заданной эф­фективности.

Второй тип задачи формирования оптимального портфеля – это формирование портфеля максимальной эффективности из всех портфелей, имеющих риск не более заданного. В данном случае необходимо найти x_i, максимизирующие ожидаемую эффективность пор­тфеля, то есть:

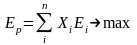, (32)

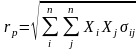при условии, что обеспечивается заданное значение риска порт­феля, то есть: и они должны составлять единицу, то есть .

Данную формализацию можно назвать портфелем Марковица мак­симальной эффективности.

Из описания теории Г. Марковица, можно сделать вывод, что она дает принципы построения эффективных портфелей и способы выбора из них наилучшего, или оптимального, портфеля.