17. Проверка параметрических гипотез

16. Проверка статистических гипотез о виде закона распределения при помощи критерия Пирсона.

Статистической называется гипотеза о виде неизвестного распределения или о параметрах известных распределений.

Для того, чтобы можно было воспользоваться критерием Пирсона и определить, насколько некоторая предлагаемая модель функции распределения (и, соответственно, плотности вероятности) соответствует экспериментальным данным, необходимо построить статистику ², вычисляемую по формуле:

П ри этом область значений вариационного ряда разбита на K интервалов. v_i – частота попадания значений выборки в i-ый интервал, p_i – теоретическое значение вероятности этого события, вычисляемое на основе проверяемой модели. Затем по заданному уровню значимости  определяется квантиль распределения ²(j-m-1) и сравнивается со значением G статистики критерия Пирсона, которая для принятия гипотезы о виде распределения должна не превосходить найденную квантиль.

17. Метод наименьших квадратов.

1) Общие сведения об мнк

Пусть переменная y является функцией x, y=f(x), где x - векторная (в общем случае) переменная размерности m. Имеется набор наблюдений , k=1,...,n. Функция f(x) считается неизвестной, и по имеющимся данным о ее значениях можно ее аппроксимировать какой-либо функцией заранее заданного вида (Θ - векторный параметр).

Метод наименьших квадратов предлагает определять наилучший набор параметров Θ для функций данного класса при помощи следующего критерия:

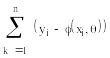->min (1)

Наиболее распространена линейная аппроксимация:

y = . (2)

Задача по нахождению векторного параметра b методом наименьших квадратов для независимых ,..., имеет единственное решение:

b = , (3)

где X=( | | ... | ) - матрица размера , где по столбцам стоят координаты векторов ,..., , а матрица А находится, как

A= (4)

2) Полиномиальная мнк-аппроксимация.

Если ищется аппроксимация функции одной переменной f(t) в виде многочлена

φ(t)= +...+ ,

по данным наблюдений f( ), f( ),...,f( ), то эту задачу также можно решать методом наименьших квадратов, считая x₁=( , ,..., ),..., x_n=( , ,..., ).

При m<=n вектор коэффициентов b будет найден единственным образом по формуле (3).

3) Стохастический вариант мнк - нормальная модель.

Пусть

у= , (5)

где y=( ,..., ), X=|| || - матрица порядка , ξ - случайный вектор, такой, что для любого k имеет распределение N(0, ). Иначе говоря, мы имеем набор наблюдений, значения которых "зашумлены" случайными нормально распределенными помехами с нулевым математическим ожиданием. МНК дает возможность найти оценки параметров b_k, k=1,...,m и неизвестной дисперсии (так называемые точечные оценки).

Формулы для их нахождения основываются на (2)-(4), точный их вид со своими обозначениями указан в расчетной части работы.

В предположении о нормальном распределении появляется возможность находить также и интервальные оценки неизвестных параметров по формуле:

^

^

P( <_i< )=1-

где С= , α - уровень значимости, выражения с крышками - точечные оценки, найденные из (3).

10