1. Виды вероятностной сходимости.

1. Сходимость по распределению (F).

2. Сходимость почти наверное (П.Н.)

3. Сходимость по вероятности (P)

4. Сходимость в среднем квадратическом (С.К.)

Взаимосвязь между видами сходимости:

2. Закон больших чисел

Смысл. Среднее значение случайной величины при достаточно большом количестве испытаний сколь угодно близко подходит к ее математическому ожиданию.

3. Центральная предельная теорема (ЦПТ)

Смысл. ЦПТ - свойство последовательности независимых случайных величин, позволяющее рассматривать их среднее арифметическое, как нормально распределенную СВ. Этим свойством обладают почти любые встречающиеся на практике последовательности случайных величин (начиная от исходов подбрасывания монеты). И поэтому оно очень важно.

4. Выборка и вариационный ряд.

Выборкой объема n называется случайный вектор X=(X₁, X₂,..., X_n)^Т, где СВ (случайные величины) X_i, i=1..n являются независимыми одинаково распределенными с функцией распределения F(x). Апостериорно выборка X является неслучайным вектором – набором n независимых реализаций одной и той же случайной величины.

Упорядоченный по возрастанию набор из неслучайных значений называется вариационным рядом выборки.

5. Выборочная функция распределения.

Эмпирической функцией распределения (или выборочной функцией распределения) называется ступенчатая функция построенная следующим образом:

,

где M(x)={число реализаций, значение которых не больше x}.

Выборочная функция распределения в каждой точке является оценкой F(x) - функции распределения.

Выборочная функция распределения всегда имеет ступенчатый вид.

6. Гистограмма

Гистограммой называется оценка функции плотности вероятности, получаемая по реализации выборки и состоящая из столбцов. Для ее построения вся область значений выборки разбивается на k одинаковых интервалов, k<<n. Далее подсчитывается количество значений выборки, принадлежащих каждому из интервалов m₁, m₂, … m₂. Затем подсчитываются соответствующие частоты v_i= m_i/n. Для выполнения условия нормировки для функции плотности

=1 – условие нормировки.

необходимо значения полученных частот разделить на длину интервалов, и далее строить над каждым интервалом столбец найденной высоты.

7. Выборочные моменты.

следующие два определения важны.

И это тоже полезное:

8. Распределения хи-квадрат и Стьюдента.

При работе с , , ..., - набором случайных величин, каждая из которых распределена по закону , часто возникает необходимость рассматривать распределение случайных величин, получающихся, как какая-либо комбинация всех этих величин. Основные такие распределения также, как и стандартное нормальное, посчитаны таблично для различных значений n.

1) Распределение хи-квадрат.

Распределение хи-квадрат с n степенями свободы, , - это распределение случайной величины

2) Распределение Стьюдента.

Распределение Стьюдента (или t-распределение) с n степенями свободы – это распределение случайной величины

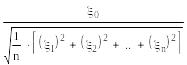
9. Точечные оценки и их свойства.

"статистика" - это какая-то функция (специальным образом построенная) от случайной величины. Т.е., тоже случайная величина.

Смысл. Точечная оценка - какое-то число (т.е., точка), получаемое по выборке. Этим числом оценивается какой-то неизвестный параметр.

Свойства оценок.

Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Ниже приведены важнейшие из них.

Пусть * - оценка неизвестного параметра  какого-то теоретического распределения. Допустим, по выборке объема n найдена оценка *₁. При использовании другой выборки, полученной по тому же распределению, будет определена оценка *₂. Повторяя опыт многократно с новыми выборками, получим набор значений *₁, *₂, …, *_n, которые будут различаться между собой. Таким образом, оценку * можно рассматривать, как случайную величину, а – как ее *₁, *₂, …, *_n возможные значения.

1) Несмещенность.

Несмещенной называется оценка, математическое ожидание которой равно оцениваемому параметру:

M(*)=

2) Состоятельность.

Состоятельной называется оценка, для которой вероятность

P{|*-|<}  1, при n  , для любого >0.

Т.е., при достаточно большом n вероятность того, что отклонение оценки от оцениваемого параметра не превысит любую, сколь угодно малую, величину стремится к единице. Иначе говоря, * стремится к  по вероятности.

3) Эффективность.

Эффективной называется статистическая оценка, имеющая (при заданном объеме выборки n) наименьшую возможную дисперсию