Равнопромежу­точности, равновеликости и равноугольности.

Ни одна географи­ческая карта с отображением сколько-нибудь значительной части земной поверхности (целого материка, океана, полушария или всей Земли) одновременно всеми тремя свойствами обладать не может, это и делает глобус незаменимым пособием при изучении географии в средней общеобразовательной школе. Он назван в перечне нагляд­ных пособий по географии средней школы.

свойство равнопромежуточн о с т и: Масштаб расстояний на глобусе одинаков во всех его частях. Это значит, что если масштаб глобуса 1:50 млн., то и радиус Земли, и ее окружность, и любое земное расстояние на поверхности уменьшено в 50 млн. раз. Благодаря свойству равнопромежуточности меридианы, имеющие на Земле равную протяженность, и на глобусе равны по длине; параллели же уменьшаются с удалением от экватора (и на Земле и на глобусе).

свойством равновели­ко с т и: При равенстве масштабов глобуса во всех его частях и по всем направлениям одинаков у него повсеместно и масштаб площадей. Его следствием является то, что равные по площади гео­графические объекты и на поверхности глобуса занимают одинако­вые по величине участки. То же можно сказать о сферических тра­пециях, образованных пересечением соседних меридианов и парал­лелей: расположенные на одной широте сферические трапеции равны по площади как на самом земном эллипсоиде, так и на глобусе.

свойство равноуголь­но с т и: означает, что величина горизонтальных углов между любыми двумя направлениями на земном эллипсоиде не изменяется при изображении этих направлений на глобусе. В частности, прямые сферические углы при пересечении меридианов и параллелей оста­ются и на глобусе прямыми.

Кратчай­ший путь между двумя точками на поверхности шара представляет собой дугу большого круга, т. е. линию, образованную пересечением шара плоскостью, проходящей через его центр и две данные точки - ОРТОДРОМИЯ. Например, чтобы установить ее направление между Москвой и Гаваной, достаточно натянуть на поверхности глобуса нитку, проходящую через обе эти столицы Положение нитки и покажет трассу вдоль дуги боль­шого круга, называемую в картографии ортодромией (греч.— «прямой путь»).

Несмотря на обилие иных картографических произведений, глобус до сих пор остается незаменимым, ибо обладает рядом свойств, присущих только ему.

1. Глобус практически правильно передает обобщенную форму Земли.

2. Глобус правильно передает соотношение диаметра Земли и рельефа ее поверхности.

3. Глобус правильно передает размеры (длины линий и пло­щади), формы и взаимное расположение объектов.

4. С помощью глобуса можно наглядно представить враще­ние Земли вокруг своей оси, а также наклон земной оси к плос­кости орбиты (66°33')-

Задачи, решаемые при помощи глобуса.

1. Определение географических координат объектов.

2. Измерение длин линий и площадей объектов.

3. Построение линий кратчайших расстояний между объектами.

4. Сопоставление географической сетки на глобусе с картографическими сетками для установления вида и величины ис­кажений на картах.

5. Ориентирование глобуса.

ИЗОБРАЖЕНИЕ ЗЕМНОГО ЭЛЛИПСОИДА НА ПЛОСКОСТИ. ПОНЯТИЕ ОБ ЭЛЛИПСЕ ИСКАЖЕНИЙ.ГЛАВНЫЙ И ЧАСТНЫЙ МАСШТАБЫ. СПОСОБЫ ОПРЕДЕЛЕНИЯ ИСКАЖЕНИЙ

Рассматривая вопрос о переходе от земной поверхности к ее изображению на плоскости, можно условно выделить три этапа:

- проектирование точек физической поверхности Земли на поверхность эллипсоида;

- уменьшение эллипсоида в требуемом масштабе (преобразова­ние эллипсоида в глобус);

- "разворачивание" глобуса в плоскость.

Степень уменьшения эллипсоида зависит от масштаба карты, который будем именовать главным масштабом. При создании кар­ты возможно сохранение величины исходного масштаба вдоль неко­торых направлений. Этот неизмененный масштаб глобуса, условно принятый за основу при построении карты, называют главным масштабом.

Способ перехода от глобуса к плоскости связан с выбранной для этой цели карто­графической проекцией. При этом линии параллелей и меридиа­нов образуют картографическую сетку, а их пересечения - узлы картографической сетки. Перечисленные элементы в совокупно­сти составляют математическую основу карт.

Поверхность Земли или ее модели не может быть развернута на плоскости без разрывов или перекрытий. Это приводит к тому, что изображение в одних случаях приходится растягивать, в дру­гих - сжимать, что нарушает геометрические свойства изображае­мой поверхности.

Такие нарушения в картографии называются искажениями.

Ис­кажения могут быть присущи длинам линий, площадям объектов, углам между направлениями, а следовательно, формам объектов.

Искажения длин линий выражаются в том, что линии, одинаковые на поверхности эллипсоида, на карте отображаются отрезками разной величины. Это обусловлено тем, что масштаб длин на карте меняется при перемене места, а также при смене направления в данной точке. Чем длиннее отрезок на карте, тем больше в его пределах будет различаться масштаб длин. Поэто­му для строгого определения масштаба карты воспользуемся по­нятием отрезка с минимально воображаемой длиной.

Масштабом длин будем называть отношение бесконечно ма­лого отрезка на карте к его горизонтальной проекции на поверх­ности эллипсоида или шара.

Искажение площадей состоит в том, что равновеликие объекты отображаются в различных частях карты фигурами разной площади. Соответственно масштаб площадей также различен в раз­ных частях карты (кроме специальных равновеликих проекций). По аналогии масштабом площадей называется отношение величин бесконечно малой площади на карте к соответствующей величине бесконечно малой площади на поверхности эллипсоида или шара.

Искажение углов заключается в том, что углы между ка­кими-либо направлениями на карте не равны горизонтальным углам между теми же направлениями на поверхности земного эллипсоида.

По этой причине, а также из-за искажений длин нарушается форма объектов. Искажение форм -отклонение от подобия форм объектов на карте и форм соответствующих объектов на эллипсоиде или шаре называется.

Все виды искажений на картах связаны между собой: при изменении длин нарушаются площади объектов; зачастую определенному искажению углов на карте соответствует одно и то же искажение форм. Особая связь существует между искаже­нием площадей и искажением углов: увеличение одного из них влечет уменьшение другого.

Анализируя любую карту с целью выявления присущих ей искажений, сначала устанавливают их вид, а затем характер распределения и величины.

Наличие искажений легко установить, сравнивая картографи­ческую сетку с неискаженной географической сеткой на глобусе. При этом, однако, следует помнить, что если какое-либо из пе­речисленных свойств на карте не нарушается, то это еще не га­рантирует отсутствие на ней соответствующего вида искажений. К тому же на мировых картах и картах полушарий искажения легко установить при визуальном просмотре, на картах матери­ков и океанов выявить искажения таким образом труднее, а на картах Республики Беларусь и ее регионов это уже практически невозможно.

При анализе характера распределения искажений в первую очередь необходимо установить места, где искажения отсутству­ют, и участки карты с максимальными величинами искажений.

Места, где на карте искажений нет, называют точками или линиями нулевых искажений. Эти точки или линии являются общими для глобуса и полученной на его основе карты. На карте может быть одна или две точки либо одна или две линии нуле­вых искажений данного вида. Незначительная часть картогра­фических проекций вместо точек нулевых искажений имеет точ­ки минимальных искажений. При удалении от всех перечислен­ных точек и линий величины искажений на картах растут, одна­ко скорость возрастания зависит от направления. Поэтому, если на карте получается одна точка нулевых искажений, ее старают­ся поместить в центре карты. Так же поступают и в отношении одной линии нулевых искажений.

Однако при любом расположении нулевых и минимальных искажений величина максимальных искажений на карте зави­сит от размеров изображаемой территории. Для расчета количе­ственных характеристик искажений пользуются показателями масштабов.

Главный масштаб сохраняется только в точках и линиях, где нет искажений.

Масштабы во всех других точках карты, отлича­ющиеся от главного, называются частными. Чем сильнее разли­чаются масштабы, тем больше искажений, поэтому показатели искажений рассчитываются как отношение частного масштаба в конкретной точке карты по определенному направлению к глав­ному масштабу карты и выражаются в долях единицы, посколь­ку при их равенстве отношение равно 1.

Главный масштаб, как правило, подписывают на карте, а ча­стный подлежит определению. Для его расчета необходимо произ­вести ряд измерений по карте и применить формулы, используе­мые в математической картографии.

Анализируя искаженность карты, можно не только установить наличие или отсутствие картографического искажения того или иного вида, но и измерить величины этих искажений. Такую зада­чу решают, вычислив показатели искажений.

Показатель искажения длин  имеет особые обозначения, если он направлен по меридиану (m), по параллели (n). Самый большой показатель искажения длин у данной точки обозначают латинской буквой а, а наименьший — буквой b. Сами же взаимно перпенди­кулярные направления, по которым действуют наибольший и наи­меньший показатели искажения длин, называют главными направлениями.

За показатель искажения углов между линиями картографичес­кой сетки принимают величину отклонения их от 90° и обозначают его греческой буквой  (эпсилон).

 = — 90°,

где  (тэта) — измеренный на карте угол между ме­ридианом и параллелью.

В точке, где угол пересечения меридиана и параллели оста­ется на карте прямым, углы между другими направлениями могут быть измененными на карте, поскольку в каждой данной точке величина искажения углов может изменяться с переменой направ­ления.

За общий показатель искажения углов  (омега) принима­ют наибольшее искажение угла в данной точке, равное разности его величины на карте и на поверхности земного эллипсоида (или шара). При известных показателях a и b величину  узнают по формуле:

Sin  = a + b

2 а — b

Показатель искажения площадей (р) вычисляют как произве­дение наибольшего и наименьшего показателей искажения длин в данном месте карты:

р = а b

Главные направления в данной точке карты могут совпадать с ли­ниями картографической сетки, но могут с ними не совпадать. Тог­да показатели а и b по известным m и n вычисляют по соответствующим фор­мулам.

Показатель искажения форм (k) зависит от различия наибольше­го (а) и наименьшего (b) показателей искажения длин в данном месте карты и выражается формулой:

K = а/b

Виды искажений и их величину в конкретном месте карты можно наглядно отобразить с помощью эллипсов искажений.

Эллипса­ми искажений называют изображенные на карте геометриче­ские фигуры (эллипсы или круги), формы и размеры которых соот­ветствуют видам и величине искажений, имеющихся в центральной точке фигуры.

По одному из направлений растяжение будет максимальным (большая ось эллипса), по перпендикулярному ему - минималь­ным (малая ось). По всем остальным направлениям масштаб бу­дет иметь промежуточное значение.

Направления в конкретной точке на карте, по одному из кото­рых масштаб длин имеет наибольшее, а по другому — наименьшее значение, называются главными направлениями. Если необхо­димо определить направление и степень растяжения или сжатия географического объекта в конкретном месте на карте, надо в данной точке построить эллипс искажений.

Для этого рассчитывают дополнительный параметр: угол меж­ду осью эллипса и меридианом данной точки  :

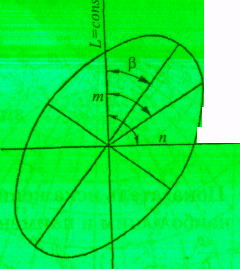
Величина искажений зависит не только от территориального охвата карты, но и от способа переноса изображения с глобуса на плоскость, т.е. от картографической проекции.

Характер распределения искажений на карте можно устано­вить, не прибегая к вычислениям соответствующих показателей. Для этих целей существуют макеты изокол. Это уменьшенное изображение карт с нанесенными на них линиями, соединяющи­ми точки с одинаковыми показателями искажений . Интерполируя между изоколами, можно определить величину ис­кажений в любой точке на карте. Для каждого вида проекции име­ются характерные только ей изоколы длин, площадей, углов.

Можно также использовать таблицы искажений, в которых приведены величины

а, b , р и k для узловых точек картографи­ческой сетки. Величина того или иного показателя для цент­ральной точки объекта может быть получена интерполировани­ем между узловыми точками.