Диаграмма растяжения

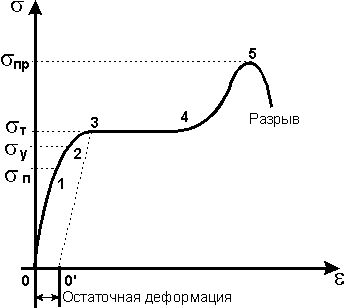И спользуя формулу (2.13), по экспериментальным значениям относительного удлиненияe можно вычислить соответствующие им значения нормального напряжения s, возникающего в деформированном теле, и построить график зависимости s от e. Этот график называют диаграммой растяжения. Подобный график для металлического образца изображен на рис. 22. На участке 0-1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения s_п, при котором еще выполняется закон Гука, называют пределом пропорциональности.При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1-2), хотя упругие свойства тела еще сохраняются. Максимальное значение s_у нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2-3) приводит к тому, что деформация становится остаточной.Затем образец начинает удлиняться практически при постоянном напряжении (участок 3-4 графика). Это явление называют текучестью материала. Нормальное напряжение s_т, при котором остаточная деформация достигает заданного значения, называют пределом текучести.При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4-5 графика). Максимальное значение нормального напряжения s_пр, при превышении которого происходит разрыв образца, называют пределом прочности.

Энергия упруго деформированного тела

Подставив в формулу (2.13) значения s и e из формул (2.11) и (2.12), получим

f_уп/S=E|DL|/L₀.

откуда следует, что сила упругости f_уп, возникающая при деформации тела, определяется по формуле

f_уп=ES|DL|/L₀.    (2.14)

Определим работу A_деф, совершаемую при деформации тела, и потенциальную энергию W упруго деформированного тела. Согласно закону сохранения энергии,

W=A_деф.    (2.15)

Как видно из формулы (2.14), модуль силы упругости может изменяться. Он возрастает пропорционально деформации тела. Поэтому для подсчета работы деформации необходимо брать среднее значение силы упругости <f_уп>, равное половине от ее максимального значения:

<f_уп>= ES|DL|/2L₀.    (2.16)

Тогда определяемая по формуле A_деф=<f_уп>|DL| работа деформации

A_деф= ES|DL|²/2L₀.

Подставив это выражение в формулу (2.15), найдем значение потенциальной энергии упруго деформированного тела:

W= ES|DL|²/2L₀.    (2.17)

Для упруго деформированной пружины ES/L₀=k - жесткость пружины; х - удлинение пружины. Поэтому формула (2.17) может быть записана в виде

W=kx²/2.    (2.18)Формула (2.18) определяет потенциальную энергию упруго деформированной пружины.

Ответ 13