Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Омский государственный технический университет»

А.Л. Ануфриенко, В.С. Калекин

Процессы и аппараты химической технологии.

Массообменные процессы

Учебное пособие для практических занятий

и самостоятельной работы студентов

Омск-2007

УДК 66+532+536.24 (075)

ББК 35+22.253+35.112 я73

А 73

Рецензенты:

А.С. Ненишев, д-р техн. наук, проф., заведующий кафедрой «Теплотехника и тепловые двигатели», СибАДИ

М. Д. Смоликов, канд. хим. наук, ст. науч. сотрудник, ИППУ СО РАН

Ануфриенко А.Л., Калекин В.С.

А 73 Процессы и аппараты химической технологии. Массообменные процессы: Учебное пособие для практических занятий и самостоятельной работы студентов. Омск: Изд-во ОмГТУ, 2007. 105 с.

В учебном пособии представлены примеры и задачи по разделу дисциплины «Процессы и аппараты химической технологии»: массообменные процессы. По каждой теме кратко приводятся основные формулы и определения.

В приложении представлены справочные данные в виде таблиц, диаграмм и номограмм, используемых при расчётах химической аппаратуры.

Для студентов специальности 240401 «Химическая технология органических веществ» и 240801 «Машины и аппараты химических производств ».

Печатается по решению редакционно-издательского совета Омского государственного технического университета.

УДК 66+532+536.24 (075)

ББК 35+22.253+35.112 я73

© А.Л. Ануфриенко,

В.С. Калекин, 2007

© Омский государственный

технический университет, 2007

Содержание

1. ОСНОВЫ МАССОПЕРЕДАЧИ 5

2. АБСОРБЦИЯ 18

3. ПЕРЕГОНКА И РЕКТИФИКАЦИЯ 35

4. СУШКА 53

5. ВЫПАРИВАНИЕ, КРИСТАЛЛИЗАЦИЯ 67

Библиографический список 78

Приложение 1 79

Равновесные составы жидкости 79

и пара для некоторых бинарных систем 79

при П_АБС=760 мм рт. ст. 79

Приложение 2 80

Значения коэффициента Генри Е для водных растворов некоторых газов 80

Приложение 3 81

Коэффициенты диффузии газов и паров в воздухе 81

Приложение 4 81

Коэффициенты диффузии некоторых газов в воде при 20 ^оС ^* 81

Приложение 5 82

Характеристики скрубберных насадок из колец и кускового материала 82

Приложение 6 83

Динамические коэффициенты вязкости воды 83

Приложение 7 84

Свойства насыщенного водяного пара в зависимости от давления 84

Приложение 8 86

Мольная теплоемкость газов, кДж/(кгК) (при р_абс=1атм)^* 86

Приложение 9 87

Давление насыщенного водяного пара 87

при температурах от - 20 до 100 °С 87

Приложение 10 88

Свойства насыщенного водяного пара в зависимости от температуры 88

Приложение 11 90

Концентрации [в % (масс.)] некоторых водных растворов, кипящих под атмосферным давлением 90

Приложение 12 91

Физические свойства воды (на линии насыщения) 91

Приложение 13 92

Кривые равновесия (с азеотропной точкой) при П = 760 мм рт. ст. 92

Приложение 14 92

Кривые равновесия при П = 760 мм рт. ст. 92

Приложение 15 94

Номограмма для определения давления насыщенного пара и температуры кипения некоторых жидкостей 94

Приложение 16 96

Давление насыщенного пара органических жидкостей, не смешивающихся с водой, в зависимости от температуры 96

Приложение 17 97

Номограмма для определения теплоёмкостей жидкостей 97

Приложение 18 99

Зависимость давления насыщенного пара гексана от температуры 99

Приложение 19 100

Повышение температуры кипения водных растворов при атмосферном давлении в зависимости от концентрации. 100

Приложение 20 101

Диаграмма линейности для определения температуры кипения (по воде) 101

Приложение 21 102

Диаграмма линейности для определения температуры кипения 102

(по гексану) 102

1. Основы массопередачи

Процессами массообмена называют такие процессы, в которых основную роль играет перенос вещества из одной фазы в другую. Движущая сила этих процессов разность химических потенциалов. Движущая сила массообмена характеризует степень отклонения системы от состояния динамического равновесия. В пределах данной фазы вещество переносится от точки с большей к точке с меньшей концентрацией. Поэтому движущую силу выражают через разность концентраций, что значительно упрощает расчеты массообменных процессов.

1. Способы выражения состава фаз в массообменных процессах.

Концентрацией называется величина, выражающая содержание какого – либо компонента в смеси (в фазе, в системе из нескольких фаз, в том или ином сечении технологического аппарата, в части аппарата или в аппарате в целом). Концентрация компонента задаётся отношением его количества к количеству какого - либо другого компонента смеси, нескольких или всех её компонентов.

Совокупность всех концентраций смеси даёт её состав.

Поскольку концентрации участвующих в массообменных процессах фаз могут иметь различную размерность (кг/кг, кмоль/м³ и т.п.), то целесообразно рассмотреть способы выражения состава этих фаз. Обычно состав фаз выражают в массовых или молярных долях, относительных или объёмных концентрациях.

Абсолютные и относительные концентрации различаются базой расчёта: абсолютные (за базу принята сумма всех компонентов смеси), относительные (база – какой – то один компонент).

Составы фаз двухкомпонентных систем

Наиболее часто применяются следующие способы выраже­ния концентрации компонента А в жидкой смеси компонен­тов А и В.

Мольная доля:

(1.1)

Массовая доля:

(1.2)

Относительная мольная концентрация:

(1.3)

Относительная массовая концентрация:

(1.4)

Чтобы выразить состав в процентах, результат вычисления по формулам (1.1) – (1.4) нужно умножить на 100.

Выражение объёмного состава фаз (с_А, с_В, ...) в кг/м³ связано с массовыми долями этих компонентов в смеси следующим образом:

х_i = c_i / ρ

Объемная мольная концентрация:

(1.5)

Объемная массовая концентрация:

(1.6)

Формулы для пересчета концен­траций жидкой фазы приведены в табл. 1.1.

Таблица 1.1

Выражение концентра­ции	х		X		Сх
х	1	или			или	или
		1
X			1
				1
Сх					1
						1
МА, МВ и МСМ – мольные массы компонентов А и В и смеси, кг/кмоль; МСМ = МАх + МВ(1 - х); ρ – плотность смеси, кг/м3; Для смеси идеальных газов:

Для газовой (паровой) фазы справедливы те же соотношения, но с заменой обозначений х на y, X на Y, С_Х на С_Y.

Концентрация компонента в газовой фазе может быть выражена также через его парциальное давление. Мольная (объёмная) доля у любого компонента смеси идеальных газов равняется:

,

где р – парциальное давление компонента газовой смеси;

П – общее давление смеси газов или паров.

2. Законы межфазного равновесия для идеальных смесей.

Смесь двух взаимно растворимых в любых отношениях жид­костей.

а) Закон Рауля — для систем жидкость — пар при температу­рах ниже критических:

р*_Н.К.=Р_Н.К.·х _Н.К. и р*_В.К = Р_В.К (1 - х_Н.К.). (1.7)

где р*_Н.К., р*_В..К – парциальное давление низкокипящего и высококипящего компонента в паровой фазе над жидкостью в условиях равновесия;

Р_Н.К. , Р_В.К. – давление насыщенного пара чистого низкокипящего и высококипящего компонента при данной температуре;

х_Н.К. , х_В.К – мольная доля низкокипящего и высококипящего компонента в жидкой фазе,

б) Общее давление смеси идеальных газов определяется законом Дальтона:

П = р_А+р_В+р_С+....

или

р_А = П· y_А

р_В = П· y_В и т. д. (1.8)

где П – общее давление смеси газов или паров;

р_А, р_В , ... – парциальные давления компонентов А, В, ...;

y_А, y_В – мольные доли компонентов А, В . . . в газовой фазе.

в) Уравнение Рауля—Дальтона (уравнение равновесия пара и жидкости для идеального раствора):

у*(х) =p*_Н.К./П = Р_Н.К. ·х_Н.К./[Р_Н.К.х_Н.К.+ Р_В.К.(1 – х_Н.К.)] = Р_Н.К. ·х_Н.К./П (1.9)

где у^*_Н.К. – мольная доля низкокипящего компонента в паре, равновесном с жид­костью состава х_Н.К..

На рис. 1.1. показана связь между долей летучего компо­нента в жидкости "х" и равновесной его долей в паре у*(х) – пунктирная кривая. Гра­фик в координатах у* - х всегда имеет вид квадрата с единичны­ми сторонами (х = 1 и у* = 1), в качестве вспомогательной линии на нем изображается диагональ, что делает кривую равновесного состава более наглядной.

Выразив уравнение 1.9. через коэффициент относительной летучести получим:

, (1.9а)

где – коэффициент относительной летучести;

р_Н.К. – давление насыщенного пара более летучего (низкокипящего) компонента;

р_В.К. – давление насыщенного пара менее летучего (высококипящего) компонента при той же температуре.

Сведения о равновесных составах жидкости и пара, опре­деляемые обычно опытным путем, имеются в справочниках. Для некоторых бинарных смесей данные о разновесных составах жидкости и пара при П = const имеются в прил. 1, 13 и 14.

г) Закон Генри — для систем жидкость — газ при температурах газа выше критических:

р* = Ех (1.10)

где р* – парциальное давление компонента в газовой фазе над жидкостью в условиях равновесия;

х – мольная доля компонента в жидкой фазе;

Е – коэффициент Генри, изменяющийся с температурой и зависящий от природы газа и растворителя, размерность его та же, что и р*.

Значения Е для водных растворов некоторых газов даны в прил. 2.:

Так как р = у·П [формула (1.8.)], то уравнение (1.10) приво­дится к виду:

у* = m ·х (1.11)

где у* – мольная доля компонента в газовой фазе, равновесной с жидкой;

безразмерная величина, постоянная при t = const и П = const.

3. Нарушение фазового равновесия в массообменных процессах.

Во всех массообменных процессах общим является переход вещества (или нескольких веществ) из одной фазы в другую в направлении достижения равновесия, его называют массопередачей.

В отличие от теплопередачи, которая происходит обычно через стенку, массопередача осуществляется при непосредственном соприкосновении фаз (за исключением мембранных процессов).

Граница соприкосновения – поверхность контакта фаз может быть подвижной (система газ – жидкость, пар – жидкость, жидкость – жидкость) или неподвижной (газ – твёрдое тело, пар – твёрдое тело, жидкость – твёрдое тело).

Перенос вещества внутри фазы – из фазы к границе раздела фаз или наоборот – от границы раздела в фазу – называют массоотдачей.

Массообменные процессы протекают лишь при нарушении фазового равновесия. Только при этом условии распределяемое вещество переходит из одной фазы в другую. При этом различают два вида переноса вещества – молекулярный и конвективный.

В неподвижной среде распределяемое вещество переходит из внутренних слоёв данной (первой) фазы к поверхности раздела фаз и, пройдя её, распределяется по всему объёму другой фазы, находящейся в контакте с первой. Такой переход массы вещества из одной фазы в другую называют молекулярной диффузией. Она является следствием теплового движения молекул (ионов, атомов), которому оказывают сопротивление силы внутреннего трения.

Молекулярная диффузия описывается первым законом Фика:

,

где D – коэффициент молекулярной диффузии;

F – поверхность, нормальная к направлению диффузии;

– градиент концентраций вещества на единицу длины пути n диффундирующего вещества;

знак минус связан с уменьшением градиента концентраций по длине пути диффузии.

Под диффузией (массопроводностью) понимают перенос вещества без перемещения частиц рабочего тела (газа, жидкости, твёрдого).

Коэффициент молекулярной диффузии D (м²/с) показывает, какое количество вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

а) Коэффициент диффузии газа А в газе В (или газа В в газе А) может быть вычислен по формуле:

, (1.12)

где T – температура, °К;

P – давление (абсолютное), Па;

M_A и М_В – молекулярные массы газов А и В;

υ_A и υ_B – молекулярные объемы газов А и В, см³/моль, определяемые, как сумма атомных объемов элементов, входящих в состав газа. Молекулярные и атомные объемы некоторых веществ приведены в табл. 1.2.

Структурные постоянные (при расчёте мольного объёма соединения величину соответствующей структурной постоянной надо прибавить к сумме атомных объёмов):

Бензольное кольцо —15

Нафталиновое кольцо —30

Антраценовое кольцо —47,5.

Таблица 1.2.

Атомный объем, см3/атом
В	27,0	О в альдегидах и кетонах	7,4
С	14,8	О в сложных эфирах	9,1
С1	24,6	О в простых эфирах	9,9
Н	3,7	О в высших простых и сложных эфирах	11,0
N в первичных аминах	10,5	О в кислотах	12,0
N во вторичных аминах	12,0	О в соединениях с S, Р, N	8,3
N с двумя насыщенными связями	15,6	S	25,6
О с двумя насыщенными связями	7,4	I	37,0
Молекулярный объем, см3/моль
Н2	14,1	N2O	36,4
О2	25,6	NH3	25,8
N2	31,2	H2O	18,9
Воздух	29,9	H2S	32,9
СО	30,7	COS	51,5
СО2	34,0	Cl2	48,4
SO2	44,8	Br2	53,2
NO	23,6	I2	71,5

Как следует из формулы (1.12), если известно значение коэф­фициента диффузии D₁ при температуре Т₁ и давлении Р₁, то зна­чение его D₂ при температуре Т₂ и давлении Р₂ можно найти из уравнения:

(1.13)

Значения коэффициентов диффузии в воздухе для некоторых газов и паров приведены в прил. 3.

б) Коэффициент диффузии в жидкости D_Ж при 20° С можно вычислить по приближенной формуле:

, (1.14)

где μ – вязкость жидкости, мПа·с;

υ_A и υ_B – молекулярные объёмы растворённого вещества и растворителя;

М_А и М_В – молекулярные массы растворённого вещества и растворителя;

А и В – коэффициенты, зависящие от свойств растворен­ного вещества и растворителя.

Значения коэффициента А для некоторых веществ, растворен­ных в воде:		Коэффициент В равен:
для газов	1,0	для воды	4,7
» этилового спирта	1,24	» этилового спирта	2,0
» метилового спирта	1,19	» метилового спирта	2,0
» уксусной кислоты	1,27	» ацетона	1,15
		» неассоциированных жидкостей	1,0

Коэффициент диффузии газа в жидкости D_t (при температуре t) связан с коэффициентом диффузии D₂₀ следующей приближенной зависимостью:

, (1.15)

в которой температурный коэффициент b может быть определен по эмпирической формуле:

(1.16)

где μ – вязкость жидкости при 20° С, мПа·с;

ρ – плотность жидкости, кг/м³.

Значения коэффициентов диффузии некоторых газов в воде приведены в прил. 4.

в) Более точная формула для определения коэффициента диф­фузии в разбавленных растворах:

где М – молекулярная масса растворителя;

υ – молекулярный объем диффундирующего вещества;

Т – температура, °К;

μ – вязкость растворителя, мПа·с;

β – параметр, учитывающий ассоциацию молекул раствори­теля и равный:

для воды	2,6
» метилового спирта	1,9
» этилового спирта	1,5
» бензола, эфира, гептана	1.

Конвективный перенос (конвективная диффузия) характеризуется перемещением вещества движущимися частицами потока в условиях турбулентного движения фаз. Конвективный перенос вещества под действием турбулентных пульсаций иногда называют турбулентной диффузией.

Под конвективным массопереносом понимают процесс переноса вещества при движении жидкости или газа. Этот процесс происхо­дит как бы механически - макрообъемными частицами жидкостного или газового потока.

В соответствии с двумя возможными способами выражения движущей силы процесса массопередачи — по газовой фазе (Δу = у* - у) или по жидкой фазе (Δх = х - х*) — ypaвнение массопередачи, аналогичное уравнению теплопередачи, быть написано в двух видах:

(1.17)

или

. (1.18)

где М – расход компонента, переходящего из одной фазы в другую, кмоль/с;

F – площадь поверхности массопередачи, м²;

К_y – коэффициент массопередачи, отнесенный к движущей силе Δу, выраженной через мольные доли компонента в газовой фазе, кмоль/(м²·с);

К_x – коэффициент массопередачи, отнесенный к движущей силе Δх, выраженной через мольные доли компонента в жидкой фазе, кмоль/(м²·с);

Δy_СР и Δх_СР – соответствующие средние для всего процесса движущие силы (уравнения 2.7, 2.8, 2.9).

Вместо мольных расходов и концентраций могут быть массовые, а вместо Δy_СР могут быть ΔY_СР, ΔС_yср и Δр_СР; соответственно, вместо Δх_СР могут быть ΔХ_СР или ΔС_хср .

г) При определенных допущениях (отсутствие диффузионного сопротивления при переходе компонента через поверхность раздела фаз, существование равновесия на этой поверхности, линейность уравнения равновесия у* = mх или у* = тх + b) получаются следующие зависимости между коэффициентами массопередачи К_y и К_х и фазовыми коэффициентами массоотдачи β_у и β_х:

; (1.19)

, (1.20)

где т – тангенс угла наклона линии равновесия. Коэффициенты массоотдачи и массопередачи выражены в кмоль/(м²·с).

Знаменатели последних уравнений представляют собою общее диффузионное сопротивление, равное сумме диффузионных сопротивлений газовой и жидкой фаз.

Когда основное диффузионное сопротивление сосредоточено в газовой фазе, т. е. при , .

Когда основное диффузионное сопротивление сосредоточено в жидкой фазе, т.е. при , .

Из уравнений (1.19) и (1.20) следует, что

. (1.21)

4. Основные диффузионные критерии подобия установившихся процессов массоотдачи.

Диффузионный критерии Нуссельта:

.

Диффузионный критерий Пекле:

.

Диффузионный критерий Прандтля:

.

Здесь β – коэффициент массоотдачи, м/с;

l – характерный линейный размер, м;

D – коэффициент молекулярной диффузии, м²/c;

ω – скорость газа или жидкости, м/с;

ν – кинематический коэффи­циент вязкости, м²/с.

Коэффициент массоотдачи β (м/с) показывает, какое количество ве­щества переходит от единицы поверхности раздела фаз в ядро потока (или наоборот) в единицу времени при движущей силе, равной единице.

Примеры.

1. Вычислить коэффициент диффузии сероводорода в воде при 40 ºС.

Решение: Сначала вычислим коэффициент диффузии при 20 ºС по формуле (1.14):

Для воды:

В = 4,7; μ = 1 мПа·с; υ_А = 2·3,7+7,4=14,8; М_А = 18

Для сероводорода:

А = 1; υ_В = 2·3,7+ 25,6 = 33,0; М_В = 34

Подставляем значения в формулу (1.14):

м²/с

Вычисляем температурный коэффициент b формулы (1.16):

Искомый коэффициент диффузии по формуле (1.15) равняется:

D₄₀ = 1,93·10^-9[l +0,02 (40-20°)]=2,7·10^-9 м²/с

Здесь 0,656 мПа·с — динамический коэффициент вязкости воды при 40 °C.

2. В ректификационной колонне непрерывного действия происходит разделение бинарной смеси бензол – толуол при атмосферном давлении.

Определить коэффициент диффузии в жидкости и в паровой фазе при t= 89 °С.

Решение:

Коэффициенты диффузии в жидкости D_x20 при 20 °С:

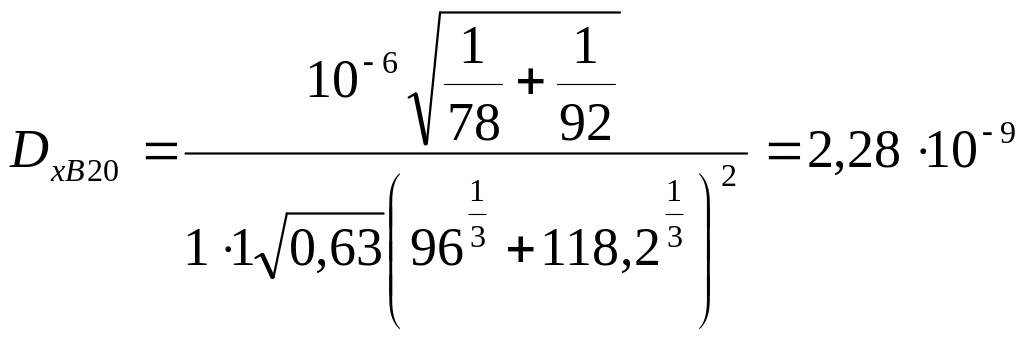м²/с,

где А=1, В=1 – коэффициенты, зависящие от свойств растворенного вещества и растворителя;

υ_б, υ_Т – мольные объемы компонентов в жидком состоянии при температуре кипения, см³/моль;

μ_x – вязкость жидкости при 20 °С, мПа·с. Вязкость толуола μ_x = 0,6 мПа

Температурный коэффициент b определяют по формуле (1.16):

Здесь μ_х и ρ_х принимаются при температуре 20 °С.

Коэффициент диффузии в жидкости при средней температуре t (в °С) равен:

D_х = D_{х 20}[1+ b(t - 20)] = 2,28·10^-9[l + 0,017 (89 — 20)] = 4,6·10^-9 м²/с.

Коэффициент диффузии в паровой фазе может быть вычислен по уравнению (1.12):

м²/с

где Т – средняя температура в соответствующей части колон­ны, К;

Р – абсолютное давление в колонне, Па.

3. Жидкая смесь содержит 58,8% (мол.) толуола и 41,2% (мол.) четыреххлористого углерода (ч.х.у.). Определить относительную массовую концентрацию толуола и его объемную массовую концентрацию С_х (в кг/м³).

Решение: Относительная массовая концентрация толуола:

где М_ТОЛ – мольная масса толуола (92 кг/кмоль);

М_Ч.Х.У – то же четыреххлористого углерода (154 кг/кмоль);

х – мольная доля толуола.

Получим:

Чтобы рассчитать объемную массовую концентрацию толуола , необходимо знать плотность смеси ρ_СМ. Для расчета плотности предварительно найдем массовую долю толуола.

Далее находим: плотность толуола ρ_ТОЛ = 870 кг/м³, плотность четыреххлористого углерода ρ_Ч.Х.У= 1630 кг/м³.

Считая, что изменение объема при смешении не происходит, т. е. объем смеси равен сумме объемов компонентов, находим объем 1 кг смеси:

м³ ,

откуда плотность смеси:

кг/м³ .

Можно рассчитать ρ_СМ и так:

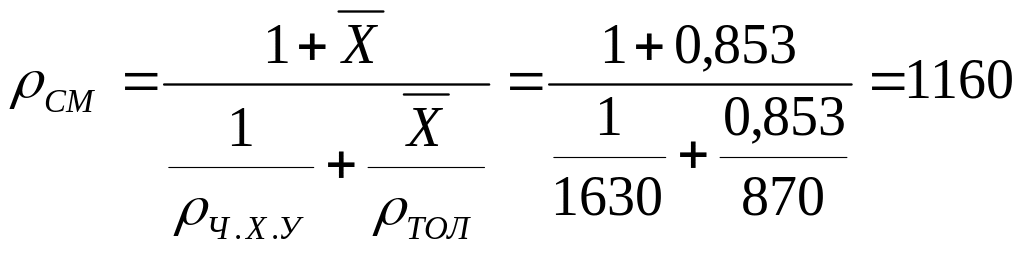кг/м³ .

Объемная массовая концентрация толуола:

кг/м³.

4. Вычислить состав равновесной паровой фазы при 50⁰С для жидкости, состоящей из смеси гексана и воды, предполагая их полную взаимную нерастворимость.

Решение: Давление насыщенного пара гексана при 50⁰С равняется 400 мм рт. ст. (прил. 16). Давление насыщенного пара воды при 50⁰С 92,5 мм рт. ст. (прил. 16). Каждое из веществ будет развивать давление пара вне зависимости от присутствия другого.

Общее давление смеси паров:

П = р_В+р_Г = Р_В + Р_Г = 400 + 92,5 =492,5 мм рт.ст

Долю гексана в паровой фазе найдём по уравнению (1.8):

Следовательно

y_В = 0,187

5. Вычислить состав равновесной паровой фазы при 60⁰С для жидкой смеси, состоящей из 40 мол. % бензола и 60 мол. % толуола. Считать, что данная смесь характеризуется законом Рауля. Найти также, какого состава жидкая смесь бензола и толуола кипит при 90 ⁰С под давлением 760 мм рт.ст.

Решение: давление насыщенного пара бензола и толуола при 60 °С определяем по прил. 16: для бензола Р_Б = 385 мм рт.ст.; для толуола Р_Т = 140 мм рт. ст.

Парциальные давления бензола и толуола определяем по формуле (1.7):

р_Б =Р_Б·х_Б = 385·0,4 = 154 мм рт. ст.

р_Т =Р_Т·х_Т = Р_Т·(1- х_Б ) = 140·0,6 = 84 мм рт. ст.

Общее давление:

П = р_Т + р_Б = 154 + 84 = 238 мм рт. ст.

Состав паровой фазы определяем по формуле (1.8):

.

Итак, равновесный пар содержит 64,8 мол. % бензола и 35,2 мол. % толуола.

Для определения состава жидкости, кипящей под давлением 760 мм рт. ст. при 90 ⁰С, напишем два уравнения6

П = р_Т х_Т + р_Б х_Б или 760 = 408 х_Т ·1013 х_Б

х_Т + х_Б = 1

Здесь 1013 и 408 – давления насыщенного пара чистых бензола и толуола при 90⁰С, мм рт.ст.

Решая систему уравнений, получим:

х_Б = 58,3 % х_Т = 41,7%

Контрольные задачи.

1. Выразить концентрации питания, дистиллята и кубового остатка в мольных долях:

Жидкая смесь содержит 40 масс. % бензола и 60 масс. % толуола. Требуемое содержание бензола в дистилляте 96 масс. %, требуемое содержание толуола в кубовом остатке 98 масс. %. Исходная смесь перед подачей в колонну подогревается до температуры кипения.

Ответ: x_F = 0,44, х_D = 0,965, х_W = 0,023.

2. Смешаны два равных объема бензола и нитробензола. Считая, что объем жидкой смеси равен сумме объемов компонен­тов, определить плотность смеси, относительную массовую концентрацию нитробензола и его объемную мольную концентра­цию С_Х.

Ответ: ρ_СМ = 1050 кг/м³; кг нитробензола/кг бензола.

3. Состав жидкой смеси: хлороформа 20%, ацетона 40%, сероуглерода 40%. Проценты мольные. Определить плотность смеси, считая, что изменения объёма при смешении не происходит.

Ответ: 1143 кг/м³.

4. Воздух насыщен паром этилового спирта. Общее давление воздушно – паровой смеси 600 мм рт.ст., температура 60 °С. Принимая оба компонента смеси за идеальные газы, определить относительную массовую концентрацию 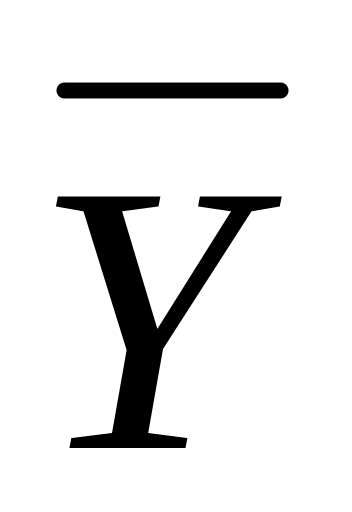этилового спирта в смеси и плотность смеси.

Ответ: 1,59 кг спирта/кг воздуха; ρ_СМ = 1,08 кг/м³.

5. Газ состава: водород 26%, метан 60%, этилен 14% (проценты мольные) имеет давление р_АБС = 30кгс/см² и температуру 20 °С. Считая компоненты смеси идеальными газами, определить их объёмные массовые концентрации 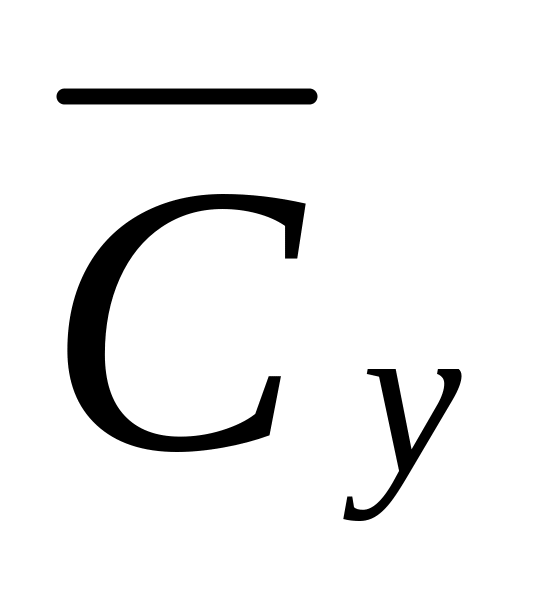(в кг/м³).

Ответ: 0,634 кг/м³ водорода, 11,59 кг/м³ метана, 4,74 кг/м³ этилена.

6. Рассчитать коэффициенты молекулярной диффузии под атмосферным давлением а) пара бензола в паре толуола при тем­пературе 100 °С; б) пара этилового спирта в водяном паре при температуре 92 °С.

7. Смесь бензола и толуола кипит при 95 °С под давлением 760 мм рт. ст. При 95 °С давление насыщенного пара бензола Р_Б = 1167 мм рт. ст.; давление насыщенного пара толуола Р_Т = 480 мм рт. ст. Найти состав кипящей жидкости, считая, что данная смесь характеризуется законом Рауля.

Если жидкость будет содержать в два раза меньше толуола, то под каким давлением она будет кипеть при той же температуре?

Ответ: х_Б = 0,408, П = 962 мм рт.ст. = 128,3 кПа.

8. Если жидкость будет содержать в два раза меньше толуола, то под каким давлением она будет кипеть при той же темпера­туре?

9. Определить равновесные составы жидкости и пара для смеси метиловый спирт—вода при температуре 50 °С: а) под давлением 300 мм рт. ст., б) под давлением 500 мм рт. ст., считая, что смесь характеризуется законом Рауля. Объяснить полученный для случая б) результат.

Ответ: а) х = 0,675, y* = 0,9; б) при 50 °С давление не может превышать 400 мм рт. ст.

10. Построить кривую равновесия при общем давлении 2 aт для смеси гексан—гептан, считая приложимым закон Рауля. Давления насыщенных паров чистых компонентов взять по номограмме (прил. 15).

11. Определить состав равновесного пара над жидкой смесью состоящей из 10 мол. % воды, 50 мол. % уксусной кислоты и 40 мол. % ацетона при t = 80 °С, считая, что смесь характеризуется законом Рауля.

Ответ: 4,2 % (мол.) воды; 13 % (мол.) уксусной кислоты; 82,8 % (мол.) ацетона.