1.3. Классификация сил (модели нагружения)

При рассмотрении любой детали или сооружения взаимодействие с окружающими ее элементами и воздействие внешней среды характеризуется внешними силами. Классификация их представлена на рис.1.5.

Внешние силы

Поверхностные

Объёмные

Распределённые

Сосредоточенные

[Н, кН]

по длине

[Н/м, кН/м, кН/см]

по поверхности

[Н/м², кН/см²]

Рис.1.5

1кгс = 9,81Н  10Н; 1Н/м² = 1Па;

1тс = 9,8кН  10кН; 10⁶Па = 1МПа.

Сосредоточенные силы – силы, действующие на небольших участках поверхности деталей (например, давление колеса на рельсы, давление моста на опору).

Распределённые силы – силы, приложенные к значительным участкам поверхности (например, давление жидкости или газа на стенки сосуда).

Объёмные или массовые силы – силы, приложенные к каждой частице материала (например, силы тяжести или силы инерции).

Важным моментом при разработке модели нагружения является учёт характера изменения внешних сил по времени. Классификация на рис.1.6.

Рис.1.6

Стационарные или статические силы нагружают конструкцию медленно, постепенно возрастая от нуля до своего конечного значения. По достижении конечного значения не меняются. Ускорения элементов конструкций равны нулю.

Циклические или повторно – переменные нагрузки многократно меняют свою величину и направление по периодическому закону. Такие нагрузки испытывают вращающиеся валы машин.

Динамические нагрузки меняют свою величину в течение малого промежутка времени и сопровождаются значительными ускорениями, например, ударное нагружение, возникающее вследствие резкой остановки вращающегося массивного вала машины.

а б

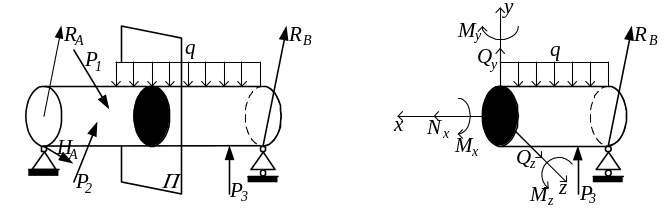
Деталь Отсечённая часть детали

Рис.1.7

Детали находятся в равновесии под воздействием приложенных к ним внешних сил (рис.1.7,а). Реакции опор также относятся к внешним силам. Взаимодействие между частями рассматриваемой детали характеризуется внутренними силами. Чтобы обнаружить внутренние силы, необходимо провести плоскость, которая рассечёт деталь на две части и рассмотреть равновесие любой из них (рис.1.7,б)

Внутренние силы в сечении П представляют собой силы взаимодействия между частицами материала. Из условий равновесия (1.1.) отсечённой части тела можно определить составляющие главного вектора и главного момента внутренних сил, действующих в сечении П. В этом состоит сущность метода сечения – одного из важных методов сопротивления материалов.

∑х = 0, ∑у = 0, ∑z = 0, ∑M_x = 0, ∑M_y = 0, ∑M_z = 0. (1.1)

Составляющие (компоненты) внутренних сил имеют следующие названия:

N_x – продольная сила;

Q_y и Q_z – поперечные силы;

M_x – крутящий момент;

M_y и M_z – изгибающие моменты.

Распределение внутренних усилий по сечению заранее неизвестно, определение его составляет одну из главных задач сопротивления материалов.