1.9 Построение графика приведённого к ведущему звену момента инерции механизма в зависимости от угла поворота звена

К инетическая энергия звена движущегося поступательно равна:

(17)

где v_s – скорость центра масс звена,

m – масса звена.

Кинетическая энергия звена движущегося вращательно равна:

(18)

где I_s – момент инерции звена относительно оси вращения, проходящей через центр масс.

ω – угловая скорость звена.

Кинетическая энергия звена движущегося сложно равна:

(19)

Получаем выражение для приведённого момента инерции:

Для первого положения приведенный момент инерции равен:

φ	1	2	3	4	5	6	7	8	9	10	11	12
Jsn	2,95	2,38	1,57	1,6	3,93	6,85	4,01	1,57	1,55	2,34	2,84	3,21

Для построения графика приведённого к ведущему звену момента инерции данного механизма ось ординат направим горизонтально, т.е. стоим график повернутый на .

Масштабный коэффициент:

.

1.9 Построение диаграммы «энергия-масса»

Диаграмма «энергия-масса» строится путём графического исключения параметра из графиков и , т.е. построение идёт по точкам, полученным при пересечении линий переноса ординат точек соответствующих положений механизма кривых и . График имеет вид замкнутой кривой.

1.10 Определение момента инерции маховика, обеспечивающего вращение звена приведения с заданным коэффициентом неравномерности движения при установившемся режиме работы

Для определения величины момента инерции необходимо провести касательные к графику «энергия-масса» под углами и к оси абсцисс, тангенсы которых определяем по формулам:

, (20)

, (21)





Искомый момент инерции найдём из выражения:

, (22)

где  отрезок, отсекаемый проведёнными касательными на оси ординат диаграммы «энергия-масса», мм.

Тогда

.

1.11 Определение геометрических размеров маховика

К геометрическим размерам маховика относят диаметр и ширина обода маховика. Из конструктивных соображений примем ширину обода маховика .

Диаметр определим по формуле:

, (23)

где  удельная масса материала маховика ( ).

.

2. Силовой расчёт рычажного механизма с учётом динамических нагрузок

Силовой расчет механизма будет вести для десятого положения.

2.1 Построение не повёрнутого плана скоростей

Не повёрнутый план скоростей механизма для третьего положения строится аналогичным образом, как и повернутый, с условием реальных направлений скоростей, а не повернутых на 90°.

2.2 Построение плана ускорений

Т ак как частота вращения ведущего звена n₁=const , то точка А₁ имеет только нормальное ускорение:

(24)

Вектор изображающий ускорение a₁ принимаем равным 100 мм.

Найдём масштабный коэффициент для построения плана ускорений:

Этот вектор направлен к центру вращения , т. е. от точки А₁ к точке О₁, параллельно звену О₁А₁.

Ускорение точки А₃ определяется системой из двух векторных уравнений:

(25)

Ускорение равно 0.

Определим значение нормальной составляющей ускорения точки А₃:

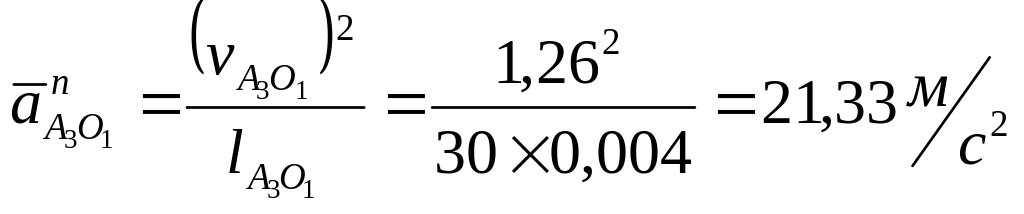
(26)

С учётом масштабного коэффициента находим значение данного ускорения на плане ускорений:

Определяем значение ускорения Кориолиса:

(27)

С учётом масштабного коэффициента:

Проводим вектор параллельно звену 3. Получаем точку n₃. Из точки a проводим вектор , направление которого получаем путем поворота на 90° в сторону вращения звеньев механизма скорости V_A3A. Перпендикулярно вектору проводим вектор . Из точки n₃ проводим вектор . Точка пересечения векторов и дает нам точку а₃. Соединяя точку а₃ с полюсом получим вектор ускорения точки А лежащей на звене 3.

Ускорение точки В определятся из следующего соотношения:

Ускорение точки С определяется системой из двух векторных уравнений:

(28)

Нормальная составляющая ускорения точки С относительно точки В определяем из выражения:

(29)

С учётом масштабного коэффициента:

Полное ускорение точки С получим соединив точку c на плане ускорений с полюсом:

(30)

Находим ускорения центров тяжести:

(31)4

Найдём полное ускорение точки S₄:

(32)

Через точку b проводим вектор параллельно звену 4, получаем точку n₄. Через эту точку проводим прямую перпендикулярную вектору . Из полюса проводим прямую параллельную оси х – х. Пересечение этих прямых дает точку с. Соединяя точку с с полюсом получаем вектор ускорения точки С. Точка S₄ лежит на расстоянии 0,5 от точки b, прямой bc. Соединяя с полюсом эту точку получаем ее ускорение.

Ускорения определенные математически из плана скоростей сведем в таблицу 6.

^{Таблица 6 – Значения ускорений точек механизма, м/с}2

29,64	45,6	14	23,2	46,056	45,83	46,5