Цепи с взаимной индуктивностью

Индуктивно связанные элементы цепи

Если изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции.

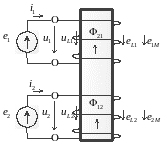
Рисунок 4.1- Схема с индуктивно связанными элементами цепи

e_L1, e_L2 - ЭДС самоиндукции;

e_1M, e_2M - ЭДС взаимной индукции;

Ф₁₂ - поток взаимной индукции, создаваемый i₁ и наводящий ЭДС e_2M;

Ф₂₁ - поток взаимной индукции, наводящий ЭДС e_1M (создаваемый i₂).

Направление магнитного потока определяется по правилу правого винта:

В данном примере катушки имеют одинаковые направления намотки. На обычных схемах направление витков катушек не указывают, но помечают их одноименные зажимы точками. Одноименными называют такие зажимы, по отношению к которым одинаково ориентированные токи создают одинаково направленные потоки самоиндукции и взаимной индукции. Токи и наведенные ими ЭДС взаимной индукции направлены от одноименных зажимов катушек.

Различают два вида включения катушек: согласное и встречное. Согласным называют такое включение, при котором потоки самоиндукции и взаимной индукции катушек имеют одинаковое направление. Если направления потоков противоположны, то включение катушек называется встречным.

Наличие взаимной индукции обозначают дугой со стрелками и буквой М. Магнитная связь катушек характе-ризуется коэффициентом взаимной индукции М [Гн].

r₁, r₂ - активные сопротивления катушек (сопротивление использованных проводов).

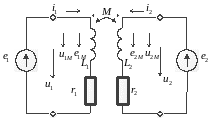
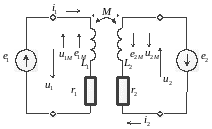
а)                                              б)

а - согласное включение; б - встречное включение

Рисунок 4.2 - Способы включения катушек со взаимной индуктивностью

Уравнение электрического состояния двух цепей с магнитной связью

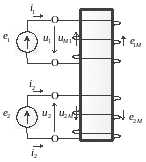
Рисунок 4.3 - Схема двух цепей с магнитной связью

По второму закону Кирхгофа записываем уравнение для каждого контура:

;                (4.1)

                                         .

Если токи синусоидальные, то в катушках наводится:

;                        (4.2)

.

ЭДС взаимной индукции:

;    (4.3)

.

; .            (4.4)

ЭДС, наводимая током, отстает от него на угол π/2. Величину ω∙M называют реактивным сопротивлением взаимной индуктивности катушек x_M:

,                                       (4.5)

Если токи обмоток записать в комплексной форме:

;   ,                      (4.6)

то комплексные значения ЭДС взаимной индукции выразятся так:

;(4.7)

.

Напряжение, компенсирующие ЭДС взаимной индукции связаны с токами следующими уравнениями для согласного и встречного включения одинаково:

;                     (4.8)

                        .

Уравнения электрического состояния катушек с взаимной индуктивностью при согласном встречном включении:

;                     (4.9)

                               .

Знак <+> при согласном, знак <-> при встречном включении катушек:

;

.

Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи:

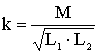, .               (4.10)

Эквивалентная замена индуктивных связей

Электрическая цепь, содержащая взаимные индуктивности, может быть упрощена, если воспользоваться приемом, который называется устранение или развязка индуктивных связей. Им можно воспользоваться только, если катушки присоединены к общему узлу. Возможно два случая: катушки соединены одноименными выводами или разноименными выводами.

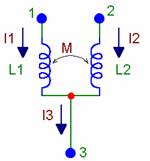
Рисунок 4.4 - Присоединение катушек с взаимной индуктивностью присоединенных к общему узлу

;

;

.

Верхние знаки - когда одноименные соединены. Нижние - когда разноименные.

Исключаем из первого уравнения I₂, а из второго I₁:

;

;

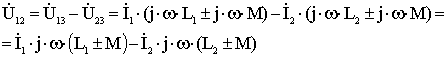
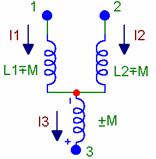
Рисунок 4.5 - Эквивалентная схема замещения для катушек с взаимной индуктивностью, присоединенных к общему узлу

Последовательное соединение индуктивно связанных элементов цепи

а)

б)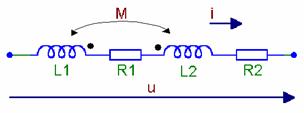

а - согласное включение; б - встречное включение

Рисунок 4.6 - Последовательное соединение катушек индуктивности

Эквивалентная индуктивность:

.                    (4.11)

<+> - согласное, <-> - встречное.

В идеальном случае (k=1):

.

Если, кроме того, L₁ = L₂, то при согласном включении:

_,

при встречном включении:

.

Входное сопротивление всей цепи:

.                    (4.12)

Параллельное соединение индуктивно связанных элементов цепи

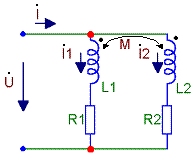
Рисунок 4.7 - Параллельное соединение катушек индуктивности

Введем обозначения:

;

;

.

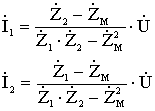
[одноименные соединения]       (4.13)

Вывод: при параллельном соединении эквивалентное сопротивление меньше меньшего из сопротивлений, однако несколько больше эквивалентного сопротивления при отсутствии взаимной индукции - при  одноименном соединении и меньше - при разноименном.

Воздушный трансформатор (без стального магнитопровода)

Трансформаторы применяются в электротехнике для преобразования переменного напряжения. Обмотка, к которой подводится питание, называется первичной, обмотка, к которой присоединяется приемник энергии - вторичной. Цепи, в состав которых входят первичная и вторичная обмотки трансформатора, называются соответственно первичной и вторичной цепями трансформатора.

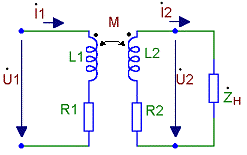
Рисунок 4.8 - Первичная и вторичная цепи воздушного трансформатора

, , ,  ,

R₂₂ и x₂₂ - активное и реактивное сопротивления вторичного контура.

,

.

Решаем относительно İ₁:

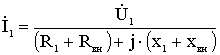,              (4.14)

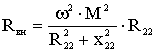.                 (4.15)

R_вн и x_вн - вносимые (из второго контура в первый) активное и реактивное сопротивления:

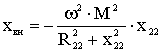                  (4.16)

Т.о. со стороны первичной обмотки вся схема может рассматриваться как двухполюсник с сопротивлением:

.

Вносимое активное сопротивление всегда больше нуля. В нем поглощается энергия, которая в реальной цепи передается из первичной цепи во вторичную. Вносимое реактивное сопротивление имеет знак, противоположный знаку x₂₂.