
- •5. Переходные процессы в линейных электрических цепях (постоянного тока – занятие 5, переменного тока – занятие 6)
- •5.1. Основные теоретические сведения
- •4.2. Примеры решения
- •3.2.1. Решение задачи классическим методом
- •1. Расчет переходных процессов на постоянном токе
- •1.1 Классический метод
- •2. Расчет переходных процессов на переменном токе
- •2.1.Классический метод
2. Расчет переходных процессов на переменном токе
Когда ток в индуктивности и напряжение на емкости достигнут установившегося значения при работе электрической цепи в рассмотренном выше режиме, срабатывает ключ К2 (К1остается в положении предшествующего режима). Электрическая цепь на рис. 9 подключается к источнику энергии переменного напряжения. Ток от источника постоянного напряжения будет замыкаться только через ветвь с идеальным источником напряжения е(t), обладающим нулевым внутренним сопротивлением. На переходной процесс в остальной цепи ЭДС постоянного напряжения влиять не будет. Электрическая цепь, в которой будет происходить переходной процесс представлена на рис.9.

Рис.9
2.1.Классический метод
Решение
Ток в индуктивности после коммутации является решением дифференциального уравнения первого порядка и представляет собой сумму двух составляющих:
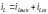 ,
,
где
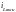 ̶
вынужденная составляющая, значение
тока в новом установившемся режиме .
̶
вынужденная составляющая, значение
тока в новом установившемся режиме .
Так как в цепи действует источник энергии синусоидального напряжения, электрическая цепь линейная, то тоже изменяется по гармоническому закону.
По закону Ома в комплексной форме:
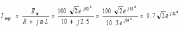 ,
А
,
А
Напряжение на индуктивности в установившемся состоянии (принужденная составляющая):
 , В
, В
Мгновенные значения принужденных составляющих тока и напряжения на индуктивности:
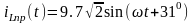 .
А
.
А
 ,В
,В
Свободная составляющая
тока не зависит от напряжения источника
и имеет вид:
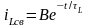
При этом постоянная времени цепи на рис.9.
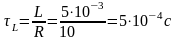
 1/c
1/c
Значение тока в индуктивности в переходном процессе:
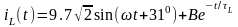 (2.1)
(2.1)
Для определения постоянной интегрирования В в выражение (2.1) подставим t = 0+
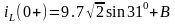
Согласно первому закону коммутации
 ,
,
где - установившееся значение тока в индуктивности в предшествующем режиме работы электрической цепи определяется выражением (1.4), т.е.
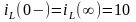 ,
А
,
А
Значение постоянной
 ,
А
,
А
Закон изменения тока в индуктивности в переходном процессе имеет вид:
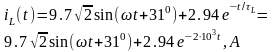
Напряжение на индуктивности :
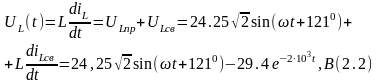
Графики
и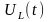 приведены на рис.10. и рис.11.
приведены на рис.10. и рис.11.
Для построения графиков
определим, сколько
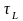 содержится в периоде гармонической
функции Т.
содержится в периоде гармонической
функции Т.
Период
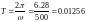 с.
с.
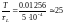 ,
,
т.е. в отрезке длиной Т(3600) содержится 25 .
Результаты вычислений для построения графиков сведены в таблицу 2.
t |
|
,А |
|
,А |
|
В |
В |
τ |
0.37 |
0.77√2 |
7√2 |
7.77√2 |
7.7√2 |
17.2√2 |
9.5√2 |
2τ |
0.14 |
0.29√2 |
8.5√2 |
8.79√2 |
2.9√2 |
12.1√2 |
9.2√2 |
3τ |
0.15 |
0.1√2 |
9.4√2 |
9.5√2 |
√2 |
6.3√2 |
5.3√2 |
4τ |
0.02 |
0.04√2 |
9.7√2 |
9.74√2 |
0.4√2 |
0 |
-0.4√2 |
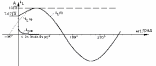
Рис.10
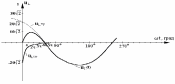
Рис.11
2.2. Решим эту же задачу операторным методом.
Так как в рассматриваемом случае действует синусоидальная ЭДС e(t), то расчет операторным методом значительно упрощается, если оперировать с мгновенной комплексной ЭДС
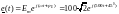 ,
В,
,
В,
изображение которой имеет вид (см. приложение 1 п.5)
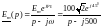
Для
учета ненулевых начальных условий
фиктивную ЭДС
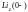 умножим на ,,j'',тогда
операторная схема имеет вид:
умножим на ,,j'',тогда
операторная схема имеет вид:
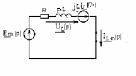
Рис.12
Применяя
метод наложения, определим
 :
:
 (2.3)
(2.3)
После подстановки численных значений выражение (2.3) принимает вид:

Найдем комплексный оригинал тока с помощью теоремы разложения.
Определим корни знаменателя.
F2(p) = 0 (p-j500)(10+5·10-3·p) = 0
откуда

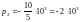
Производная по p от знаменателя F2(p) имеет вид :

Подставим значения корней р1 и р2 в выражения F1(p) и F'2(p):
 ;
;
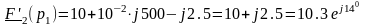 ;
;
 ;
;
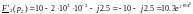 ;
;
Комплексный оригинал тока в индуктивности имеет вид:
 .
.
Искомый ток представляет собой мнимую часть последнего выражения:

Напряжение на индуктивности согласно II закону Кирхгофа в операторной форме имеет вид (рис.12):
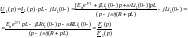
Определим
оригинал
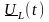 по теореме разложения.
по теореме разложения.
Корни
знаменателя определены выше :
и
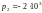
Вычислим F1(p1) и F1(p2):
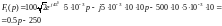
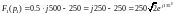
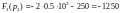
Выражения для F'2(p1) и F'2(p2) получены раньше.
Комплексный оригинал напряжения на индуктивности:
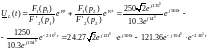
Искомое напряжение на индуктивности в переходном процессе является мнимой частью комплексного оригинала:

Таким образом, расчеты проведены верно, т.к. ток и напряжение на индуктивности, определенные разными методами имеют одинаковые выражения.
Цель работы: расчет домашнего задания по теме «переходные процессы на постоянном и переменном токе»
Содержание задания
Рассчитать переходные процессы в разветвленной электрической цепи классическим и операторным методом при двух коммутациях:
1. на постоянном токе при срабатывании ключа К1 ( ключ К2 остается в положении, изображенном на схеме );
2. на переменном токе при срабатывании ключа К2 (ключ К1 остается в положении соответствующем п1).
Причем ключ К2 замыкаем в тот момент , когда переходной процесс от замыкания ключа К1 закончился.
В каждом из указанных
случаев необходимо определить и построить
графики
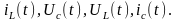
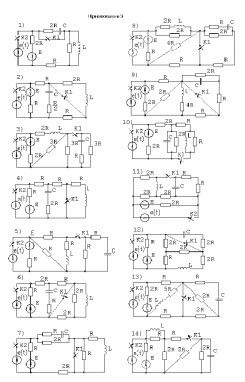
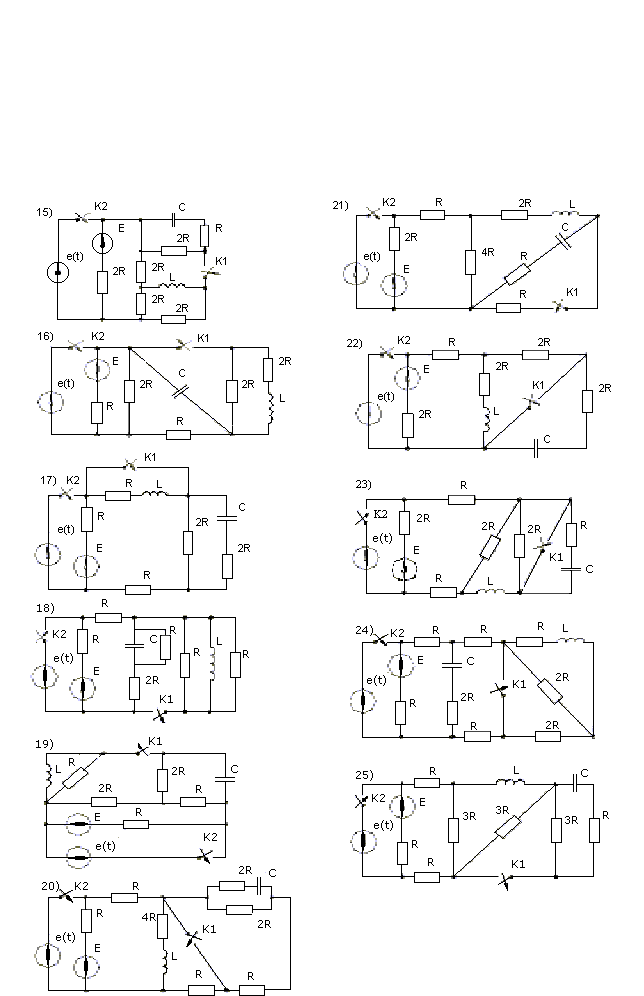
Исходные данные для расчета и схемы приведены в приложениях 2и 3.Номер варианта задает преподаватель .
Номера вариантов, численные значения и расчетные схемы приведены в приложениях 2 и 3.
Список литературы:
1. Г.В.Зевеке, П.А. Ионкин и др. Основы теории цепей М: 1989г. стр. 234-288.
2. М.Р. Шебес, Теория линейных электрических цепей в упражнениях и задачах. М: Высшая школа 1967 стр. 335-399.
3. Бессонов А.А. Теоретические основы электротехники, электрические цепи. М: Высшая школа, 1984
4. Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи. М: Энергия, 1978.
Дана электрическая цепь в которой происходит коммутация (рис. 2.6 -2.10). В цепи действует постоянная ЭДС Е. Параметры цепи даны в таблице 2.2.
Определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения на каком-либо элементе.
Задачу решить двумя методами: классическим и операторным. Построить график переходного процесса для искомой величины на интервале от t = 0 до t = 3max.
Таблица 2.2
Приложение 2

№ вар |
Рис |
Е, В |
L, мГн |
С, мкФ |
R1 |
R2 |
R3 |
R4 |
Опреде-лить |
|||
Ом |
|
|||||||||||
1 |
2.1 |
100 |
1 |
10 |
50 |
25 |
25 |
- |
uc |
|||
2 |
2.2 |
100 |
1 |
10 |
50 |
20 |
30 |
- |
иL |
|||
3 |
2.3 |
100 |
1 |
10 |
20 |
15 |
5 |
2 |
i |
|||
4 |
2.4 |
100 |
1 |
10 |
20 |
2 |
18 |
2 |
uc |
|||
5 |
2.5 |
200 |
1 |
10 |
10 |
25 |
50 |
15 |
i3 |
|||
6 |
2.6 |
200 |
1 |
10 |
10 |
30 |
50 |
10 |
uL: |
|||
7 |
2.7 |
50 |
2 |
167 |
1 |
2 |
2 |
4 |
i2 |
|||
9 |
2.8 |
150 |
4 |
5 |
6 |
10 |
5 |
4 |
uc |
|||
10 |
2.9 |
150 |
4 |
5 |
3 |
10 |
5 |
7 |
i2 |
|||
2.10 |
|
|
|
|
|
|
|
|
|
|||
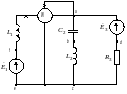
Рис. 2.1.
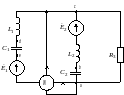
Рис. 2.2.
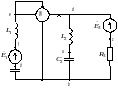
Рис. 2.3.
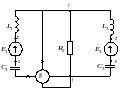
Рис. 2.4.
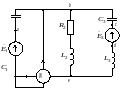
Рис. 2.5.
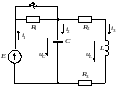
Рис. 2.6.

Рис. 2.7.
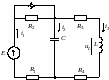
Рис. 2.8.

Рис. 2.9.
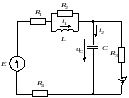
Рис. 2.10.
3.2. Расчет переходного процесса в линейной электрической цепи
5.15. Дано: i(t)=0,4sin(314t+90o) A ; R=R1=800 Oм, C=10мкФ.
О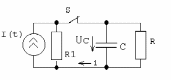 пределить
напряжение на емкости Uc
и ток i
после коммутации.
пределить
напряжение на емкости Uc
и ток i
после коммутации.
.
C
= 2 мкФ. Найти
напряжение на емкости UC
после коммутации.
S
C
R1
i
UC
R











e(t)

5.17. E=180 В; R1=240 Ом; R2 = 120 Ом; C = 25мкФ.
Определить
напряжение Uc
и токи i1
и i2
после коммутации.


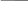


i1
R1

 S
S


 C
Uc
C
Uc

 E
E
 R2
R2

 i2
i2


R2 = 30 Ом.
Определить:
ток i и Uc после коммутации;
ток i*.

R1 C L
S
R2
e(t)
i*
i
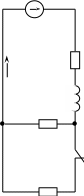
5.19. Ключ S размыкается в момент, когда синусоидальный ток i в цепи имеет максимальное значение 100 А.
Найти ток i в цепи после коммутации, если L=100 мГн, R1=1 Ом,
R2=9 Ом, R3=1,12 Ом, f=50 Гц.
i
S
R3
R2
L
R1

e(t)
5.20. Дано: Е1=100 В, Е2=400 В, R1=100 Ом, R2=50 Ом, C=30 мкФ.

S
R2
C
Определить: Uс после коммутации.
Е2
Е1

R1
Определить
токи I1
I3
при переходном процессе; Решить
задачу при перемене местами L
и C.
5
 .21.
Дано:
Е=200 В, R=25
Ом, С=50 мкФ, L=166,6
мГн.
.21.
Дано:
Е=200 В, R=25
Ом, С=50 мкФ, L=166,6
мГн.
5.22. Дано: E=100В; R=50 Ом; L=58,75 мГн; С=100 мкФ
О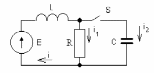 пределить
токи i1-i3,UC
и UL
пределить
токи i1-i3,UC
и UL
при переходном процессе.

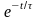
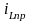 ,А
,А ,В
,В ,
,