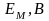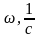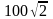- •5. Переходные процессы в линейных электрических цепях (постоянного тока – занятие 5, переменного тока – занятие 6)
- •5.1. Основные теоретические сведения
- •4.2. Примеры решения
- •3.2.1. Решение задачи классическим методом
- •1. Расчет переходных процессов на постоянном токе
- •1.1 Классический метод
- •2. Расчет переходных процессов на переменном токе
- •2.1.Классический метод
4.2. Примеры решения
Пример
1. Определить
закон изменения напряжения на конденсаторе
C
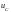 и тока
и тока
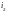 электрической
цепи, приведенной на рис. 1, при
электрической
цепи, приведенной на рис. 1, при
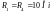 ,
,
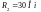 ,
,
 ,
,
 ,
,
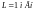 ,
,
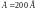 .
.

Рис. 1
3.2.1. Решение задачи классическим методом
Составим характеристическое уравнение

![]()
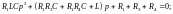
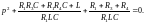
Подставив численные значения, получим:
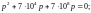
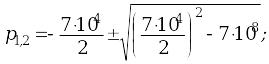


Корни
характеристического уравнения
действительные и различные - переходный
процесс апериодический и общее решение
для
 и
имеет вид:
и
имеет вид:
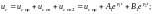

где
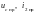 - принужденные (установившиеся) значения
- принужденные (установившиеся) значения
 и
.
и
.
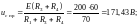

Найдем
постоянные интегрирования
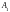 и
и
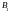 .
На основании второго закона коммутации
.
На основании второго закона коммутации
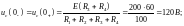
Для
момента



 (*)
(*)
Для составления второго уравнения для и найдем
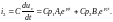
Вычислим
ток
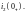
По
первому закону Кирхгофа
 .
В этой формуле для тока
.
В этой формуле для тока
 должен выполняться первый закон
коммутации:
должен выполняться первый закон
коммутации:
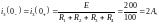
а
ток
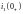 найдем, используя второй закон Кирхгофа
для левого контура (рис. 3.4.):
найдем, используя второй закон Кирхгофа
для левого контура (рис. 3.4.):
 ,
откуда
,
откуда
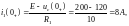
тогда
 и
и

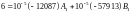 (**)
(**)
Объединяя уравнения (*) и (**) в систему, получим:
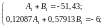

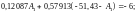

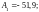



Округляя, получим
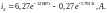
Ответы:
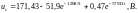
![]()
3.2.2. Решение задачи операторным методом
Составим операторную схему замещения (рис. 3.5).
К ак
видно из схемы, для нахождения
ак
видно из схемы, для нахождения
 целесообразно использовать метод двух
узлов. Заземлив узел 2, для узла 1 составим
уравнение:
целесообразно использовать метод двух
узлов. Заземлив узел 2, для узла 1 составим
уравнение:
 ;
;
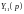 -
узловая проводимость:
-
узловая проводимость:

 -
узловой ток:
-
узловой ток:
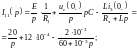
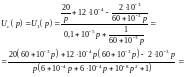
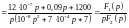 .
.
Для перехода от изображения к оригиналу используем вариант формулы разложения, когда в знаменателе присутствует нулевой корень.
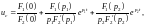
где
 и
и
 - корни уравнения
- корни уравнения
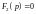
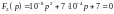
Уравнение совпадает с характеристическим уравнением в классическом методе, его корни:
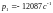 ,
,
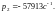
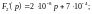

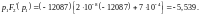

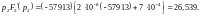
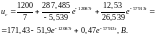
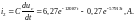
Таким
образом, выражения
и
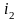 ,
найденные классическим и операторным
методами, полностью совпадают.
,
найденные классическим и операторным
методами, полностью совпадают.
Если
требуется найти только ток
операторным методом, удобнее сразу
получить изображение
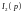 ,
используя закон Ома для второй ветви
(рис. 3.5):
,
используя закон Ома для второй ветви
(рис. 3.5):
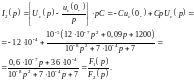
Формула разложения в этом случае имеет вид:
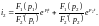

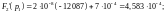

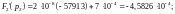
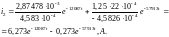
Графики переходного процесса для и построены на рис.3.6. и 3.7.
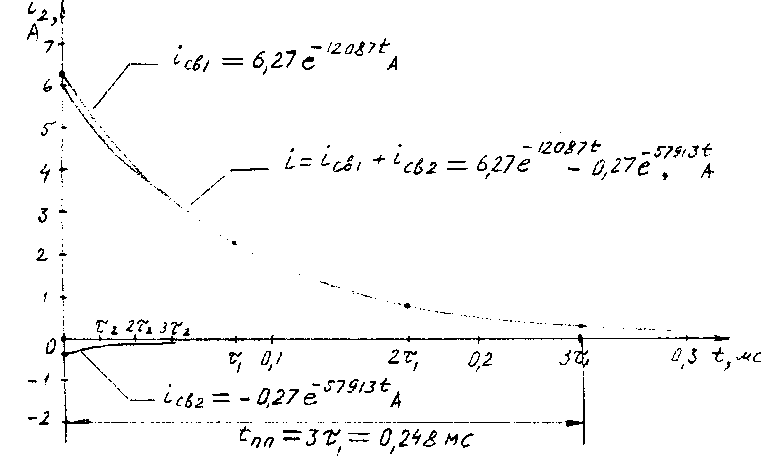
Рис. 3.6.

Пример
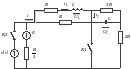
Рис.1
Исходные данные:
Таблица 1
Е, В |
R,Ом |
L, мГн |
С, мкФ |
|
|
|
200 |
10 |
5 |
50 |
|
45 |
500 |
1. Расчет переходных процессов на постоянном токе
При расчете этого режима срабатывает ключ К1, ключ К2 остается в положении, изображенном на схеме.
1.1 Классический метод
Решение
Для цепи до коммутации
(ключ К1 разомкнут) определяем величины
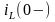 и
и
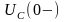 :
:
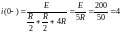 ,А.
,А.
 ,А
(1.1)
,А
(1.1)
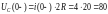 ,В
(1.2)
,В
(1.2)
После замыкания ключа К1 электрическая цепь представляет собой две независимые цепи, в которых происходят переходные процессы.
Одна из них содержит индуктивность и активные сопротивления, другая емкость и активные сопротивления.
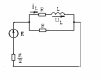
Рис.2
а) Рассмотрим цепь R-L. (рис.2)
Ток в ветви с индуктивностью после коммутации равен:
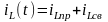 .
(1.3)
.
(1.3)
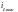 значение тока в новом
установившемся режиме
значение тока в новом
установившемся режиме
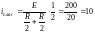 ,
А (1.4)
,
А (1.4)
Свободная составляющая
тока
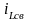 равна:
равна:
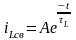 , (1.5)
, (1.5)
где постоянная времени
 ;
;

 ;
;
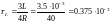 c;
c;
После подстановки выражений (1.4) и (1.5) в (1.3) имеем:
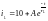 (1.6)
(1.6)
В этом выражении А – постоянная интегрирования. Для ее отыскания воспользуемся начальными условиями коммутации.
Запишем выражение (1.6) для момента времени t = 0+:
 (1.7)
(1.7)
По первому закону коммутации
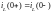 .
.
Так как согласно (1.1)

то и
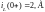
Подставляя значение
 в выражение (1.7)
определяем
постоянную А:
в выражение (1.7)
определяем
постоянную А:
А = 2 -10 = -8, А.
Окончательное выражение
для тока
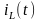 в переходном процессе:
в переходном процессе:
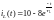 ,
А (1.8)
,
А (1.8)
Значение напряжения на индуктивности в переходном процессе:
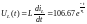 ,
В (1.9)
,
В (1.9)
7:Графики зависимостей
и
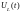 приведены
на рис.3 и рис.4
приведены
на рис.3 и рис.4
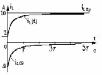

Рис.3 рис.4
б) Рассмотрим цепь R-C, в которой происходит переходной процесс (рис.5)

Рис. 5
Так как в данной цепи отсутствует источник электрической энергии, то напряжение на ёмкости в переходном процессе будет иметь только свободную составляющую, т.е.
 ,
(1.10)
,
(1.10)
а
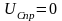 ,
,
где
 ̶
постоянная времени
̶
постоянная времени
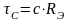 ,
,
 ,
Ом.
,
Ом.
Если подставить в
уравнение (1.10) момент времени t
= 0+, то можно определить значение
постоянной времени В:
 .
.
По второму закону
коммутации
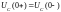 .
.
Согласно выражению (1.2)
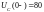 ,
В,
,
В,
тогда
В =80, В.
Закон изменения напряжения на ёмкости в переходном процессе:
 ,
В (1.11)
,
В (1.11)
Ток через емкость в переходном процессе:
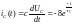 ,
А (1.12)
,
А (1.12)
Графики зависимости
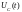 и
и
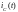 представлены на рис.6 и рис.7:
представлены на рис.6 и рис.7:


Решим эту же задачу операторным методом.
C учетом начальных условий (1.1) и (1.2) операторная схема для цепи после коммутации будет иметь вид:
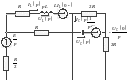
Рис.8
Операторный ток в
индуктивности определим методом
наложения от действия операторной ЭДС
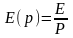 и фиктивной ЭДС, вызванной ненулевыми
начальными условиями в индуктивности
и фиктивной ЭДС, вызванной ненулевыми
начальными условиями в индуктивности
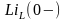 .
т.е.
.
т.е.
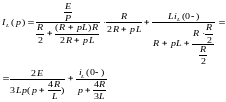
C помощью формул соответствия, приведенных в приложении 1, определяем оригинал тока
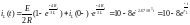 ,
А
,
А
Применяя второй закон Кирхгофа в операторной форме, определяем напряжение на индуктивности:
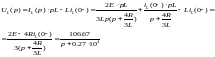
Выражения для UL(p) представляет собой табличную функцию :
UL(p)
= 106.67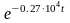 =
106.67
=
106.67 ,
В
,
В
Примечание: В некоторых случаях для определения операторного тока более рациональным является метод эквивалентного генератора, для операторного напряжения – метод узловых потенциалов.
Операторный ток через емкость, как видно из схемы на рис.8, можно определить по закону Ома в операторной форме:
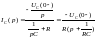 .
.
Выражение для операторного тока IC(p) является табличной функцией:
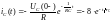 ,
А.
,
А.
Операторное напряжение на емкости имеет вид:
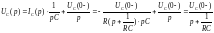
Этому операторному изображению соответствует табличная функция:
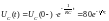 ,
В
,
В
Проведенные расчеты подтвердили правильность решения: законы изменения токов и напряжений в переходном процессе одинаковые при определении разными методами.