7.4. Оптимизация задач распределения инвестиций

Задача 3. Расчет оптимального плана вложения инвестиций

Перед инвестором стоит проблема принятия решения об оптимальном вложении имеющегося у него капитала. Имеется набор характеристик потенциальных объектов для инвестирования, которые имеют условные имена A, B, C, D, Е (см. Табл. 7.2).

Таблица 7.2 - Характеристики потенциальных объектов для инвестиций

Название объектов - Характеристики:	А	В	С	D	Е
Прибыльность (%)	8,0	7,5	5,5	7,0	6,0
Срок выкупа (год)	2012	2019	2017	2016	2015
Надежность (баллы)	2	3	5	4	5

Инвестору, принимая решение о приобретении активов того или иного объекта, необходимо учитывать следующие условия:

1. Суммарный объем капитала, который должен быть инвестирован, составляет $1000000.

2. Часть средств, вложенная в один объект, не может превышать 25% от всего объема капиталовложений.

3. Больше половины всех средств должны быть вложены в долгосрочные активы (например, со сроком погашения после 2015 года).

4. Часть активов предприятий, имеющих надежность (предварительно рассчитанную экспертами) меньше, чем 4 балла, не может превышать трети от суммарного объема инвестиций.

Технология подготовки и решения задачи оптимизации инвестиций

1. Запускаем программу MS Excel и заносим на Рабочий лист данные, необходимые для оптимизации (см. Рис.7.7)

Рис. 7.7. Рабочий лист MS Excel с данными для оптимизации инвестиций

2. В ячейки F3:J3 записываем условные наименования соответствующих объектов для вложения инвестиций - A, B, C, D, E . В ячейку С3 заносим ограничение - суммарный объем капитала для инвестиций - $1000000.

3. В диапазоне ячеек F7: J9 расположены данные - характеристики соответствующих объектов для инвестирования средств.

4. В ячейках D13:D15 записаны формулы заданных в условии ограничений на капиталовложения в те или иные объекты

→D13 = СУММ(F5: J5) →D14 =G5 + H5 + I5

→D15 = F5 + G5 F5: J5 <= 0,25 * $C$3

5. Искомый план вложения инвестиций с точки зрения конкретной целевой функции - максимум надежности инвестиций - располагается в зоне F5: J5, туда заносим начальные нулевые значения х_i..

6. В ячейку K11 (целевая функция) заносим следующую формулу:

=СУММПРОИЗВ (F5: J5;F9: J9) - максимум надежности инвестиций

7. Задаем команду Сервис – Поиск решения. Появившееся диалоговое окно «Поиск решения» (см. Рис.7.8) заполняем следующими данными: целевая функция - $К$11; вид оптимизации - максимальное значение; изменяемые ячейки: $F$5: $J$5.

Вводим ограничения: $F$5: $J$5 – целое,

$F$5: $J$5 < = $F$16, $D$13 = $C$3,

$D$14 >= $F$14 $D$15 <= $F$15

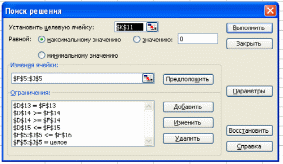
Рисунок 7.8. Диалоговое окно для оптимизации вложения инвестиций

Нажимаем кнопку «Выполнить» и получаем искомые величины (см. Рис.7.9).

Рисунок 7.9. Результат оптимизационных расчетов вложения инвестиций

Возможен и другой вариант решения этой задачи, например, по критерию «максимум рентабельности». В этом случае в технологии решения изменится пункт 6. В ячейку К11 необходимо заносить формулу:

=СУММПРОИЗВ (F5: J5; F7: J7).

Полученные результаты- (см. рис. 7.10.) показывают существенное, по сравнению с первым вариантом постановки задачи, увеличение значения целевой функции.

Рисунок 7.10. Данные для оптимизации по целевой функции

«надежность инвестиций»