
- •Лукашев в.И. Венчурное предпринимательство: Курс лекций. – м.: миит, 2009. – 195 с.
- •Isbn 5-9626-0310-9 © Московский государственный университет путей сообщения (миит), 2009
- •Isbn 978-5-9626-0310-0 в.И. Лукашев, 2009
- •Раздел 1.
- •1.1 Предмет и метод венчурного предпринимательства
- •1.2. История развития венчурного предпринимательства
- •1.3. Проблемы коммерциализации новаций
- •I. Распределение прав на интеллектуальную собственность, созданную при финансовой поддержке государства.
- •II. Следующей центральной задачей является защита интересов государства и исполнителей научно-исследовательских работ.
- •III. Следующим важнейшим моментом является распределение дохода от коммерциализации изобретения.
- •1.4. Организация прямых и венчурных инвестиций
- •1.5. Порядок венчурного инвестирования в инновации
- •Типы инвесторов в зависимости от стадии формирования компании
- •Соотношение рисков и успехов от объёмов инвестиционных вложений
- •Инвестиции в бизнес-проекты большого уровня капитализации
- •1.6. Зарождение российской венчурной деятельности
- •Этапы развития инновационной российской экономики
- •Гносеологические термины и понятия
- •Вопросы для самопроверки
- •Раздел 2. Организация венчурного предпринимательства
- •2.1. Организационно-правовые формы венчурного предпринимательства
- •Возможность смены управляющей компании большинством инвесторов.
- •Соглашение о получении текущих дивидендов/реинвестиции части операционной прибыли, полученной от компаний.
- •2.2. Особенности и формы регистрации венчурных фондов
- •Требования для инвесторов в гк рф
- •2.3. Организация и структура венчурного фонда
- •2.3. Посевное финансирование
- •2.4. Соглашение об инновационном инвестировании
- •2.6. Декларация о намерениях
- •Гносеологические термины и понятия
- •Вопросы для самопроверки
- •Раздел 3. Основы сферы венчурной индустрии
- •Объекты инновационной инфраструктуры, созданные в субъектах Российской Федерации
- •Вопросы для самопроверки
- •Раздел 4. Финансовые основы инвестирования
- •При выдаче ссуды на п лет из условия т погасительных платежей в году последовательные номера месяцев за весь период погашения могут быть записаны в обратном порядке следующим образом:
- •Сумма этих чисел (q) по формуле арифметической прогрессии будет равна:
- •Система неравенств для дисконтных множителей будет иметь вид:
- •Определим приведенную (современную) величину ренты для арифметической и геометрической прогрессии потоков:
- •Вопросы для самопроверки
- •Раздел 5. Методы и инструменты венчурной деятельности. Оценка бизнеса и долей участия
- •Оценочные коэффициенты для Rambler Media и Baidu
- •Результаты оценки «Яндекса» приведены в табл. 5.5.
- •Оценка «Яндекса» на основе рыночных коэффициентов (мультипликаторов)
- •Прогнозируемый денежный поток компании представлен в табл. 5.6.
- •Финансовые результаты реализации венчурного проекта
- •Пример с пут-опционом. Методология соответствует предыдущему примеру при отказе от реализации опциона. Рассмотрим подробнее.
- •Создадим имитирующий портфель безрискового заимствования (ссуды), увязанный с изменением базового актива, для создания денежного потока.
- •Решая систему уравнений, получаем:
- •Определение ставки дисконтирования
- •Ставки дисконтирования в зависимости от стадии развития компании в момент вложений
- •Гносеологические термины и понятия
- •Вопросы для самопроверки
- •Глоссарий и условные обозначения, используемые в венчурном предпринимательстве
- •Литература
- •Д.Э.Н., профессор Лукашев Владимир Иосифович Венчурное предпринимательство: Курс лекций
Пример с пут-опционом. Методология соответствует предыдущему примеру при отказе от реализации опциона. Рассмотрим подробнее.
Опцион на продажу исходит из условия продажи акций лицу, выписавшему опцион. При его реализации курс продажи X = S0 – Р, где X – цена исполнения (X = $590), Р – уплаченная премия (Р = $10), тогда S0 = $600. Условие отказа S0 < S, где S – сложившийся рыночный курс акций в момент завершения проекта.
Так, если приобретен опцион на продажу по цене S0 = $600 за акцию и уплачена премия в размере Р = $10 за акцию, а через год рыночный курс акций составил S = $570, то будет соблюдаться следующее условие:
S0 > S ($600 > $570) отличное от условия отказа.
Поэтому опцион реализуется при курсе продажи акций:
X = S0 – Р = $600 – $10 = $590 за акцию.
Прибыль покупателя опциона составит:
ПР = (X - S) × 1000 акций = ($590 – $570) × 1000 акций = $20 тыс.
Для оценки стоимости простых опционов могут быть использованы различные модели. Наибольшее распространение среди них получили биноминальная модель и модель Блэка-Шоулза.
Биноминальная модель. В основе биноминальной модели оценки опционов (Binomial option pricing model) установление цены опциона основывается на том, что актив в любой период времени может двигаться в одном из двух возможных направлений изменения цен. Общая характеристика процесса изменения цены акции по биноминальной схеме показана на рис. 5.1.
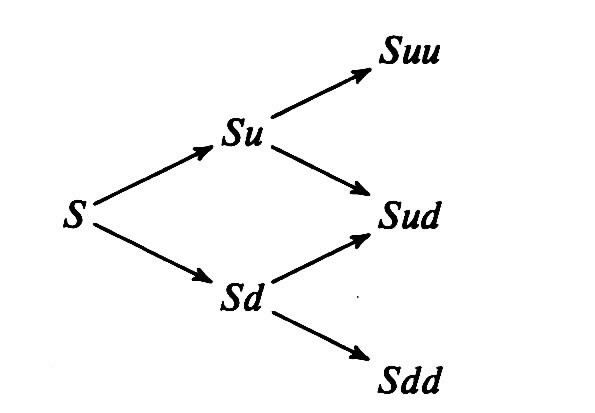
Рис. 5.1.
На рисунке S – текущая цена акции. Цена может либо подниматься до цены Su или Suu с некоторой вероятностью р, либо опускаться до цены Sd или Sdd с вероятностью 1-р. Для определения опциона с помощью арбитражных соображений достаточно использовать шесть компонентов информации: S, u, d, X, r и число периодов n до истечения срока. Помимо S, в качестве компонентов присутствуют: u и d – коэффициенты (мультипликаторы) повышения и понижения цены акции; X – цена исполнения (X = S0 + С); r – безрисковая ставка начисления процентов периода, а R = er - получаемый доход.
Создадим имитирующий портфель безрискового заимствования (ссуды), увязанный с изменением базового актива, для создания денежного потока.
Портфель-имитатор для колл-опциона с ценой исполнения X включает заимствование В (долл.) и приобретение h акций базового актива. Его стоимость в момент 0 равна (hS +B), а величина h называется коэффициентом хеджирования или дельтой (Δ). Стоимость портфеля в момент 1 будет равна либо (hSu + RB), либо (nSd +RB). Основным условием решения является выбор таких величин h и В, чтобы стоимость портфеля в момент 1 была бы равной выплате по колл-опциону:
hSu + RB = Cu и nSd +RB = Cd,
где Cu – стоимость колл-опциона, если цена акции равна Su;
Cd – стоимость колл-опциона, если цена акции равна Sd.
Решая систему уравнений, получаем:
h
=
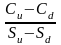 ≥ 0 и B =
≥ 0 и B =
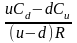 .
.
В биноминальном процессе со многими периодами оценка стоимости опциона должна начинаться с заключительного временного периода и идти назад по времени к текущему моменту (нулевому моменту). Портфели, имитирующие (воспроизводящие) опцион, оцениваются на каждом шаге, что и позволяет выявить стоимость опциона на всех шагах. Заключительный шаг биноминальной модели оценки опциона устанавливает стоимость опциона в единицах имитирующего портфеля, составленного из h акций (Δ акций или дельты опциона) базового актива и безрискового заимствования или ссуды.
Пример. Необходимо оценить колл-опцион с ценой базового актива равной $160 за акцию (S= $600). Изменение цены происходит в соответствии с биноминальным процессом: цена от любого своего значения S может либо возрастать до S×1,5, либо уменьшаться до S×0,5. Ставка непрерывного начисления процентов за период составляет r = 18,232% (r = 0.18232). Оценим Европейский колл-опцион на эту акцию с ценой исполнения в $150 и тремя периодами до окончания срока действия. Изменение цены акции и результат расчета стоимости опциона показаны на рис. 5.2.

Рис. 5.2.
Используемые параметры: S = $160; X = $150; n = 3; u = 1,5; d = 0,5; R = er = 1,2; r = 18,232% или 0,18232; p = 0,7; 1-p = 0,3; h см. табл.5.3.
Как указывалось в условии примера, цена акции биноминально может возрастать, либо уменьшаться в стоимости:
S → Su → Suu → Suuu или $160 → $240 → $360 → $540;
S → Sd → Sdd → Sddd или $160 → $80 → $40 → $20,
а стоимости колл-опциона:
С → Сu → Сuu → Сuuu или $85,069 → $141,458 → $235 → $390,
и иметь промежуточные значения.
Расчет стоимости европейского колл-опциона ведётся по формуле:
С = hS ± B =
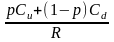 = 0,82031 × $160 - 46,1806 =
= 0,82031 × $160 - 46,1806 =
=
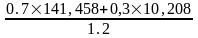 =
=
=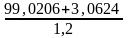 =
=
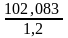 = 85,069.
= 85,069.
Оценка отдельных значений стоимости колл-опциона производится посредством процедуры обратной индукции. Стоимости конечных значений колл-опциона определяются следующим образом:
Сuuu = Suuu – Х = 540 – 150 = 390;
Сuud = Suud – Х = 180 – 150 = 30;
Сudd = Sudd – Х = 60 – 150 => 0;
Сddd = Sddd – Х = 20 – 150 => 0.
Далее используя логику расчёта стоимости колл-опциона для С, определяются и остальные значения.
Расчет производится так:
Сuu =
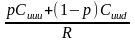 =
=
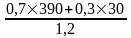 =
=
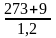 =
235;
=
235;
Сud =
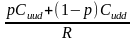 =
=
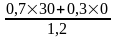 =
=
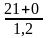 =
17,5;
=
17,5;
Сu =
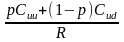 =
=
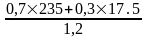 =
=
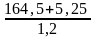 =
141,458;
=
141,458;
Сd =
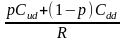 =
=
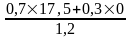 =
=
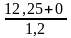 =
10,208.
=
10,208.
Далее, для проведения более детального анализа, рассчитываются вероятности (они могут рассчитываться и на начальной стадии) и значения дельты (h = Δ):
р =
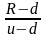 , h =
.
, h =
.
Данные расчета вероятностей и значений дельта приведены на рис. 5.3.

Рис. 5.3
Более сложной для восприятия, но вместе с тем очень широко употребляемой в инвестиционной отрасли, является оценка стоимости опциона по формуле Блэка-Шоулза. Очевидно, что установление цены венчурного проекта будет зависеть не только от внутреннего состояния, но и от внешней среды. В связи с этим реальное значение цены опциона может изменяться непрерывно. Это особенно свойственно акциям и облигациям, цена которых меняется непрерывно даже в течение одного биржевого дня.
Именно в этом случае для определения стоимости опциона с исполнением в конце периода используют формулу Блэка-Шоулза.
Формула Блэка-Шоулза.
Стоимость европейского колл-опциона определяется по формуле:
C(t) = S×F(d1)- Xe-rt×F(d2),
где
d1
=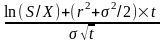 и d2
= d1
-
и d2
= d1
-
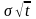
где S - цена базового актива в текущий момент;
X - цена исполнения опциона;
σ - стандартное отклонение цены базового актива;
t – периоды (время) исполнения опциона относительно текущего момента;
r - безрисковая ставка доходности (например, банковская); F(d) - кумулятивная (интегральная) функция нормального распределения.
Пример (источник [Дамодаран]). 26 марта акции Cisco Systems продавались по цене $13,62 (S = $13,62), а 6 июле того же года акции продавались с ценой исполнения $15 (X=$15). Оценить правильность установления размера колл-опциона, если другие параметры составляли:
срок жизни опциона (6 + 30 +31 + 30 + 6 = 103) = 103/365 = 0,2822;
безрисковая ставка = 4,63 (r = 0,0463);
стандартное отклонение σ = 81% (σ = 0,81).
Подставив данные значения в модель, получим:
d1
=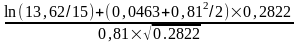 =
=
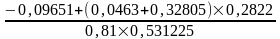 =
=
=
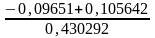 =
=
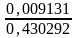 = 0,0212,
= 0,0212,
d2
= d1
-
= 0,0212 – 0,81×
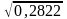 =
=
= 0,0212 – 0,430292 = - 0,4091.
В электронной таблице Exсel найдем значения функции нормального распределения F1(0,0212) и F2(- 0,4091):
F(d1) = 0,508465 = 0,5085; F(d2) = 0,341233 = 0,3412.
Подставив полученные значения в формулу Блэка-Шоулза получим оценку стоимости колл-опциона на акции Cisco с ценой исполнения $15:
С = S×F(d1) - X×e-rt× F(d2) = $13,62×0,5085 - $15×exp(-0,0463×0,2822) ×0,3412 =
= $6,92577 – $15 × 0,999018 × 0,3412 = 6,92577 – 5,113471 = $1,81.
Если учесть, что стоимость опциона в цене исполнения составляла:
$15 – $13,62 = $1,38 < $1,81, то колл-опцион был несколько недооценён.
5.6 Адаптация ДДП к условиям «старт-апа».
Венчурный метод (иначе он называется методом капитализации дохода) является адаптацией метода DCF к случаю старт-апа и учитывает то, что основные объекты венчурного инвестирования – это компании ранних стадий. Определение стоимости компании венчурным методом состоит из следующих шагов:
прогнозируется терминальная стоимость компании на «выходе» - EV (ExitValue);
терминальная стоимость дисконтируется по специальной «венчурной» ставке (до 75 %), учитывающей высокую степень риска π.
Полученная стоимость является стоимостью post-money. Стоимость же pre-money определяют простым вычитанием из нее величины инвестиций Investment. Чаще всего в качестве последнего параметра берется совокупный их объем без учета дисконтирования. Таким образом, имеют место соотношения:
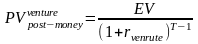
где EV - стоимость компании на «выходе»;
rventure — «венчурный» дисконт, равный rE + π , где имеет порядок 30-40 %;
Т — период до «выхода».
Венчурный метод особенно хорошо подходит, когда понятно, кому, когда и каким образом будет продана доля инвестора в проекте, и сколько можно будет заработать на «выходе». Такой вариант венчурные инвесторы считают самым оптимальным из возможных.
Венчурный метод не учитывает возможные промежуточные дивиденды.
В случае
применения данного метода главным
предметом дискуссии выступает
размер «венчурного» дисконта и премии
за риск π. При
обсуждении
«венчурного» дисконта инвестор может
напомнить, что в нем должны быть учтены
не только возврат и риск, но и стоимость
тех услуг, которые он предоставляет
компании — опыт, связи, репутация,
а также вероятность «разводнения». Это
служит дополнительным аргументом
для повышения![]()
Пример. Рассмотрим вариант оценки компании венчурным методом. «Выход» будет произведен через 4 года, планируемая стоимость компании на «выходе» — $7 млн. инвестиции производятся единовременно в размере $0,5 млн. Менеджеры компании и инвестор пришли к соглашению, что венчурный дисконт rventure для случая компании равен 60 %. Учитывая переменчивость технологического рынка и вероятность понижающего раунда и «разводнения», инвестор и основатели компании согласились на 64 %. Тогда:
=
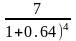 = $0,97 млн.
= $0,97 млн.
Стоимость pre-money в этом случае составила:
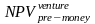 =
=
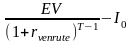 = $0,97 млн. – $0,5 млн. = =$0,47 млн.
= $0,97 млн. – $0,5 млн. = =$0,47 млн.
Преимущество «венчурного» метода — его легкость и традиционное использование многими венчурными инвесторами. «Узкими местами» метода являются следующие обстоятельства:
при выборе коэффициента дисконтирования возможна случайная оценка;
не учитывается возможность досрочного прекращения инвестиций;
не учитывается возможное получение промежуточных дивидендов.
5.7. Определение долей инвестирования
После того, как установлены стоимости компании post и pre-money, представляется возможным произвести расчет долей инвестора, исходя и его вклада.
В качестве простейшей формулы для расчета может быть следующая:
IS
=
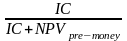 =
=
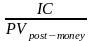 ,
,
где IC – общий размер инвестиций в компанию;
PVpost-money – post-money стоимость компании;
NPVpre-money – pre-money стоимость компании;
IS - доля инвестора.
Пример. IC = $0,5 млн., PVpost-money = $0,97 млн., NPVpre-money = $0,47 млн.,
тогда IS = 0,5 / (0,5 + 0,47) = 0,5 / 0,97 = 51,5%.
Если инвестиции осуществляются в несколько периодов, то они дисконтируются и приводятся к начальному периоду.
При определении доли венчурного инвестора последний часто «страхуется» от «понижающих» раундов и «разводнения», что выражается в увеличении дисконта - премии за риск. Она увеличивает долю венчурного инвестора в компании. Иногда, в случае большой вероятности «понижающего» раунда и «разводнения» доли инвестора, исходную долю инвестора определяют исходя из того, какую долю он хочет сохранить после «разводнения» (IS => CS). Это описывается следующим образом:
CS = SAD × (1+DS),
где CS - доля (в %), передаваемая инвестору в настоящий момент (CurrentShare);
SAD - доля (в %), которую инвестор желает сохранить после «разводнения» (ShareAfterDilution);
DS - количество новых акций, выпускаемых в процессе «разводнения» в % от первоначального количества акций (DilutionShare).
Пример. Согласно полученному ранее результату ее доля равна 51,5 %. Однако инвестору эта доля показалась слишком малой, поскольку он захотел «застраховаться» от разводнения. Было решено, что количество новых акций, выпускаемых для нового инвестора при «разводнении», не превысит 10% от первоначального количества акций.
Тогда, чтобы сохранить долю 51,5 %, инвестор должен получить:
CS = SAD × (1+DS) = 51,5 × (1+0,1) = 56,7.
Таким образом, в итоге доля венчурного инвестора составит 56,7 %.
Альтернативным подходом к определению доли инвестора в компании является сопоставление объема инвестиций и будущей стоимости компании:
IS
=
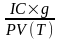 ,
,
где g - ожидаемый рост инвестиций за Т лет;
PV(T) - прогнозируемая post-money стоимость компании через T лет;
IC - инвестиции (может браться как общий объем инвестиций).
Данный метод не учитывает промежуточные дивиденды, если они есть. Если в качестве PV(T) берется значение какого-либо операционного показателя компании (например, один из показателей прибыльности Earning (EBIT, EBITDA) на конец прогнозируемого периода с соответствующим мультипли-катором стоимости компании, то такой метод называется методом «хоккейной клюшки»:
IS
=
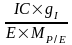 ,
,
где IC – объем венчурных инвестиций, вложенный в реализацию проекта;
g I - темп прироста размера инвестиций по отношению стоимости компании;
E - размер чистой прибыли, полученной через Т лет;
MP/E – мультипликатор, характеризующий отношение цены акции к чистой прибыли компании.
Между параметром gI и ставкой дисконтирования существует прямая связь, которая будет описана ниже.
Пример. Инвестор ожидает рост компании в 3,84 раза (gI = 3,84) за 4 года. Прогнозируемая прибыль компании на «выходе» через 4 года составит $1,3 млн. (Е = 1,3). Мультипликатор Р/Е (отношение цены акции к доходности компании) по результатам оценки акций равен 6. Тогда, в случае использования полного объема инвестиций $1,5 млн., доля инвестора определиться так:
IS
=
=
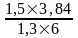 =
=
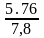 = 0,738 или 73,8%.
= 0,738 или 73,8%.
Доля инвестора составляет 73,8%.
Чикагский метод. Аналогичен предыдущему, с той лишь разницей, что стоимость компании оценивается на основе так называемого кумулятивного эффекта от уровня доходности. При этом рассматриваются различные сценарии получения доходности от инвестиций.
На «входе» в этом методе используются значения Earnings (Е) при различных сценариях и их вероятности, а уже затем рассчитываются их математические ожидания (средние значения). Размером вероятностей для каждого сценария задаются, исходя из реальных текущих условий. Впрочем, «чикагский» метод проигрывает опционному тем, что не учитывает возможность раннего прекращения инвестиций в случае неудачи.
5.8. Эффективность венчурных вложений
Важной задачей для венчурного инвестора является анализ эффективности инвестиций. Суть данной процедуры состоит в сравнении их с альтернативными возможностями вложений.
Рассмотрим простейшую ситуацию, когда инвестор вкладывает в проект А $2 млн., а через год получает отдачу $Z млн. Вложения делаются из расчета 40 % годовых, т. е. инвестор хочет получить как минимум 40 % прибыли через год. На практике это означает, что если менеджеры проекта A данный возврат ему обеспечить не могут, то инвестор найдет возможность вложить средства в другой проект с доходностью, большей или равной 40 %. В рамках этого проекта инвестор может поступить двумя способами.
Рассчитать значение Z-2×(1+0,4) и если данная величина больше или равна 0, то решение об инвестиции будет принято. Можно, «приведя» все к начальному моменту, считать величину -2+
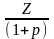 .
.Решить уравнение -2+ =0, если будет p > 0,4, то решение об инвестиции будет принято.
Эти соображения лежат в основе двух наиболее важных методов оценки инвестиций — метода чистой приведенной стоимости NPV (Net Present Value) и внутренней нормы доходности IRR (Internal Rate of Return). Оба метода используют дисконтированный денежный поток. Основные преимущества данных методов заключаются в следующем:
отражение неравноценности разновременных затрат: выгодно более позднее осуществление затрат и более раннее получение финансовых результатов;
учет наличия альтернативной возможности инвестиций;
возможность учета финансового риска.
Внутренняя норма доходности (IRR) представляет собой максимальный уровень цены на капитал (ставки дисконта), при которой проект с заданным потоком средств к инвестору будет представлять для него коммерческий интерес. А именно, если представить NPV как функцию от цены на капитал (ставки дисконтирования), то IRR - это значение, при котором NPV(IRR) = 0. Нахождение IRR осуществляется нахождением решения данного уравнения.
Если r - некоторый дисконт, определяемый инвестором (например, цена акционерного капитала rE с возможной премией за венчурный риск π), то решение об инвестициях принимается, если IRR > r.
Обычно для встречающихся в реальной жизни проектов чаще всего имеет место NPV(rE) > 0 IRR > rE. В силу существующих в инвестиционной (а точнее в банковской) деятельности взглядов, отбор по IRR в настоящее время употребляется чаще, чем по NPV. Вместе с тем, методу IRR присущ ряд недостатков, которые у NPV не проявляются:
если ряд прогнозируемых значений денежных потоков отрицательный, то IRR может не существовать, или же может существовать несколько значений IRR;
если одновременно, за одно и то же время выполняется несколько независимых друг от друга проектов, то их суммарное IRR придется считать отдельно, тогда, как суммарное NPV, можно получить простым сложением.
Остановимся кратко на выборе ставки дисконтирования.
Оценка стоимости проекта методом дисконтированного денежного потока и требует знаний стоимости акционерного капитала. Рыночная стоимость акционерного капитала, как правило, берется равной возможному доходу от альтернативных проектов, которые имеются на рынке в данный момент.
Вместо стоимости капитала имеет смысл рассматривать минимально возможный уровень дохода, желаемый инвестором. Например, если инвестор желает получить от проекта как минимум 40 % годовых, то в роли дисконта нужно положить 40 %. Это означает, что для компании капитал будет стоить 40 % годовых.
На практике инвестор часто руководствуется критерием, что он будет вкладывать средства в проект, если он принесет доходность не менее n раз за k лет, что по сути и является рассмотрением альтернативы: если данный проект не приносит назначенной доходности, то инвестор будет искать другой проект, который эту доходность ему даст, а сформулированный критерий и представляет собой цену акционерного капитала.
Данная формулировка цены акционерного капитала (не менее n раз за k лет) посредством вычислений может быть легко переведена в ставку дисконтирования. Для этого существуют специальные таблицы. Возможные к применению ставки дисконтирования, которые установлены исходя из числовых значений показателей ожидаемого роста стоимости компании, приведены в табл. 5.8. В качестве критериев роста (левый столбец) выбраны те, которые чаще используются для технологических компаний.
Российская Ассоциация Прямого и Венчурного Инвестирования предлагает другой вариант таблицы (табл. 5.9) ставок дисконтирования, наиболее актуальных для России. Здесь в строках показано количество лет, а в столбцах — параметры роста компании.
Таблица 5.8.
Ставки дисконтирования в зависимости от роста
Темп роста |
Ставка дисконтирования (цена акционерного капитала),% |
3 раза за 3 года |
44 |
5 раз за 3 года |
71 |
7 раз за 3 года |
91 |
4 раза за 4 года |
41 |
3 раза за 5 лет |
25 |
5 раз за 5 лет |
38 |
7 раз за 5 лет |
48 |
10 раз за 5 лет |
58 |
Источник: [10]. |
|
Таблица 5.9.
