Определим приведенную (современную) величину ренты для арифметической и геометрической прогрессии потоков:

для потока арифметической прогрессии		для потока геометрической прогрессии
A = ∙ - ;		A = = = ;
Определим наращенные суммы обоих рент, умножив каждое значение А на (1+ i)n, получим:
S = ∙ - ;	S = ;
где и - табулированные коэффициенты (финансовые функции) приведения (дисконтирования) и наращения дискретной постоянной ренты.
Они определяются так:
= = ;	= =

4.6 Среднесрочные выплаты и их погашение

В банковской практике большинства стран среднесрочным счи­тается кредит, выданный на срок от 2 до 5 лет. Кредиты, выданные на срок свыше 5 лет, считаются долгосрочными. Данная града­ция является достаточно условной и справедлива при стабиль­ной экономике и малой инфляции. Расходы, связанные с погашением займа и выплатой процентов по нему, называются расходами по обслуживанию долга или амортизацией займа. Существуют различные способы пога­шения задолженности. Участники кредитной сделки оговари­вают их при заключении контракта. В соответствии с условиями контракта составляется план погашения задолженности. Одним из важнейших элементов плана является определение числа вы­плат в течение года - определение числа, так называемых, срочных уплат (выплат) и их размеры.

Срочные уплаты рассматриваются как средства, предназначен­ные для погашения как основного долга, так и текущих процент­ных платежей. При этом средства, направляемые на погашение (амортизацию) основного долга, могут быть равными или изме­няющимися по каким-либо законам, а плата за кредит, вычи­сленная по сложным процентам, будет выплачиваться отдельно. Иногда в течение ряда лет выплачиваются только проценты за кредит, а сам долг погашается в оставшееся время в рассрочку, т.е. несколькими платежами, или разовым платежом.

Погашение кредита может также производиться аннуитетными платежами, вносимыми через равные промежутки времени и содержащими как выплату основного долга, так и процентный платеж за пользование кредитом. Величина аннуитета может быть постоянной, а может изменяться в арифметической или геомет­рической прогрессии (как указывалось выше).

Величина срочных уплат зависит от величины кредита, его срока, наличия и продолжительности льготного периода, размера процентной ставки и ряда других. Однако, как правило, проценты за кредит предусматривается выплачивать и в льготном периоде..

Погашение долга равными срочными выплатами.

Условиями кредитного контракта может предусматриваться погашение долга равными срочными уплатами в конце каждого расчетного периода. Каждая срочная выплата (Y) будет являться суммой двух величин: годового расхода по погашению основного долга (R) и процентного платежа по займу (I): Y= R + I.

В этом случае остаток основного долга и суммы процентных платежей уменьшаются от периода к периоду, годовой расход погашенного основного долга растет, а срочные уплаты будут являться аннуитетами ренты постнумерандо. Величина кредита (CR) равна сумме всех дисконтированных аннуитентов и является современной величиной всех срочных уплат. Исходя из этого можно записать:

CR = 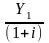+ + 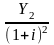+ 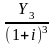… + 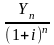, (ф. 4.1)

где Y₁ = Y₂ = Y₃ = … = Y_n – размеры срочной выплаты;

i – ставка процентов по займу.

Упростив данное выражение получим:

CR = Y∙ .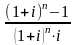

Из него можно определить величину срочной выплаты:

Y = CR ∙ 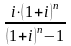, (ф. 4.2)

где - коэффициент погашения задолженности.

Далее составляется план погашения кредита по типу табл. 4.2, приведенной выше. Причем выплата будет подразделяться на составляющие погашения долга (R) и уплаты процентов (I). Погашение основного долга может производиться равными и неравными выплатами.

На практике часто представлены случаи, когда на этапе разработки контракта или в ходе его реализации, в силу внешних обстоятельств, приходится изменять условия выплаты ренты.

Это означает, что требуется изменение условий погашения кредита, которое называется конверсией рент (или займов).

Простейшим случаем конверсии является замена ренты разовым платежом (выкуп ренты) или, наоборот, замена разового платежа рентой (рассрочка платежа). К более сложному случаю относится объёдинение нескольких рент с разными характеристиками в одну – консолидация рент. Наиболее общий случай конверсии – замена ренты с одними условиями на ренты с другими условиями. Если предполагается, что конверсия не должна приводить к изменениям финансовых последствий для каждой из участвующих сторон, то конверсия должна основываться на принципе финансовой эквивалентности.

Конверсия рент широко применяется при реструктуризации задолженности. При этом достаточно часто условия погашения долга смягчаются при соблюдении главных составляющих принципа эквивалентности.

При любом методе конверсии первоначально определяются суммы выплаченного основного долга и величина непогашенной его части. Непогашенная часть долга рассматривается как новый долг, подлежащей уплате по новым условиям.

4.7 .Льготные кредиты

В условиях инновационного кредитования финансовая практика знает немало примеров, ког­да долгосрочные кредиты выдаются на льготных условиях. Это может быть вызвано социальными или какими-либо другими соображениями. Одной из наиболее существенных льгот явля­ется предоставление кредита по ставке, значительно ниже обще­принятой на данный момент. В результате предоставления по­добной льготы заемщик фактически получает субсидию. Кредитор же теряет определенную сумму в результате этой сделки. Эта доб­ровольно упущенная выгода кредитора, связанная с применени­ем более низкой процентной ставки, чем была принята на рынке капиталов, что называется грант-элементом, который может быть определён в виде абсолютной или относи­тельной величины.

Рассмотрим метод расчета абсолютного грант-элемента при предоставлении льготного кредита с условием его погашения равными срочными уплатами. Введем следующие обозначения:

CR _- сумма предоставленного кредита;

_{n -} срок кредита;

_{g -} льготная процентная ставка, по которой предоставлен кредит;

_{i -} общепринятая процентная ставка;

_{Y -} величина срочной выплаты при использовании общепринятой процентной ставки;

_{Y′ -} величина срочной уплаты по льготной ставке;

_{W -} величина абсолютного грант-элемента.

Для расчета грант-элемента воспользуемся формулами ф.4.1 и ф.4.2 и определим недополучение от нового кредита:

_{W = (Y - Y′) ∙} , (ф.4.3)

где _{Y =} CR∙ , а _{Y′ =} CR∙ .

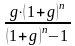Для расчета грант-элемента используется и другой метод. Так, абсолютный грант-элемент определяется как разность между номинальной суммой кредита и современной величиной пога­сительных платежей и выплаченных процентов:

_{W =} CR – G,

где G - современная величина срочных выплат, вносимых в счет погашения займа, определенная по общепринятым ре­альным ставкам i.

Относительный грант-элемент равен:

w = 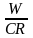= 1 - .

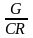При сохранении ранее принятых условий кредита (погаше­ние производится равными срочными уплатами в течение n лет по льготной ставке g в то время как на денежном рынке преоб­ладает процентная ставка i, причем i > g) срочная выплата в кон­це каждого года может рассматриваться как член постоянной ренты, а величина долга — как сумма ренты.

Все переменные приведенных формул определяются условиями выдачи и погашения займа. Выведем формулы для расчёта _{W и} w при условии, что долг и проценты выплачиваются в виде постоянных срочных уплат. Для проведения анализа выдачи льготных займов этого бывает достаточно.

В соответствии с установленными выше условиями срочная уплата составит: Y = 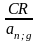, а современная величина всех платежей по займу должника составит Y∙ , откуда абсолютная величина грант-элемента определится так:

_{W = 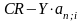= = 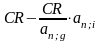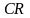∙ 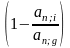,} (ф.4.4)

_{а относительный грант-элемент составит:}

w = 1 - 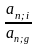, (ф.4.5)

где = ; 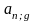= 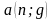- коэффициенты приведения постоянных годовых рент постнумерандо, определённых для процентных ставок i и g, причем i > g.

Предоставление льготного периода увеличивает выгодность кредита для заёмщика. Льготный период может предусматривать отсрочку всех платежей или выплату только процентов. Льготный период увеличивает грант-элемент. Если в льготном периоде должник выплачивает только проценты, то современная величина поступлений по долгу определится как сумма двух составляющих: современных величин процентных платежей в льготном периоде и срочных уплат в оставшемся периоде:

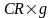
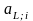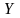
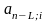
G = 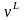 +   , (ф.4.6)

где 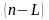- продолжительность реального периода погашения задолженности;

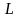- продолжительность льготного периода.

Относительный грант-элемент составит:

w = 1 - = 1 - ,

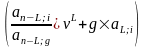где = 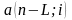; 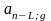= 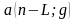; = 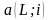- коэффициенты приведения постоянных рент со сроками и и ставками i и g;

- дисконтный множитель по ставке i.

4.8 Лизинг как форма финансирования инвестиционных проектов

Лизинг представляет собой долгосрочную аренду машин и оборудования на срок от 3 до 20 лет и более, купленных арен­додателем для арендатора с целью их производственного исполь­зования при сохранении права собственности на них за арендо­дателем на весь срок договора. В зависимости от срока, на который заключается договор арен­ды, различают три вида арендных операций:

краткосрочная аренда на срок до года - рейтинг;

среднесрочная аренда на срок от 1 года до 3 лет - хайринг;

долгосрочная аренда от 3 до 20 лет и более - лизинг.

Лизинг можно рассматривать как специфическую форму инвестирования в основные фонды, которая осуществляется посредством специальных (лизинговых) компаний кредитующих арендатора, путём приобретения для инвесто­ра машин и оборудования. Он появился в начале 1950-х годов в США, а с 1960-х го­дов - в странах Западной Европы. Его возникновение обуслов­лено потребностью в инвестициях в условиях научно-технического прогресса и невозможностью ее полного удовлетворения за счет традиционных методов финансирования - использования собственных и заемных средств. В рамках долгосрочной аренды различают два основных вида лизинга — финансовый и опера­ционный.

Финансовый лизинг - это соглашение, предусматривающее выплату в течение всего периода действия сумм, покрывающих полную стоимость амортизации оборудования или большую ее часть, а также прибыль арендодателя. По истечении срока дей­ствия такого соглашения арендатор может вернуть объект арен­ды арендодателю, заключить новое соглашение на аренду дан­ного оборудования, купить объект лизинга по остаточной сто­имости.

Операционный лизинг - это соглашение, срок которого коро­че амортизационного периода оборудования. После завершения срока действия соглашения предмет договора может быть воз­вращен владельцу или вновь сдан в аренду.

С экономической точки зрения лизинг имеет сходство с кре­дитом, предоставленным на покупку оборудования. При покупке реальных активов в кредит покупатель вносит в установленные сроки платежи в погашение долга; при этом продавец реальных активов для обеспечения возврата кредита сохраняет за собой право собственности на кредитуемый объект до полного пога­шения ссуды.

При осуществлении лизинговых операций весьма сложным вопросом является определение суммы лизинговых (арендных) платежей. При этом используются методически обоснованные расчеты, связанные со стоимостью объекта, передаваемого в арен­ду, а также продолжительностью лизингового контракта. В состав лизингового платежа входят следующие основные элементы:

• амортизация;

• плата за ресурсы, привлекаемые лизингодателем для осу­ществления сделки;

• лизинговая маржа, включающая доход лизингодателя за ока­зываемые им услуги (1—3%);

• рисковая премия, величина которой зависит от уровня раз­личных рисков лизингодателя.

Последние три элемента (плата за ресурсы, лизинговая мар­жа, рисковая премия) составляют лизинговый процент. Для расчета суммы арендных платежей воспользуемся фор­мулой, известной в финансовой математике как погашение долга равными срочными уплатами. Каждая срочная уплата (Y) будет являться суммой двух величин: суммы, идущей на погашение основного долга (R) и процентного платежа по нему (I): Y = R + I. В этом случае остаток основного долга и суммы процентных платежей уменьшаются от периода к периоду.

Годовой расход погашенного основного долга растет, а срочные уплаты будут являться аннуитетами ренты постнумерандо.

Если обозначить сумму арендных платежей как Y сумму амор­тизации или стоимость арендуемого имущества – ОС, срок кон­тракта - n, лизинговый процент – j, периодичность арендных платежей в году – m, то формулу для расчета суммы арендных платежей можно записать следующим образом:

а) при разовом взносе платежей в течение года:

Y = ОС ∙ 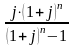; (ф.4.7)

б) при взносе платежей m раз в течение года:

Y = ОС ∙ 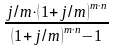; (ф.4.7)

Обратимся к примеру. Стоимость арендного оборудования - грузовых вагонов составляет 150 млн. рублей, срок лизингового договора – 3 года, лизинговый процент составляет 9% годовых, взнос платежей производится два раза в год. Тогда, величина лизинговых платежей будет постоянная и составит:

Y = 150,0 ∙ 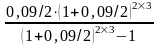= 150,0 ∙ 0,1939 =

= 29,085 млн. рублей

При заключении лизингового соглашения обычно не пре­дусматривается полная амортизация стоимости арендованного оборудования. Как правило, ликвидационная (остаточная) сто­имость оборудования засчитывается в пределах 10% первоначаль­ной стоимости. В этом случае сумму лизингового платежа кор­ректируют на процент остаточной стоимости, величину которого согласовывают между собой арендатор и арендодатель. Для это­го используется формула корректировочного множителя

K = 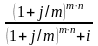, где i - процент остаточной стоимости.

За счет остаточной стоимости размер лицензионного платежа, скорректированный данным коэффициентом, несколько снизится.

Гносеологические термины и понятия

Амортизация кредита	Непрерывные ставки наращения
Английская практика	Операционный лизинг
Аннуитет	Переводной вексель или тратта
Банковский кредит	Период ренты
Векселедержатель	План погашения кредита
Виды ставок (процентные и учетные)	Потребительский кредит
Выкуп ренты	Проценты декурсивные
Германская практика	Процент остаточной стоимости
Годовая номинальная учетная ставка	Простая процентная ставка
Грант-элемент (абсолютный)	Простая учетная ставка
Грант-элемент (относительный)	Проценты антисипативные
Договор аренды	Процентная ставка – сила роста
Долгосрочные кредиты	Рассрочка платежа
Дисконтирование	Реальный период кредитования
Дисконтирование по сложным ставкам	Рейтинг
Дисконтный множитель	Реструктуризация задолженности
Дискретные ставки наращения	Рисковая премия
Дисконтирование по сложным ставкам	Сложная процентная ставка
Залоговые операции	Сложная учетная ставка
Затраты банка по обслуживанию долга	Срок ренты
Инвестиционный кредит	Срочные ренты
Коммерческий кредит	Срочные уплаты (выплаты)
Консолидация рент	Среднесрочные кредиты
Конверсия рент (или займов)	Точные проценты
Корректировочный множитель	Французская практика
Лизинг	Финансовая рента
Лизинговая маржа	Финансовый лизинг
Ломбардный кредит	Форфейтинг
Льготные кредиты	Хайринг
Льготный период	Эквивалентность ставок
Множители наращения	Эффективная учетная ставка
Наращенная величина
Годовая номинальная процентная ставка
Обыкновенные проценты с точным числом дней
Обыкновенные проценты с приближённым числом дней
Погашение кредита изменяющимися частями
Погашение кредита равными частями
Современная (приведенная) величина
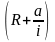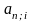
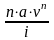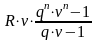
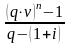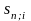
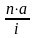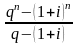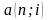
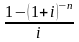