При выдаче ссуды на п лет из условия т погасительных пла­тежей в году последовательные номера месяцев за весь период погашения могут быть записаны в обратном порядке следующим образом:

t₁ = n∙m; t₂ = m∙n – 1; t₃ = m∙n – 2; … t_n = 1.

Сумма этих чисел (q) по формуле арифметической прогрессии будет равна:

Q = = = .

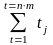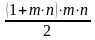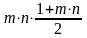В каждом платеже доля порядкового числа данного месяца составит . Абсолютная величина процентного платежа в каж­дом платежном периоде будет равна: 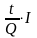; (при I = P ∙ n ∙ t), где I - сумма всех процентных платежей; P - первоначальная сумма долга; i - процентная ставка, выраженная десятичной дробью. Сумма погашенного долга (U_k) на конец периода К (или момент k) равна:

U_k = Y_k - ,

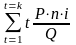где Y_k - оставшаяся часть непогашенного долга на момент k.

Воспользуемся спосо­бом, когда процентный платеж рассчитывается методом начислений с уменьшением остатка долга. При этом процентный платеж за пользование потребитель­ским кредитом начисляется предварительно: для первого меся­ца (периода) процентный платеж рассчитывается на всю вели­чину долга, а в каждый следующий месяц — на оставшуюся часть долга, т.е. на величину долга, уменьшенную на уже выплачен­ную часть, а сам же долг выплачивается равными долями. Предположим, что величина кредита равна Р и он должен выплачиваться равными месячными платежами т раз с начис­лением процентов по годовой ставке i.

Тогда процентный платёж для первого месяца составит:

I₁ = ;

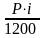во втором месяце он составит:

I₂ = = ;

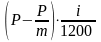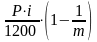в третьем месяце он составит:

I₃ = = ;

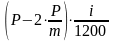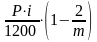в месяце m он составит:

I_m = = = ;

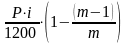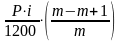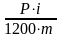Для определения общей величины процентных выплат за предоставленный кредит просуммируем их месячные значения и обобщив их получим:

I = 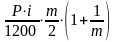= 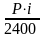∙ 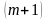, где 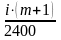- процентный коэффициент.

При ежемесячной выплате кредита равными долями её величина будет равна: q = .

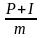Рассмотрим пример. Предприятие купило в кредит автомобиль стоимостью 452,0 тыс. рублей (Р = 451,2 тыс. руб.) под 18% (i = 18) годовых. Погашение задолженности производится ежемесячными платежами в течение года (m = 12). Составим план погашения (амортизации кредита) с уменьшением остатка долга.

Ежемесячная выплата основного долга:

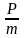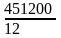= = 37600 руб.

План погашения кредита показан в табл.4.2.

Ежемесячные процентные платежи будут уменьшаться. Общая сумма процентных платежей составит:

I = ∙ = 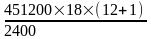= 43992 руб.

Средняя величина ежемесячных взносов составит:

q = 41266 руб.

Таблица 4.2.

План погашения кредита

Месяц	Непогашенная сумма основного долга, тыс. руб.	Процентный платёж		Месяч-ная оплата долга, тыс. руб.		Сумма месячно-го погаше-ния, тыс. руб.
		доля	тыс. руб.
0	451200	0,91667	х		х		х
1	413600	0,83333	6768		37600		44368
2	376000	0,75000	6204		37600		43804
3	338400	0,66667	5640		37600		43240
4	300800	0,58333	5076		37600		42676
5	263200	0,50000	4512		37600		42112
6	225600	0,41667	3948		37600		41548
7	188000	0,33333	3384		37600		40984
8	150400	0,25000	2820		37600		40420
9	112800	0,16667	2256		37600		39856
10	75200	0,08333	1692		37600		39292
11	37600	0,00000	1128		37600		38728
12	0	0,91667	564		37600		38164
Итого:			43992		451200		495192

4.4 Инвестиционный кредит и дисконтирование

Инвестиционный кредит в условиях рынка выступает в различных формах. Основными являются коммерческий и банковский кредит.

Коммерческий кредит есть предоставление инвестиционных услуг одним субъектом сделки другому с оплатой через определенное время, т.е. происходит отсрочка уплаты денег за инвестиционные услуги. Распространенным инструментом этого кредита является коммерческий вексель.

Вексель — это особый вид пись­менного долгового обязательства, дающий его владельцу бесспор­ное право требовать по истечении указанного в нем срока упла­ты денег с должника. Векселя могут быть простыми и переводными. Простой век­сель представляет собой долговое обязательство, выдаваемое за­емщиком на имя кредитора, и содержит указание места и вре­мени выдачи долгового обязательства, его суммы, места и вре­мени платежа и наименование лица, которому заемщик обязан произвести платеж.

Переводной вексель, или тратта, представляет собой письмен­ный приказ одного лица (кредитора) другому лицу (заемщику) об уплате суммы, обозначенной в векселе, третьему лицу.

Банковский кредит — это кредит, предоставляемый одним субъектом сделки другому в виде денежной ссуды. Механизм оформления банковских ссуд предусматривает различные вари­анты, в том числе выписку ссудозаемщиком векселей на имя кредитора.

Векселедержатель (кредитор) или владелец иных долговых обязательств в случае необходимости получения денег по век­селю или другим долговым обязательствам ранее указанных в них сроков может продать его банку или другому субъекту по по­ниженной цене, т.е. по цене ниже номинальной стоимости век­селя, указанной в нем. Такая сделка носит название учета век­селя, или дисконтирования. Сумма, полученная владельцем век­селя в результате этой сделки, называется дисконтированной величиной. Она ниже номинальной стоимости векселя на ве­личину процентного платежа, вычисленного со дня дисконти­рования до дня, ранее предусмотренного для погашения век­селя. Дисконтом называется разность между номинальной стоимо­стью долгового обязательства и суммой, полученной векселедер­жателем в результате учета векселя.

Дисконтирование векселя является, по существу, формой кредитования векселедержателя путем досрочной выплаты ему обозначенной в векселе суммы за вычетом определенных про­центов. Для субъекта сделки, принявшего к учету вексель, дис­конт является доходом. Дисконт рассчитывается на основе так называемой учетной ставки, величина которой зависит от сро­ка, остающегося до оплаты обязательства, и существующих бан­ковских процентных ставок. Учетные ставки также рассчитыва­ются в процентах.

Термин «дисконтирование» употребляется в финансовом ме­неджменте весьма широко. Под этим термином может пониматься способ нахождения величины P на некоторый момент времени при условии, что в будущем при начислении на нее процентов она могла бы составить наращенную сумму S.

Величину P, най­денную дисконтированием наращенной величины S, называют текущей современной, или приведенной, величиной. С помощью дисконтирования в финансовых вычислениях учитывается фактор времени.

Например, если сегодня инвестируется 10,0 млн. руб., рас­считывая получить 10% дохода, то через год стоимость ваших инвестиций составит 11,0 млн. руб. — это будущая стоимость ва­шей инвестиции, а текущая стоимость составляет 10,0 млн. руб.

При математическом дисконтировании решается задача, об­ратная определению наращенной суммы. Сформулируем ее сле­дующим образом: какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процентов по ставке i получить наращенную сумму, равную S?

Для отражения этой задачи используем формулу наращения по простой ставке процентов получим:

P = S ∙ ,

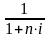где - дисконтный множитель, показывающий, во сколько раз первоначальная сумма ссуды меньше наращенной. Преобразуем данное выражение, получим:

D = S – P = P ∙n ∙i.

Эта разность называется дисконтом. Его следует отличать от дивизора ( множителя D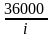^* = ), в отличие от которого он характеризует фактический натуральный стоимостной прирост.

Математический метод дисконтирования может применять­ся с использованием не только простой, но и сложных ставок.

Для этого из выражения S = P (1+ i)ⁿ найдем значение P для сложной процентной ставки:

P = S ∙ 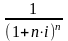= S ∙ (1+ i)^-n,

где = (1+ i)^-n – дисконтный (учётный) множитель. Значения этого множителя обычно представляются в табулированном виде в специальных справочниках по финансовым вычислениям.

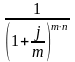При начислении процентов т раз в году получим следующее выражение: P = S ∙ = S ∙ 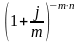, где = - дисконтный множитель.

Как указывалось выше, разность S – P = D является дисконтом, поэтому можно записать:

D = S – S ∙ = S .

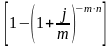Приведенная величина P представляет приведенную величину (современную – present value - по англ.). Одним из её свойств является то, что величина процентной ставки, по которой производится дисконтирование, и её современная (приведенная) величина находятся в обратной зависимости, иначе, чем выше процентная ставка, тем меньше современная величина при прочих равных условиях. В такой же обратной зависимости находятся современная величина и срок платежа. С увеличением срока платежа n современная величина будет уменьшаться.

В учетных (дисконтных) операциях, помимо сложной процентной ставки, широко применяется слож­ная учетная ставка. В этом случае дисконтирование осуществляется по формуле:

P = S ∙ (1 - с)ⁿ,

где с – сложная годовая учетная ставка. Дисконт в этом случае определится как разность:

D = S – P = S – S ∙ (1 - с)ⁿ = S ∙ [ 1 – (1 - с)ⁿ].

Зная величины S, P и n можно определить значение сложной учетной ставки (с):

S = 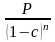, откуда с = 1 - .

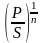Различие в величине дисконтных множителей при использовании простой (d) и сложной (с) учётных ставок, равных по своей величине, будет зависеть от срока ссуды. При дисконтировании m раз в году используется номинальная учетная ставка.

Расчёт дисконтированной величины при номинальной учетной ставке производится по формуле:

Р = S ∙ ,

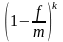где f – номинальная учетная ставка;

а k = m∙n – общее число периодов дисконтирования.

При дисконтировании m раз в году вводится понятие эффективной ставки, под которой имеется ввиду сложная годовая учётная ставка, эквивалентная номинальной учётной ставке при заданном значении m.

Эффективная процентная ставка – ставка, отражающая реальный доход от коммерческой сделки, иначе, ставка, по которой фактически были начислены проценты на первоначальную сумму.

Из приведенных выше определений эффективной ставки можно записать:

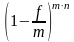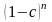= или = ,

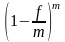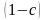тогда c = 1 - .

Отсюда можно сделать вывод, что эффективная учётная ставка (c) меньше номинальной учётной ставки (f).

Величина номинальной учетной ставки f при дисконтировании m раз в году определится так:

f = .

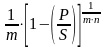Сроки ссуды при дисконтированной сложной годовой ставке и номинальной учетной ставке m раз в году составят:

при сложной годовой ставке	при номинальной учётной ставке
n = ;	n = .

Для расчета наращенных сумм и дисконтирования были использованы различные виды ставок q, i, j, f, c, d. Использование в финансовой сделке различных видов ставок, при равных условиях, приводит к различным финансовым результатам. Так как результаты финансовых сделок зависят от числа перио­дов начисления процентов.

При равенстве ставок q = i = j = f = c = d множители наращения будут представлять сле­дующий мажорантный ряд:

при n < 1	(1 + i)n	<	(1 + n∙q)	<	(1 - n∙c)-1	<	(1 - c)-n
при n > 1	(1 + n∙q)	<	(1 + i)n	<	(1 - c)-n	<	(1 - n∙d)
при n = 1	(1 + n∙q)	=	(1 + i)n	<	(1 - n∙d)	=	(1 - c)n
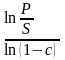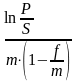