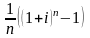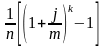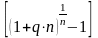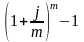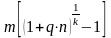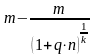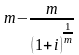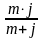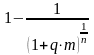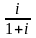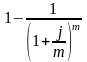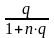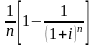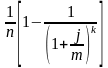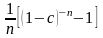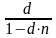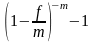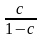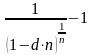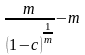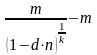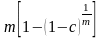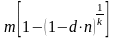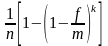Вопросы для самопроверки

1.	Какие основные факторы влияют на развитие современного рынка венчурной индустрии в России и за рубежом?
2.	Какие несоответствия представления венчурных проектов на рынке?
3.	В каком состоянии сейчас находится Российская венчурная индустрия?
4.	Что предусматривает договор о совместных научных исследованиях и разработках в США?
5.	В чем заключается «Идея CRADA» ?
6.	Сколько на сегодняшний день принято рамочных программ ЕС?
7.	Чему посвящались рамочные программы?
8.	Что представляет Седьмая рамочная программа, какова её структура?
9.	В чем ЕС видит мировое лидерство в области ИКТ ?
10.	Как ЕС взаимодействует с Россией по НИОКР ?
11.	В какой венчурной продукции Индия имеет определенное лидерство в экспорте?
12.	Как изменился облик Китая в начале 21 века?
13.	В рамках каких государственных программ ведется совершенствование научно-технического комплекса Китая?
14.	Чем привлекает Китай Транснациональные компании (ТНК)?
15.	Какие составляющие инновационной технологический инфраструктуры получили распространение в России?
16.	Цели и задачи технопарков России в сфере высоких технологий?
17.	Что такое особые экономические зоны в России?

Раздел 4. Финансовые основы инвестирования

4.1.	Сущность процентных, учётных и других видов ставок и платежей
4.2.	Расчеты по залоговым операциям
4.3.	Потребительский кредит
4.4.	Дисконтирование и его сущность
4.5.	Финансовые ренты и потоки
4.6.	Среднесрочные и долгосрочные кредиты и их погашение
4.7	Льготные кредиты
4.8	Лизинг как форма финансирования инвестиционных проектов
	Гносеологические термины и понятия
	Вопросы для самопроверки

4.1. Сущность процентных, учетных и других видов ставок и платежей

В развивающейся рыночной экономике (а по аналогии и для других случаев развития экономики) денежный капитал имеет механизмы собственного воспроизводства, противодействуя его возможному обесценению в результате негативных факторов её развития (темпам инфляции, рискам и др.). «Механизм процента» обеспечивает доходность капитала от кредитной сделки для кредитора и текущую его стоимость для заёмщика. Процентная ставка показывает, какая доля суммы выданного в заём капитала будет возвращена владельцу в виде полученного дохода. Размер процентной ставки определяется рядом обстоятельств: темпом инфляции (расширением потребительского интереса, приводящего к снижению текущей стоимости товаров и услуг), рисками займа, сроком возврата средств, механизмами возврата.

В зависимости от последовательности операций ставки раз­личаются на:

процентные при следующей схеме оборота: деньги → возврат денег + процент;

учетные при схеме оборота: процент → деньги → возврат денег.

Если предприятие сначала берет кредит в банке, а потом вы­плачивает полученную сумму с процентными начислениями, то речь идет о процентной ставке. Если же предприятие вы­пустило собственный беспроцентный простой вексель и получило под него денежную сумму, которая меньше но­минальной суммы векселя, а затем погашает всю вексельную сумму, то речь идет об учетной ставке.

Процентные и учетные ставки различаются также по способам начисления процентов. При этом выделяют два подхода: от настоящего к будущему и от будущего к настоящему. Первый подход характеризуется ставками наращения (interest base rate), а второй дисконтными или учетными ставками (discount base rate). Проценты, полученные по ставке наращения, называют декурсивными, а по учетной ставке – антисипативными. Остановимся на разновидности процентных и учетных ставок:

• Простые (процентная – q и учетная - d) ставки - в них проценты начисляются на первоначально вложенную сумму денег. Начисленные проценты при следующем расчете не учитываются.

• Сложные (процентная – i и учетная - c) ставки, когда проценты начисляются на проценты. При этом при европейском методе расчета проценты начисляются 1 раз в год.

• Годовые номинальные (процентная – j и учетная - f) ставки, когда проценты начисляют­ся несколько раз в год (nominal annual rate method) - американский метод.

Соотношения между различными процентными и учетными ставками приведено в табл. 4.1.

Важное место в системе процентных ставок занимает ставка рефинансирования Центрального Банка России, по которой им выдаётся кредит коммерческим банкам, а также она используется при начислении процентов в налоговой системе при несвоевременном погашением пени и штрафов.

Таблица 4.1 (начало).

Соотношения между различными

процентными и учетными ставками

Обозначение	Формулы взаимосвязи ставок (начало)
	q	i	j
2	3	4	5
q	Простая процентная ставка
i		Сложная процентная ставка
j			Годовая номинальная процентная ставка
f
c
d
n – число годовых периодов начислений;
m – число месячных периодов начислений;
k =n∙m – общее количество периодов начислений.

q - Простая процентная ставка

i - Сложная процентная ставка

j - Годовая номинальная процентная ставка

f - Годовая номинальная учетная ставка

с - Сложная учетная ставка

d - Простая учетная ставка

Процентные и учетные ставки решают одинаковые задачи: устанавливают: доходность при операции наращения и размеры дисконтированных сумм при учетных операциях. Возможен выбор таких процентных или учетных ставок, при использовании которых финансовые последствия будут равноценными. Ставки, обеспечивающие равноценность финансовых послед­ствий, называются эквивалентными или релятивными (относи­тельными). Эквивалентность определяется для двух вари­антов: когда временные базы (К – число дней в году) равны и когда они различны. Для каждого периода наращения рассчитывается своя эквивалентная ставка.

Таблица 4.1 (окончание).

Соотношения между различными

процентными и учетными ставками

Таблица 4.1 (окончание).

Соотношения между различными

процентными и учетными ставками

Обозначение	Формулы взаимосвязи ставок (окончание)
	f	c	d
2	3	4	5
q
i
j
f	Годовая номинальная учетная ставка
c		Сложная учетная ставка
d			Простая учетная ставка
n – срок ссуды или кредита в годах;
m – число платежей в течении года;
k =n∙m – общее количество периодов начислений.

Различают три метода процентных расчётов, которые зависят от выбранного периода начисления.

1. Точные проценты с точным числом дней ссуды («англий­ская практика»). При этом методе определяется фактическое число дней (t) между двумя датами (датой получения и погашения креди­та), продолжительность года принимается равной К= 365 (366) дней.

2. Обыкновенные проценты с точным числом дней ссуды («фран­цузская практика»); величина t рассчитывается, как и в преды­дущем случае.

3. Обыкновенные проценты с приближенным числом дней ссуды («германская практика»); величина t определяется коли­чеством месяцев по 30 дней в каждом начиная с момента выда­чи ссуды и до момента ее погашения и точным числом дней ссуды в неполном месяце; продолжительность года К= 360 дней.

При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.

Замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет финансовых отношений сторон в рамках одной операции. Для участвующих в сделках сторон обычно безразлично, какой вид ставки представлен в контракте. Формулы эквивалентности ставок, представленные в табл. 4.1, получены из равенства попарно взятых множителей наращения.

При обосновании и выборе инвестиционных решений большое значение имеет непрерывное наращение. С помощью непрерывных процентов можно учесть сложные закономерности процесса наращения, например, использовать изменяющиеся по определённому закону процентные ставки.

При непрерывном наращении процентов применяют особый вид процентной ставки – силу роста (force of interest). Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени. Можно также установить эквивалентность дисконтного множителя и силы роста непрерывных процентов, что выражается следующей формулой:

= = .

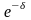Аналогично для простой и сложной учетных ставок может быть установлена эквивалентность силы роста и учетных ставок.

Таким образом, дискретные и непрерывные ставки наращения находятся в функциональной зависимости друг от друга. Основной проблемой выбора ставки среди возможных вариантов финансирования является критерий отбора, который устанавливается из условий самого инвестиционного проекта.

4.2 Расчёты по залоговым операциям

Залоговые операции представляют собой краткосрочный кредит под залог легкореализуемого движимого имущества. Одной из форм залоговых операций является ломбардный кредит. Такой кре­дит может осуществляться и в форме банковского кредита под залог де­понируемых в банке ценных бумаг. В этом случае в залог принимаются ценные бумаги, котирующиеся на фондовой бирже или имеющие органи­зованный свободный рынок. Сумма кредита составляет от 50 до 90% их курсовой стоимости. Срок кредита, как правило, не пре­вышает трех месяцев.

Контракт на получение ломбардного кредита может преду­сматривать различные условия выплаты долга. Так, заемщик может:

• погасить весь долг единовременным платежом в срок, пре­дусмотренный контрактом;

• выплатить в срок лишь часть долга, а оставшуюся часть погашать в следующем перио­де;

• продлить срок погашения на следующие три месяца.

При расчетах учитывается точное количество дней в месяце, а про­должительность года принимается равной 360 дням.

В случае если заемщик не погасит кредит вовремя, он обязан рассчитаться с кредитором по увеличенной (штрафной) процент­ной ставке за весь период просрочки платежа. Если кредит все же не будет погашен, право собственности переходит к креди­тору, который реализует имущество и удерживает из выручки сумму долга вместе с начисленными процентами.

Рассмотрим пример расчета при использовании ломбард­ного кредита.

Банк предоставил клиенту (предприятию) кредит на 3 месяца с 15.05 по 15.08 под залог 200 акций, курсовая стоимость которых в день выдачи кредита (15.05) составляла по 25 тыс. руб. за акцию. Сумма кредита оценена в 60% курсовой стоимости залога. Кредит выдается под 12,5% (i = 12,5) годовых.

За обслуживание долга банк взимает 1,0% от номи­нальной суммы кредита.

Определим фактический размер кредита, полученного клиентом банка.

Курсовая стоимость залога: 200 ∙ 25 тыс. руб. = 5000 тыс. руб. (5,0 млн. рублей). Номинальная величина кредита: P = 5,0 ∙ 0,60 = 3,0 млн. руб.

Сумма процентных платежей за кредит (с 15.05 по 15.08, где t = 92 дня):

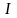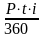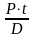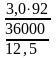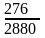= = = = = 0,0958 млн. рублей.

Затраты банка по обслуживанию долга составляли: 3,0∙0,01= 0,03 млн. рублей (30 тыс. рублей). Сумма кредита, полученная клиентом составляла:

3,0 – (0,0958 + 0,03) = 2,874 млн. рублей.

4.3 Потребительский кредит

Потребительский кредит предоставляется банка­ми, финансовыми компаниями или торговыми фирмами для приобретения потребительских товаров. Существуют различ­ные формы потребительского кредита, отличающиеся друг от друга методами и сроками его погашения. Так, например, по­требительский кредит может быть предоставлен с отсрочкой платежа и последующим разовым погашением всей суммы. Другой метод предусматривает погашение платежа в рассрочку — частями. Здесь проценты начисляются на всю сумму кредита, а сумма задолженности (сумма, предоставленная в кредит, плюс начис­ленные проценты) равномерно погашается на протяжении все­го срока кредита.

Разновидностью погашения потребительского кредита в рас­срочку является метод, при котором суммы процентных плате­жей и суммы погашения основного долга изменяются от периода к периоду, по мере изменения сроков погашения ссуды. При этом решается задача определения срока задолженности на лю­бой момент срока погашения кредита. Наиболее распространены методы погашения потребительского кредита равными частями и изменяющимися суммами. Остановимся на них подробнее.

Погашение потребительского кредита равными частями. При погашении потребительского кредита равными частями наращенная сумма долга (S) определяется по уже известной формуле:

S = P (1 + n∙i),

а сумма разового погашающего платежа будет зависеть от числа погашающих платежей в году (m). Тогда сумма разового погасительного платежа равна:

q =

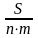
где q - сумма погасительного платежа; n - срок кредита в годах; m - число погасительных платежей в году. Так как проценты начисляются на всю сумму первоначаль­ного долга в течение всего срока погашения, то, несмотря на уменьшение величины долга с каждым платежом, фактическая процентная ставка оказывается значительно выше ставки, пре­дусмотренной при заключении сделки.

Погашение потребительского кредита изменяющимися суммами. При погашении кредита изменяющимися суммами решаются две задачи: определения суммы, идущей на погашение основного долга, и суммы процентных платежей.

Для решения этого вопроса можно воспользоваться «прави­лом 78». Название этого правила вызвано тем, что сумма поряд­ковых номеров месяцев года равна 78 (1 + 2 + 3 + ... + 12 = 78). В соответствии с этим правилом уплата процентов при первом платеже составит общей начисленной суммы процентов, а ос­тавшаяся часть платежа пойдет на уплату основного долга. При втором платеже на оплату процентов пойдет общей начи­сленной суммы процентов и т.д. Иначе говоря, процентные платежи являются убывающей арифметической прогрессией, сумма членов которой определя­ется по формуле:

S_n = или S_n = ,

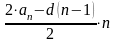где а₁ - первый член прогрессии;

а_п - последний член;

n - число членов;

d - разность членов прогрессии.