1)Определение производной. Задача нахождения скорости процессов привела к введению в математику понятия производной функции.

Пусть дана функция f(x), определенная на некотором интервале ]a, b[ и непрерывная на нем. Дадим аргументу приращение х, тогда функция получит приращениеf:

Отношение

является функцией от х и выражает среднюю скорость изменения функции f(x) относительно аргумента х на интервале х, х+х.

Предел отношения f/x приращения функции f к приращению аргумента х, когда х стремится к нулю, при условии, что этот предел существует, называется производ ной функции f(x) в точке .Таким образом, можно сделать следующий вывод: производная функции y = f(x):

В этом и состоит физический (в том числе механический) смысл производной.

По уравнению непрерывной линии у = f(x) найдем угловой коэффициент касатель ной к ней в данной точке М(х;f(x)), предполагая, что касательная существует. Функция y = f(x) в прямоугольной системе координат изображается кривой (рис.2). Возьмем на кривой точку М(х; f(x)) и Дадим аргументу х приращение х. По значению аргумента х+х получаем новое значение функции f(x+x), соответствующее точке М(х +х; f(х + х)) на кривой. Проведем секущую ММ и обозначим угол наклона секущей к оси Ох через . Из рисунка следует, что f/x=tg. При х  0 точка М перемещается вдоль кривой, приближаясь к точке М. Секущая ММ поворачивается вокруг точки М, и величина угла  изменяется. При приближении секущей ММ к к касательной МТ угол  приближается к углу  и

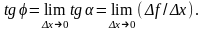
Угловой коэффи циент касательной

Итак, угловой коэффициент касател ьной к графику функции в данной точке равен значению ее производной в точке касания. В этом и состоит геометричес кий смысл производной.

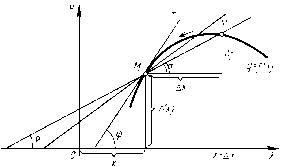
Описание скорости протекания биологических процес сов с помощью производной. Градиенты

Градиент (от лат. gradiens, род. падеж gradientis—шагающий) —характеристика, показывающая направ ление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».

В математике, градиент функции f это вектор, который указывает направление наискорейшего роста этой функции, и чей модуль равен скорости ее изменения в этом направлении.

Производные выс ших порядков. Частные производ ные. Производные второго и высших порядков. Производную f(x) функции у=f(x) будем называть производной пер вого порядка или просто первой производной этой функции. Производ ная функции f(x) является функцией от х, её можно дифференцировать .

Производная от производной назы вается производной второго порядка или просто второй производной.

Вторая производная обозначается сим волами: 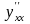(читается «игрек два штриха по икс»), («эф два штриха от икс»), d²y/dx² («дэ два игрек по дэ икс дважды), d²f/dx² («дэ два эф по дэ икс дважды»).

Исходя из Опре деления второй производной, можно записать:

Вторая производная в свою очередь есть функция от х, и её

можно дифферен цировать. Производ ная второй произ водной называется производной треть его порядка или третьей производ ной и обозначается

Производная (n – 1)-й производной (n – натуральное число) называется производ ной n-го порядка или n-й производной и обозначается

Например, для функции f(x) = x⁵ можно найти

Частные производные первого порядка. Частной производной первого порядка функции z = f(x,y) по аргументу х в рассматриваемой точке (х; у) называется предел

если он существует.

Частная производная функции z = f(x, y) по аргументу х обозначается одним из следующих символов: Аналогично частная производная по у обозначается и определяется формулой:

Так как частная производная – это обычная производная функции одного аргумента, то ее нетрудно вычислить. Для этого нужно пользоваться всеми рассмотренными до сих пор правилами дифференцирования, учитывая в каждом случае, какой из аргументов принимается за «постоянное число», а какой служит «переменной дифференцирования».Замечание. Для нахождения частной

производной, напри мер по аргументу х – df/dx, достаточно найти обыкновенную производную

функции f(x,y), считая последнюю функцией одного аргумента х, а у – постоянной; для нахождения df/dy – наоборот. Пример. Найти значения частных производных от функции f(x,y) = 2x²+ y² в точке Р(1;2).

Решение. Считая f(x,y) функцией одного аргумента х и пользуясь правилами дифференцирования, находим

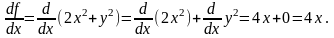
В точке Р(1;2) значение производной

Считая f(x;y) функцией одного аргумента у, находим

В точке Р(1;2) значение производной