5.8 Структурная устойчивость системы.

Понятие об области устойчивости и ее границах.

Устойчивость линейных стационарных САУ зависит не только от значений параметров системы, но и от ее структуры. В связи с этим различают структурно устойчивые и структурно неустойчивые системы.

Система, устойчивость которой может быть обеспечена выбором ее параметров без изменения структуры, называется структурно устойчивой.

Система называется структурно неустойчивой, если невозможно обеспечить ее устойчивость не при каких значениях параметров. Структурно неустойчивую систему можно сделать устойчивой только путем изменения ее структуры. При проектировании системы это можно обеспечить, например, включением в управляющее устройство тех или иных корректирующих устройств.

Следовательно, структурно устойчивые системы, в отличие от структурно неустойчивых, имеют в пространстве некоторых своих параметров область их изменения, в которой система остается устойчивой. Эту область называют областью устойчивости. При исследовании и проектировании систем чаще всего возникает задача определения влияния одного или двух ее параметров на устойчивость, т.е. задача выделения области устойчивости на плоскости одного или двух параметров системы. Прежде чем приступить к решению этой задачи необходимо знать, имеет ли данная система область устойчивости или нет, т.е. является ли данная система структурно устойчивости или структурно неустойчивой.

Для построения границ области устойчивости можно использовать различные критерии устойчивости. Однако, чаще всего используется критерий Гурвица. При этом границы области устойчивости строится, исходя из условия:

∆_n = a₀ ∆_n-1 = 0

обычно области устойчивости изображаются графически на плоскости двух параметров. Например, при исследовании системы управления ракет, вы встретитесь с областью устойчивости каналов автомата стабилизации на плоскости постоянных времени дифференцирующего контура.

Лекция 6

АНАЛИЗ КАЧЕСТВА ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ

СТАЦИОНАРНЫХ СИСТЕМ ПРИ ДЕТЕРМИНИРОВАННЫХ

ВОЗДЕЙСТВИЯХ. МОДЕЛИРОВАНИЕ СИСТЕМ

6.1 Показатели качества процесса управления и требования к ним

требование устойчивости линейной стационарной системы означает, что переходная составляющая процесса управления должна затухать. Однако это требование является далеко не достаточным условием ее практической пригодности. Требуется еще, во-первых, чтобы управляемая величина в установившемся режиме была достаточно близка к заданному значению, во-вторых, чтобы затухание переходного процесса было достаточно быстрым, а отклонения (колебания) управляемой величины в переходном процессе были невелики. поэтому при проектировании системы решается не только задача обеспечения ее устойчивости, но и задача обеспечения требуемого (заданного) качества процесса управления, в понятие которого входят точность работы системы в установившихся режимах и качество переходного процесса.

Величины, характеризующие поведение системы в установившемся и переходном процессах при определенном виде внешнего воздействия, принято называть показателями качества процесса управления (показателями качества системы).

В подавляющем большинстве практических задач исследование качества системы производится при детерминированных воздействиях.

Основным показателем качества работы системы в установившемся режиме является точность, оцениваемая величиной установившейся ошибки при различных типовых внешних воздействиях. Эту ошибку, в отличие от инструментальной (приборной), называют методической (структурной) ошибкой. Ее можно определить с помощью теоремы о конечном значении и коэффициентов ошибок.

К основным показателям качества переходного процесса относятся время регулирования, перерегулирование, число и частота колебаний управляемой (регулируемой) величины. Эти показателя часто определяются из графика переходной функции по задающему воздействию (см. рис. 6.1).

Рисунок 6.1

Время регулирования t_р. Под временем регулирования понимается время t_р, за которое переходный процесс практически заканчивается. Момент окончания переходного процесса определяется по уменьшению абсолютного значения разности | h(t) – h_y | до допустимо малой величины ∆. Величину ∆ обычно принимают равной 0,05h_y. Время регулирования определяет длительность переходного процесса, т.е. ее быстродействие. Чем меньше t_р, тем быстрее наступает установившийся режим.

Перерегулирование σ. Перерегулированием σ называется максимальное отклонение управляемой величины от установившегося значения, выраженное в процентах:

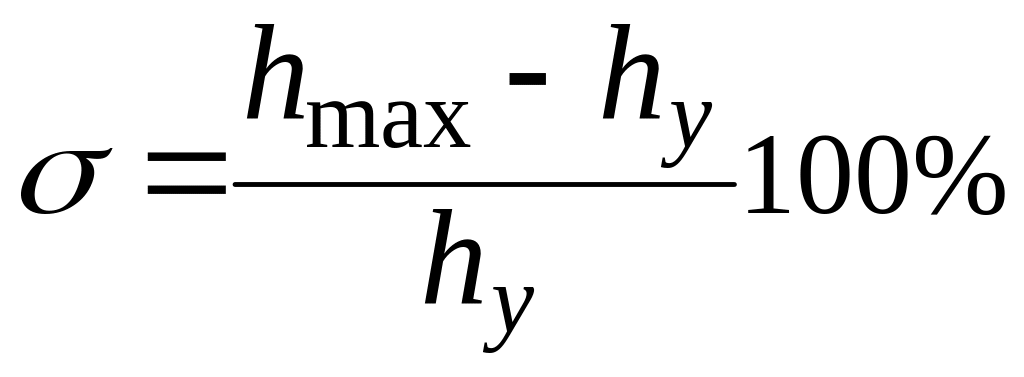
Перерегулирование в системах не должно быть слишком большим. При большой величине σ возможны значительные динамические ошибки и динамические усилия в механических частях систем или чрезмерные перенапряжения в электрических элементах. Для многих САУ условия работы требуют, чтобы величина перерегулирования не превышала 10-30 %. В некоторых случаях требуется, чтобы переходный процесс протекал вообще без перерегулирования, т.е. был монотонным; в ряде случаев может допускаться перерегулирование 50-70 %.

Число колебаний N_h. Под числом колебаний N_h понимается количество колебаний управляемой величины за время переходного процесса около ее установившегося значения. Число колебаний характеризует колебательность системы. Если N_h > 1, то переходный процесс называют колебательным. Малоколебательные переходные процессы характеризуются наличием N_h ≤ 1. системы, обладающие колебательными и малоколебательными переходными процессами, называют системами с перерегулированием.

Обычно приемлемым числом колебаний в САУ считается 1-2. однако, бывают системы, в которых колебательность не допускается совсем. С другой стороны, в ряде систем иногда допускается три и более.

Частота колебаний f_h. Частоту колебаний можно определить по формуле:

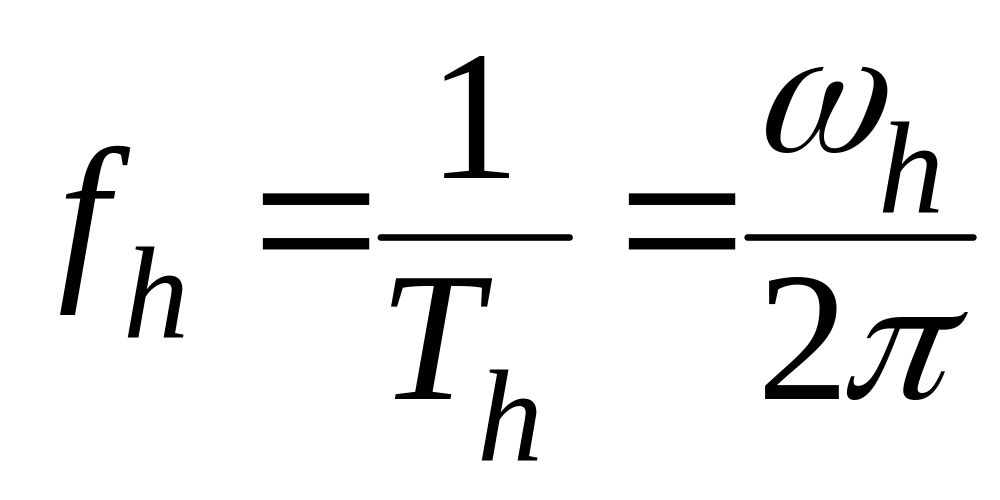
где T_h – расстояние между двумя смежными максимумами, условно называемое периодом колебаний.

Число колебаний связано с периодом колебаний и временем регулирования следующим примерным соотношением:

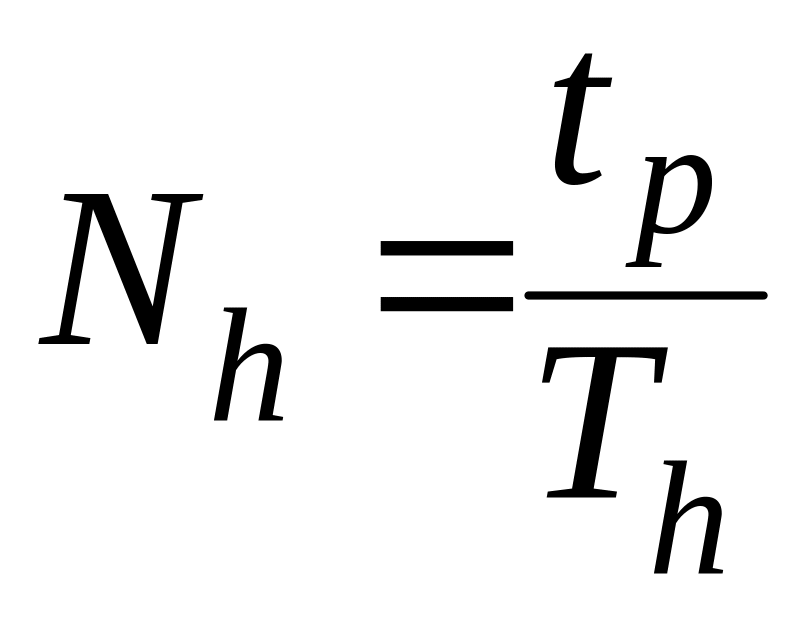
Требования к показателям качества переходного процесса можно представить графически в виде некоторой допустимой области протекания переходного процесса, за пределы которой управляемая величина не должна выходить (см. рис. 6.2).

Рисунок 6.2

Следует иметь в виду, что к качеству переходного процесса могут предъявляться и другие требования, например, время нарастания первого максимума t_m, максимальное ускорение управляемой величины на начальном участке нарастания h(t), т.е. h_мах(t) при 0< t< t_m и т.д.