6.5.2 Оценка качества сау по ее ачх а(ω)

если САУ минимально-фазовая, то качество можно оценить по одной АЧХ А(ω). В большинстве реальных САУ АЧХ А(ω) имеет вид, изображенный на рис. 6.9.

По АЧХ можно приближенно оценить колебательность и быстродействие системы.

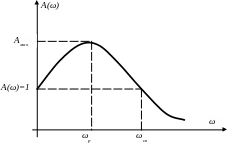
Рисунок 6.9

Колебательность системы определяется по величине показателя колебательности М, представляющего собой отношение максимального значения АЧХ А_мах замкнутой САУ к ее значению при ω = 0, т.е. М = А_мах/А(0). Для астатических САУ М = А_мах, так как А(0) = Р(0) = 1. Для статических САУ А(0) = Р(0) = К/(1+К), причем, если К ≥ 1, то в этом случае М ≈ А_мах. Поэтому часто показателем колебательности называют величину М = А_мах = |Ф(jω)|_мах. Чем больше М = А_мах, тем меньше запас устойчивости и тем более колебательный переходный процесс. При М → ∞ колебательность возрастает до получения незатухающих колебаний, соответствующих нахождению системы на границе устойчивости. Примером такой связи колебательности переходного процесса с максимумом АЧХ может служить колебательное звено. Большое число расчетов и экспериментов показало, что в хорошо демпфированных системах показатель колебательности не должен превышать значений М = 1,1-1,5, хотя иногда он может достигать М = 2-2,5. при М > 2 имеет место чрезмерная колебательность переходной составляющей процесса управления.

Для оценки быстродействия системы может использоваться резонансная частота ω_р, соответствующая максимальной ординате АЧХ, и во многих случаях близкая к частоте среза замкнутой системы ω_сз (см. рис. 6.9). так как частота колебаний переходной характеристики ω_к = 2πf_к примерно равна ω_р(ω_сз), то время достижения первого максимума переходной характеристикой равно примерно половине периода колебаний этой частоты, т.е t_m ≈ π/ω_р ≈ π/ω_сз. Если при этом предположим, что переходная характеристика системы в течение t_р имеет 1-2 колебания, то

Таким образом, показатель колебательности М = А_мах и характерные частоты ω_р, ω_сз замкнутой САУ так же, как Р_мах и , ω_п являются косвенными показателями качества переходного процесса.

В заключение заметим, что амплитудно-частотные характеристики А(ω) устойчивых систем по своему виду подобны АЧХ колебательного звена. Поэтому, если показатель колебательности М > 1, то замкнутую САУ можно аппроксимировать колебательным звеном, т.е. считать, что

Тогда

График М = f(ξ), соответствующий выражению (6.33), приведен на рис. 6.10а.

Для передаточной функции (6.31) на основе графиков h(t) можно установить зависимость перерегулирования σ и времени регулирования t_р от относительного коэффициента затухания ξ. Эти зависимости в виде кривых σ = f₁(ξ), t_р = f₂(ξ) изображены на рис. 6.10б. воспользовавшись графиками М = f(ξ) и σ = f₁(ξ) нетрудно найти зависимость перерегулирования σ от показателя колебательности М. эта зависимость представлена на рис. 6.10в.

Рисунок 6.10

Следовательно, для приближенной оценки показателей качества переходного процесса систем, АЧХ А(ω) которых близки к АЧХ колебательного звена, необходимо: а) по графику АЧХ А(ω) определить значение М и ω_р; б) войти по значению М в график рис. 6.10а и найти ξ; в) по значению ξ войти в график рис. 6.10б и определить искомые показатели σ в процентах % и t_р в nπ/ω_о, где ω_о=1/Т_о – собственная частота колебаний, определяемая по формуле ω_о=ω_р/ , которая вытекает из выражения ω_р=ω_о . заметим также, что перерегулирование может быть найдено и по показателю колебательности М из графика 6.10в.