6.3 Анализ качества переходного процесса

рассмотренные ранее показатели качества переходного процесса часто называются прямыми показателями, а методы, позволяющие построить переходную характеристику и определить по ней прямые показатели, - прямыми методами анализа. Основными из них являются: а) классический и операционный методы решения уравнений движения системы при Х(t) = 1(t) и нулевых начальных условиях; б) методы, основанные на использовании аналоговых и цифровых вычислительных машин (аналоговое и цифровое моделирование системы); в) приближенные методы построения переходной характеристики.

Из приближенных методов построения переходной характеристики наиболее широкое практическое применение получил разработанный в 1948 г. советским ученым В.В. Солодовниковым метод трапецеидальных частотных характеристик.

Кроме прямых методов анализа качества переходного процесса, в теории управления разработаны более удобные для инженерной практики косвенные методы оценки, часто называемые косвенными критериями качества переходных процессов. Они позволяют сравнительно просто, без построения кривой h(t), оценить не только качество системы, но и решать задачу выбора одного или нескольких параметров системы из условия обеспечения требуемого качества. В настоящее время существует следующие основные группы косвенных критериев качества: частотные, корневые и интегральные.

Наибольшее распространение получил косвенный метод оценки качества переходного процесса по вещественной ЧХ. Математической основой этого метода является связь между h(t) и ВЧХ Р(ω) системы.

6.4 Связь между вчх и переходной функцией системы

при изучении частотных характеристик систем и их элементов (см. лекцию 2) отмечалось, что они представляют собой формулы и соответствующие им графики, характеризующие реакцию системы (элемента) на гармонический входной сигнал в установившемся режиме. Однако, несмотря на это, частотные характеристики определяют и динамические свойства систем (элементов). Объясняется это тем, что между частотными и временными характеристиками существует связь, устанавливаемая с помощью преобразования Фурье. Одностороннее преобразование Фурье характеризуется формулами:

;

и является частным случаем преобразования Лапласа при р = jω, т.е. оно применимо для функций Х(t), удовлетворяющих условиям: Х(t) = 0 при t < 0, < ∞.

Ранее было показано, что w(t) = L [ Ф(р) ].

Поэтому, если САУ устойчива, то при р = jω получим

, (6.18)

где Ф(jω)=w(jω)= представляет собой изображение Фурье и является комплексной функцией частоты ω, которая определяет гармонический состав функции w(t). Функция Ф(jω) может быть найдена из передаточной функции Ф(р) подстановкой р = jω. Выражение (6.18) с учетом того, что

;

примет вид

отбрасывая в этом выражении мнимую часть (так как w(t) является вещественной), будем иметь

(6.19)

Подынтегральные выражения Р(ω)cosωt и Q(ω)sinωt представляют собой четные функции частоты ω. Поэтому интегрирование в пределах (-∞, ∞) можно заменить на (0, ∞) и удвоить результат. В этом случае (6.19) примет вид

(6.20)

Поскольку для момента времени t = -t, (т.е. t < 0) w(-t) = 0, cos(-ωt) = cosωt, sin(-ωt) = - sinωt, то можно, подставив в выражение (6.20) вместо t величину – t, записать

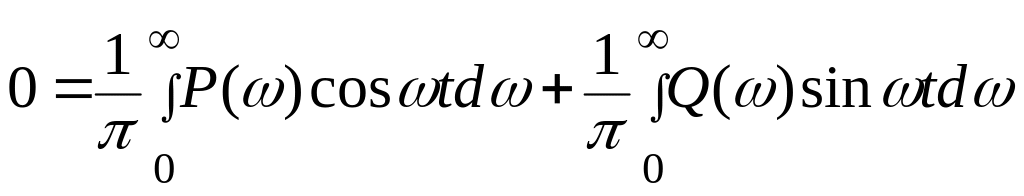(6.21)

Складывая выражения (6.20) и (6.21), получим

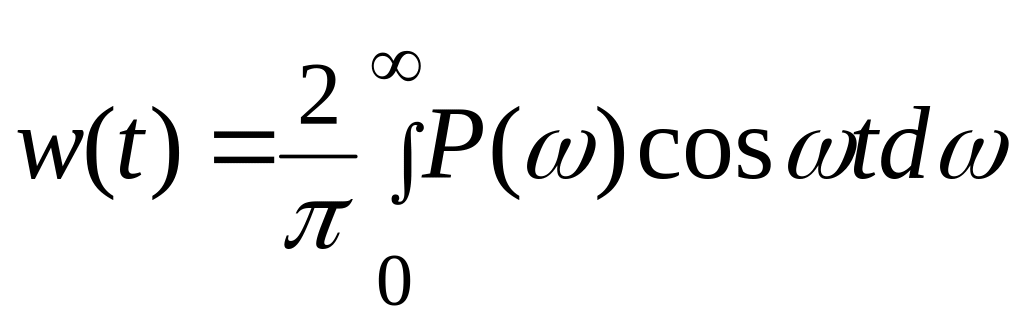(6.22)

Эта формула устанавливает связь между импульсной переходной функцией w(t) системы и ее ВЧХ р(ω). Учитывая, что

и интегрируя выражение (6.22), найдем

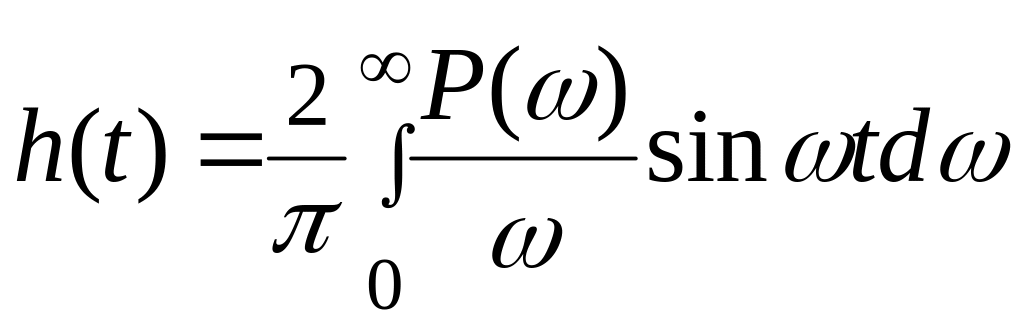(6.23)

т.е. найдем искомую связь между переходной функцией h(t) системы и ее ВЧХ Р(ω).

Если из выражения (6.20) вычесть выражение (6.21), то получим связь w(t) с Q(ω):

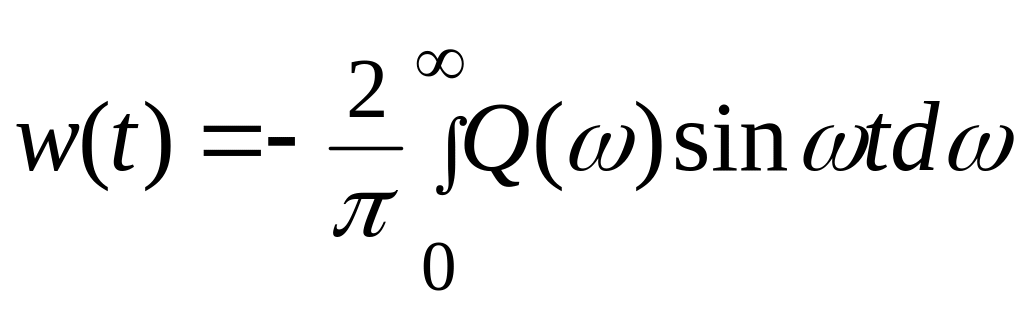(6.24)

Интегрируя (6.24) от 0 до t, найдем связь между h(t) и Q(t):

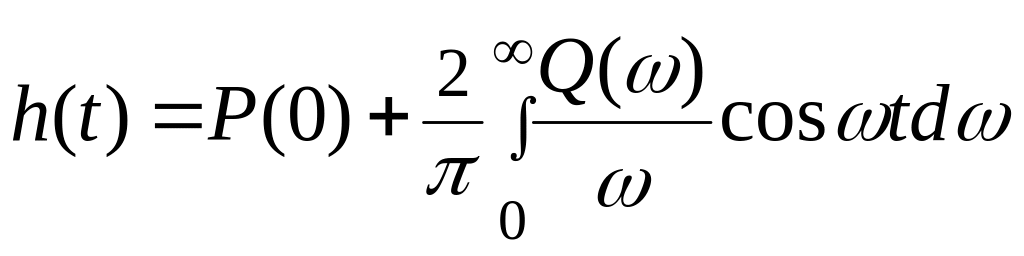(6.25)

где Р(0) – значение ВЧХ Р(ω) при ω = 0.

Полученные формулы (6.22) – (6.25) равноценны. Однако на практике особенно широко пользуются формулами, которые устанавливают связь w(t) и h(t) с Р(ω). В частности, формула (6.23) лежит в основе приближенного метода построения переходной характеристики h(t) САУ по известному графику ее ВЧХ Р(ω) и косвенного метода оценки качества переходного процесса САУ, вызванного задающим воздействием Х(t) = 1(t), по виду ВЧХ Р(ω).

Следует иметь ввиду, что временные характеристики w(t), h(t) имеют связь не только с ВЧХ Р(ω) и МЧХ Q(ω), но и с другими частотными характеристиками замкнутой и разомкнутой системы. Так, если в формулы (6.23) и (6.25) подставить Р(ω)=A(ω)cosφ(ω), Q(ω)=A(ω)sinφ(ω) и Р(0) = А(0), а затем формулы сложить, то после элементарных преобразований найдем:

(6.26)

если же в формулу (6.23) вместо Р(ω) подставить выражение

,

то получим

(6.27)

формулы (6.26) и (6.27) устанавливают связь h(t) с амплитудно-частотными и фазо-частотными характеристиками замкнутой и разомкнутой системы, и, следовательно, указывает на возможность оценки качества переходного процесса, вызванного задающим воздействием Х(t) = 1(t), по виду АЧХ и ФЧХ системы, как в замкнутом, так и в разомкнутом состоянии.