6.2.4 Определение установившихся ошибок астатических систем

А. астатическая САУ с ν_I = 0, ν_II = 0 и ν = ν_I + ν_II = 1, т.е. САУ, содержащая одно интегрирующее звено до точки приложения возмущения:

а) постоянные входные воздействия, т.е. Х(t) = Х₀1(t), f(t) = f₀1(t) или Х(р) = Х₀/р f(р) = f₀/р. Подставляя ν = I, ν_I = 1, Х(р) и f(р) в (6.8) и (6.9), получим = 0, = 0. следовательно, САУ с такой структурой является астатической первого порядка по отношению к задающему и возмущающему воздействиям;

б) скоростные входные воздействия, т.е. Х(t) = V_х t, f(t) = V_f t или Х(р) = V_х/р², f(р)= V_f/р². подставляя ν = 1, ν_I = 1, Х(р) и f(р) в (6.8) и (6.9), получим:

; (6.14)

(6.15)

где К = К_IК_II коэффициент передачи разомкнутой системы, имеющий размерность с^-1, называемой добротностью системы по скорости.

Установившуюся ошибку воспроизведения скоростного воздействия принято называть скоростной ошибкой, поэтому в формулах (6.14) и (6.15) принято обозначение . Из формул (6.14) и (6.15) видно, что установившиеся ошибки , и, следовательно, = + , создаваемые внешними воздействиями, изменяющимися с постоянной скоростью, можно уменьшить за счет увеличения коэффициента К₁. Увеличение этого коэффициента приводит, во-первых, к уменьшению и, во-вторых, к увеличению коэффициента К, а значит к уменьшению . Однако, как уже отмечалось, такой способ повышения точности САУ связан с ухудшением ее устойчивости;

в) равноускоренные входные воздействия, т.е. Х(t) = а_х t², f(t) = а_f t² или Х(р) = 2а_х/р³, f(р)= 2а_f/р³. подставляя ν = 1, ν_I = 1, Х(р) и f(р) в (6.8) и (6.9), получим: = ∞, = ∞.

Это значит, что внешние воздействия, изменяющиеся с постоянным ускорением, создают установившиеся ошибки и , которые со временем t → ∞ увеличиваются до бесконечности.

Следовательно, САУ, содержащие в одноконтурной структурно-динамической схеме одно интегрирующее звено до точки приложения возмущения, будут выполнять свои функции в том случае, если внешние воздействия постоянны или изменяются с постоянной скоростью. Примерами таких САУ могут служить следящие системы, работающие в режиме слежения с постоянной скоростью, системы программного обеспечения, к которых Х_пр(t) изменяется по закону, близкому к скоростному воздействию, а также системы стабилизации, к которым предъявляются требования, чтобы = 0.

Б. астатическая САУ ν_I = 0, ν_II = 1 и ν =ν_I + ν_II = 1, т.е. САУ, содержащая одно интегрирующее звено за точкой приложения возмущения:

а) постоянные входные воздействия, т.е. Х(t) = Х₀1(t), f(t) = f₀1(t) или Х(р) = Х₀/р f(р) = f₀/р. Подставляя ν = 1, ν_I = 0, Х(р) и f(р) в (6.8) и (6.9), получим = 0, а

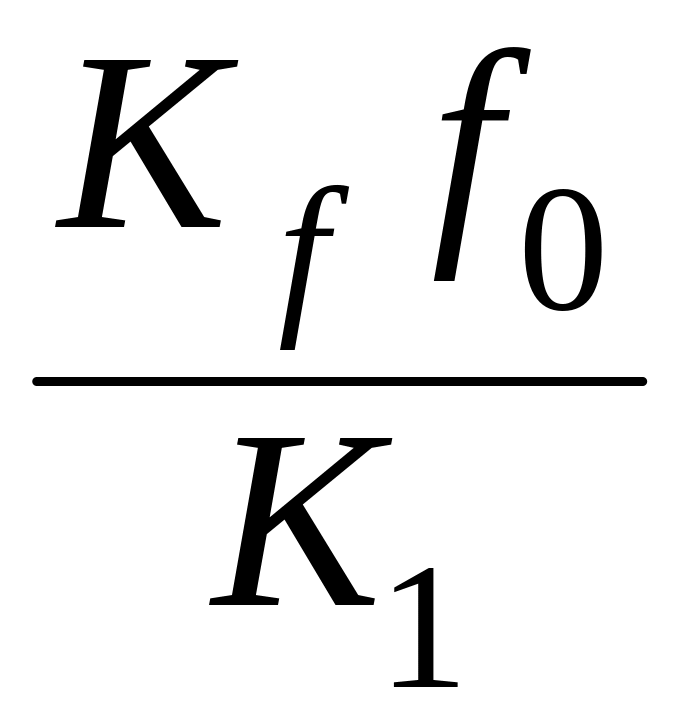= (6.16)

следовательно, САУ с такой структурой является астатической первого порядка по отношению к задающему воздействию, а по отношению к возмущению будет статической. При этом величина этой САУ не равна статической САУ, что видно из сопоставления формул (6.13) и (6.16);

б) если к этой системе приложены одновременно задающее воздействие Х(t) = V_х t и возмущение f(t) = V_f t, то нетрудно убедиться в том, что = V_х/К, = ∞ и, следовательно, = ∞. Это значит, что САУ с одним интегрирующим звеном, расположенным за точкой приложения возмущения, обеспечивает воспроизведение скоростного задающего воздействия с точностью, определяемой такой же скоростной ошибкой, что и система с одним интегрирующим звеном, расположенным до точки приложения возмущения. Однако, она неспособна скомпенсировать действие возмущения, изменяющегося с постоянной скоростью. Если к этой системе приложено задающее воздействие Х(t) = а_х t², т.е. задающее воздействие, изменяющееся с постоянным ускорением, то оно будет создавать = ∞. Поэтому, САУ с такой структурой могут найти применение для воспроизведения Х(t) = V_х t в условиях действия постоянных возмущений. Примером может служить следящая система, работающая в режиме слежения с постоянной скоростью при f(t) = const.

Анализ полученных выше результатов для двух астатических САУ с различным методом расположения одного интегрирующего звена позволяет сделать следующий очень важный для практики вывод: порядок астатизма системы по отношению к задающему воздействию определяется числом ν = ν_I + ν_II, т.е. числом интегрирующих звеньев, содержащихся в однокон-турной структурно-динамической схеме системы, а по отношению к возмущающему воздействию – числом ν_I, т.е. числом интегрирующих звеньев, расположенных между входом системы и точкой приложения этого возмущения.

В. В заключение рассмотрим определение ошибок , САУ с ν_I = 1, ν_II = 1, ν = ν_I + ν_II = 2. эта система по отношению к задающему воздействию является астатической второго порядка (ν = ν_I + ν_II = 2), а по отношению к возмущению – астатического первого порядка (ν_I = 1). Поэтому при воздействиях Х(t) = V₀ 1(t), f(t) = f ₀ 1(t) имеем = = 0; при воздействиях Х(t) = V_х t, f(t) = V_f t точность работы этой системы будет определяться только = K_fV_f/K_I, т.к. наличие в одноконтурной структурно-динамической схеме двух последовательно соединенных интегрирующих звеньев приводит к тому, что = 0. если у этой системе будут приложены Х(t) = а_х t² и f(t) = а_f t², то, согласно формулам (6.8) и (6.9),

(6.17)

а = ∞. Это значит, что задающее воздействие, изменяющееся с постоянным ускорением а_х, создает постоянную установившуюся ошибку, величина которой определяется по формуле (6.17). эта ошибка характеризует точность воспроизведения системой равноускоренного воздействия. Ее принято называть ошибкой от ускорения, а коэффициент передачи К, входящий в формулу (6.17) и имеющий размерность с^-2 (ν = 2) – коэффициентом передачи (добротностью) системы по ускорению. Так как возмущающее воздействие, изменяющееся с постоянным ускорением а_f, создает установившуюся ошибку, стремящуюся к бесконечности, то САУ с такой структурой могут найти применение для воспроизведения Х(t) = а_хt² в условиях действия постоянных возмущений или возмущений, изменяющихся с постоянной скоростью. Примером может служить следящая система, работающая в режиме слежения с постоянным ускорением при постоянных возмущающих воздействиях и при возмущениях, изменяющихся с постоянной скоростью.

Нетрудно убедиться в том, что если на вход астатической системы с ν_I = 1, ν_II = 1 поступает задающее воздействие, описываемое кубической функцией времени, то = ∞. Это значит, что такое воздействие система воспроизвести не может. Для его воспроизведения с постоянной установившейся ошибкой необходимо ввести еще одно последовательное интегрирующее звено, т.е. создать астатическую систему третьего порядка.

На практике при оценке точности САУ с единичной ООС (определением установившихся ошибок) следует придерживаться следующего порядка решения задач:

а) определить порядок астатизма системы по отношению ко всем воздействиям (т.е. количество интегрированных звеньев ν_I, ν_II и ν);

б) определить, какой будет установившаяся ошибка при заданном воздействии (ноль, постоянная величина или бесконечность);

в) если ошибка равна постоянной величине, выбрать соответствующую формулу и определить численное значение ошибки.