Лекция 5 анализ устойчивости линейных непрерывных стационарных систем

5.1 Понятие об устойчивости линейной стационарной системы,

необходимое и достаточное условие устойчивости

основы теории устойчивости движения любых динамических систем, поведение которых описывается обыкновенными дифференциальными уравнениями, были разработаны великим русским ученым академиком А.М.Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Сущность определения устойчивости движения по А.М.Ляпунову состоит в следующем: невозмущенное движение системы называется устойчивым, если при всех t > t₀ отклонение возмущенного движения от невозмущенного сколь угодно мало при достаточно малых начальных возмущениях в момент t₀; невозмущенное движение системы называется асимптотически устойчивым, если отклонение возмущенного движения от невозмущенного стремится к нулю при t → ∞.

В теории управления за невозмущенное движение линейной стационарной САУ обычно принимают установившееся состояние (установившийся статистический или динамический режим), а за возмущенное – неустановившееся движение, т.е. переходный процесс. При этом для линейных стационарных САУ практическое значение имеет асимптотическая устойчивость. Поэтому, в соответствии с понятием устойчивости по А.М.Ляпунову, линейная стационарная САУ называется асимптотически устойчивой, если она обладает свойством возвращаться с течением времени в исходное установившееся состояние после прекращения действия тех возмущений, которые вывели ее из этого состояния. Иначе говоря, асимптотическая устойчивость (в дальнейшем для краткости слово «асимптотическая» будем опускать) линейных стационарных систем связана с их собственным движением. Математически это движение описывается выражением вида:

, (5.1)

в котором p_i являются корнями характеристического уравнения замкнутой САУ

(5.2)

или характеристического уравнения разомкнутой системы

(5.3)

ранее было показано, что если в характеристических уравнениях (5.2) и (5.3) все корни имеют отрицательные вещественные части, то

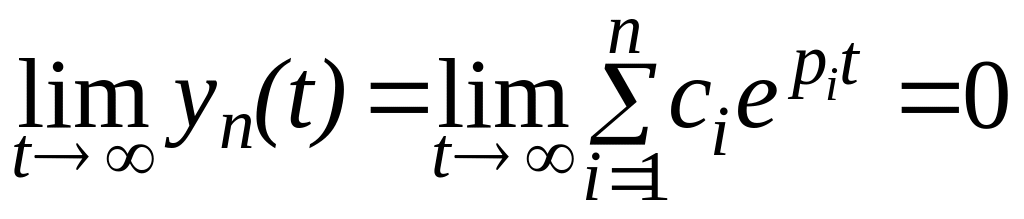(5.4)

и система будет устойчива.

Следовательно, необходимым и достаточным условием устойчивости линейной (линеаризованной) стационарной системы является отрицательность вещественных частей всех корней ее характеристического уравнения. Наличие в характеристическом уравнении хотя бы одного корня с положительной вещественной частью означает, что система неустойчива. Если среди корней характеристического уравнения имеется пара чисто мнимых корней или один нулевой корень, а вещественные части всех остальных корней отрицательны, то система находится на колебательной или апериодической границе устойчивости. В характеристическом уравнении (5.2) наличие одного нулевого корня возможно лишь при условии a₀ = 0. однако в физически реализуемых системах характеристический многочлен А(р) является полным многочленом: в статистических САУ ( = 0) a₀ = 1 + К, а в статистических САУ ( ≠ 0, т.е. = 1, = 2, …) a₀ = К. А это означает, что замкнутая САУ может находится только на колебательной границе устойчивости.

В отличие от характеристического уравнения (5.2) замкнутой САУ, характеристическое уравнение (5.3) разомкнутой системы может содержать как чисто мнимый, так и нулевой корень, т.е. разомкнутая система может находиться как на колебательной, так и на апериодической границе устойчивости.