3.4.2 Построение дискриминационной модели

Построение дискриминантной модели заключается в расчете и анализе коэффициентов дискриминантной функции. Построенная дискриминантная модель должна максимально четко разделять исследуемые группы. Качество построенной дискриминантной модели в рассматриваемом примере характеризуется данными, представленными в таблицах 17 и 18:

Таблица 17

Собственные значения
Функция	Собственное значение	% объясненной дисперсии	Кумулятивный %	Каноническая корреляция
1	,084a	100,0	100,0	,279
a. В анализе использовались первые 1 канонические дискриминантные функции.

Примечание – Источник: Собственная разработка на основе программы SPSS.

Значение коэффициента корреляции между рассчитанными значениями дискриминантной функции и реальной принадлежностью к группе 0,279 является неудовлетворительным.

В таблице также представлен такой показатель, как собственное значение дискриминантной функции. Высокое значение этого показателя свидетельствует о высокой точности построенной дискриминантной модели. В нашем случае этот показатель имеет весьма низкое значение 0,084, что является негативным фактором.

Таблица 18

Лямбда Уилкса
Проверка функции(й)	Лямбда Уилкса	Хи-квадрат	ст.св.	Знч.
1	,922	28,921	3	,000

Примечание – Источник: Собственная разработка на основе программы SPSS.

Показатель «Лямбда Уилкса» используется для проведения теста на значимость различий средних значений дискриминантной функции в исследуемых группах. В нашем анализе значение показателя составляет 0,000, что свидетельствует о высокой значимости различий средних значений.

Таблица 19

Нормированные коэффициенты канонической дискриминантной функции
	Функция
	1
7) Сколько раз за последний месяц Вы бесплатно скачивали электронную литературу?	,633
зачем платить,если можно бесплатно скачать	-,640
18) Ваш возраст:	,421

Примечание – Источник: Собственная разработка на основе программы SPSS.

При помощи стандартизированных коэффициентов дискриминантной функции, представленных в таблице 8, можно оценить относительный вклад каждой дискриминационной переменной в различие двух исследуемых групп. В нашем анализе между переменными “сколько раз за последний месяц бесплатно скачивали электронную литературу” и “зачем платить, если можно бесплатно скачать” очевидно наибольшее влияние количества скаченной за последний месяц литературы и чуть меньшее влияние возраста читателя на покупку ее в интернете.

Таблица 20

Структурная матрица
	Функция
	1
зачем платить,если можно бесплатно скачать	-,661
18) Ваш возраст:	,565
7) Сколько раз за последний месяц Вы бесплатно скачивали электронную литературу?	,535
Объединенные внутригрупповые корреляции между дискриминантными переменными и нормированными каноническими дискриминантными функциями. Переменные упорядочены по абсолютной величине корреляций внутри функции.

Примечание – Источник: Собственная разработка на основе программы SPSS.

Корреляционные коэффициенты, представленные в таблице 20 позволяют оценить, насколько сильна связь дискриминационных переменных со стандартизированными значениями дискриминантной функции.

Таблица 21

Коэффициенты канонической дискриминантрой функции
	Функция
	1
7) Сколько раз за последний месяц Вы бесплатно скачивали электронную литературу?	,682
зачем платить,если можно бесплатно скачать	-1,366
18) Ваш возраст:	,758
(Константа)	-2,048
Ненормированные коэффициенты

Примечание – Источник: Собственная разработка на основе программы SPSS.

Нестандартизированные коэффициенты дискриминантной функции, представленные в таблице 21 используются для построения дискриминантной модели.

Полученная в результате анализа дискриминантная модель, имеет следующий вид:

d = -2,048 + 0,682x₁ – 1,366х₂ + 0,758х₃ ,

где x₁ – сколько раз за последний месяц бесплатно скачивали электронную литературу;

х₂ - зачем платить, если можно скачать бесплатно;

х₃ – возраст.

Построенная дискриминантная модель должна как можно более четко разделять исследуемые группы. Четкость разделения исследуемых групп характеризуется расстоянием между средними значениями дискриминантной функции в исследуемых группах (таблица 22).

Таблица 22

Функции в центроидах групп
Покупаю в интернете	Функция
	1
нет	-,139
да	,601
Ненормированные канонические дискриминантные функции вычислены в центроидах групп.

Примечание – Источник: Собственная разработка на основе программы SPSS.

Как видно из данных, представленных в таблице 22, средние значение дискриминантной функции для читателей, покупающих электронную литературу в интернете, составляет -0,139, а среднее значение дискриминантной функции для читателей, не покупающих ее в интернете, составляет 0,601. Чем больше расстояние между средними значениями дискриминантной функции в исследуемых группах, тем более четко прослеживается различие между исследуемыми группами.

Четкость различия между исследуемыми группами зависит также от рассеяния значений дискриминантной функции в исследуемых группах. Это рассеяние показано на графиках распределения значений дискриминантной функции в исследуемых группах (рис. 16 и 17).

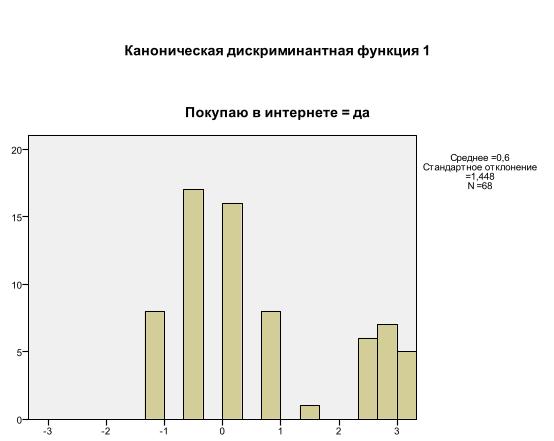
Рис. 16 - Распределение значений дискриминантной функции для группы читателей, покупающих электронную литературу в интернете.

Примечание – Источник: Собственная разработка на основе программы SPSS.

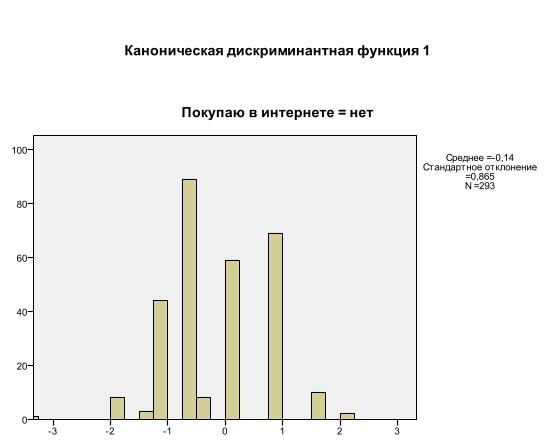
Рис. 17 - Распределение значений дискриминантной функции для группы читателей, не покупающих электронную литературу в интернете.

Примечание – Источник: Собственная разработка на основе программы SPSS.

На полученных графиках видно, что рассеяние значений дискриминантной функции в исследуемых группах достаточно большое. Следовательно, сложно однозначно определить принадлежность респондента к одной из исследуемых групп.

Также, согласно представленным данным, можно сделать вывод о том, что исследуемая группа “читатели, покупающие электронную литературу в интернете” входят 68 человек. В группу “читатели, не покупающие электронную литературу в интернете” входят 293 человека.