Исследовательская часть
Исследуем
точность метода Рунге-Кутта и метода
Эйлера на примере дальности неуправляемого
ЛА 
.
Точность в этих методах определяется
заданием шага интегрирования 
.
Будем 
последовательно
делить на 2, если точность велика, и
последовательно
умножать на 2, в случае, если точность
удовлетворяет (см. табл.7).
Таблица 7
|
Δt |
Дальность хп,м |
Метод Рунге-Кутта |
2*Δt=0.02 |
10300 |
Δt=0.01 |
10180 |
|
Δt/2=0.005 |
10170 |
|
Метод Эйлера |
2*Δt=0.02 |
10071 |
Δt=0.01 |
10143 |
|
Δt/2=0.005 |
10178 |
По
табл. 7 видно, что шаг 
выбран
верно, так как при 
изменение
значения дальности полета неуправляемого
ЛА незначительно, а при 
изменение дальности полета существенно.
Исследуем
поведение функции 
в зависимости от времени t
при постоянном значение коэффициента
лобового сопротивления Cx.
В качестве значений Сх возьмем:0.157,0.292.
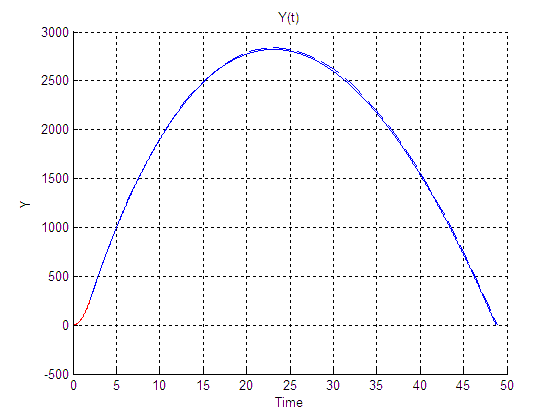
Y(t):
Cx=0.157
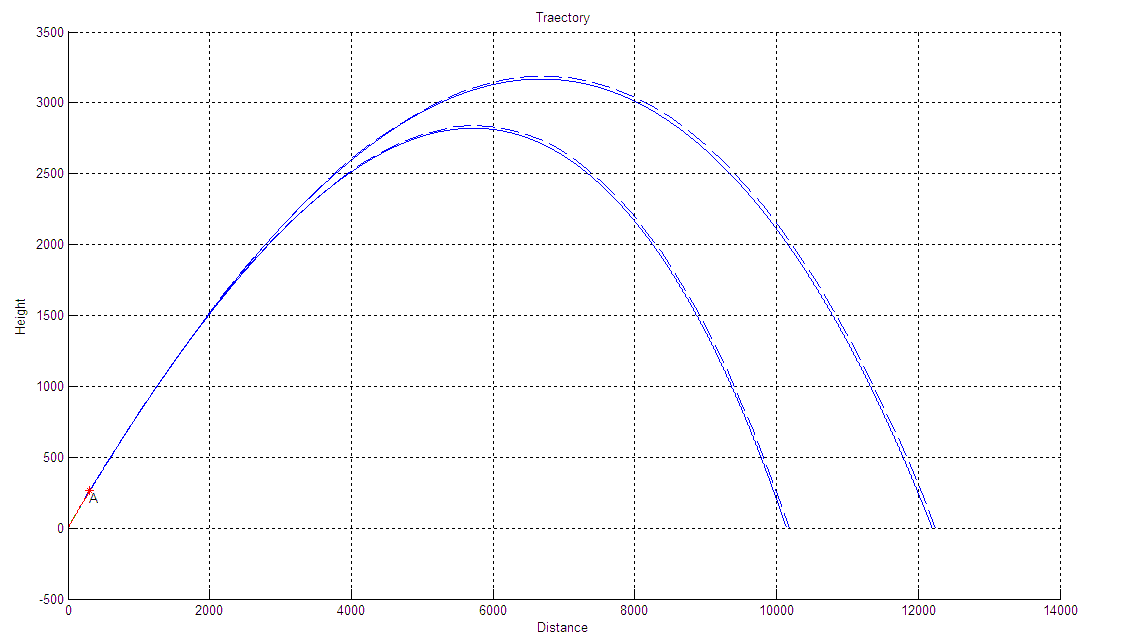
Сх=0.567
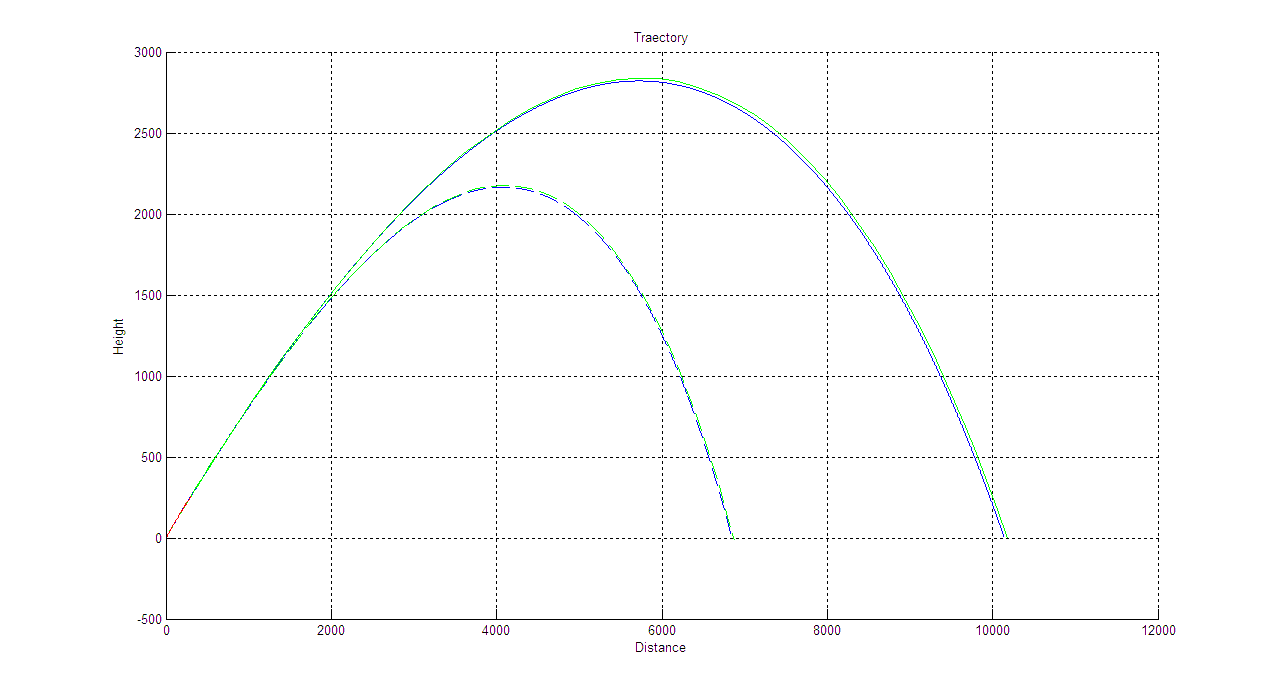
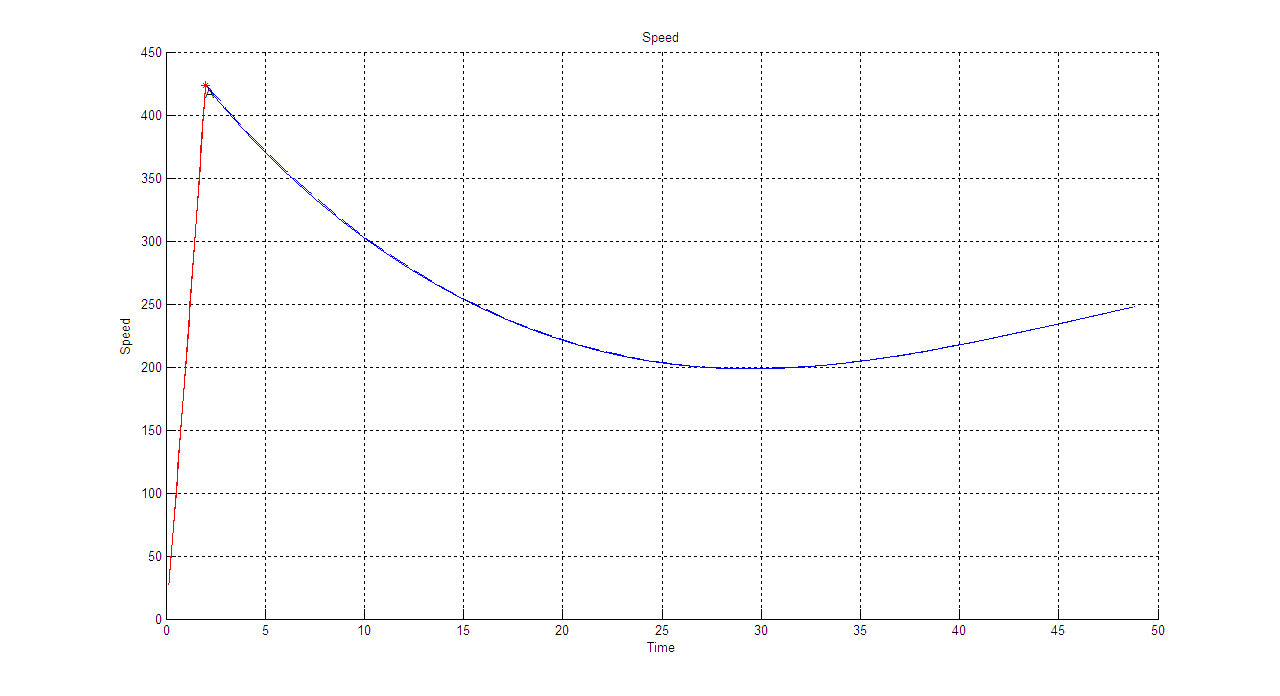
V(t):
Cx=0.157
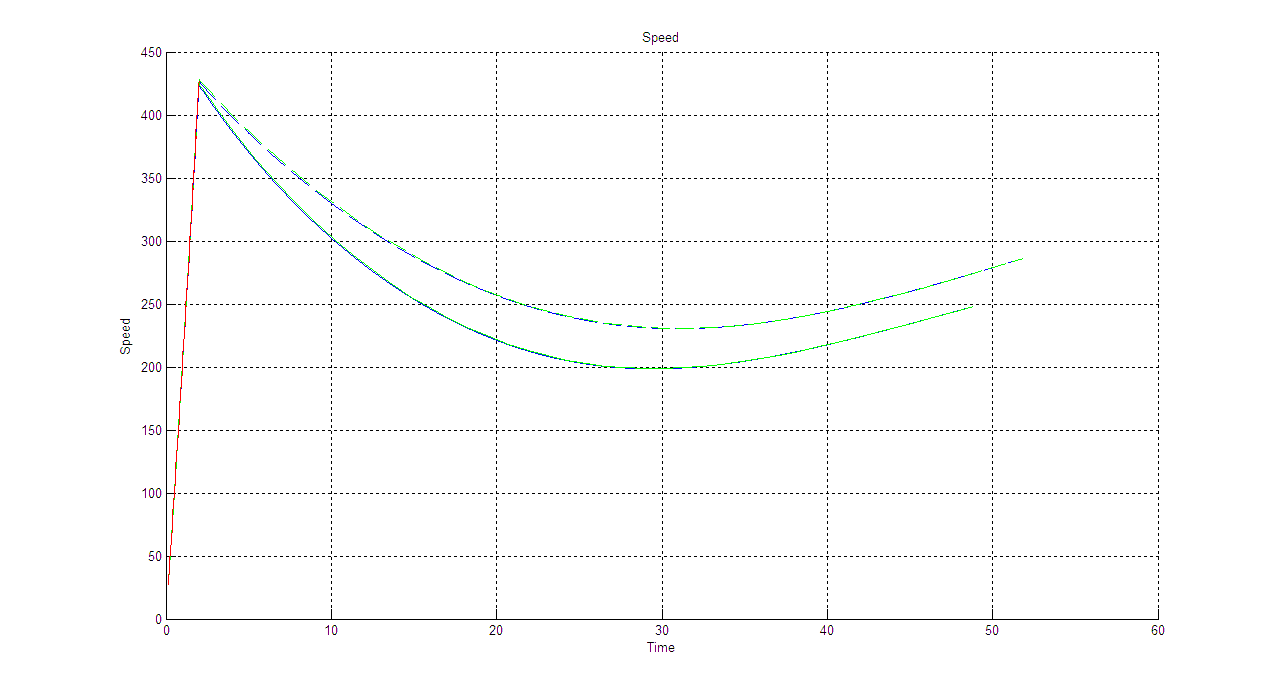
Cx=0.567
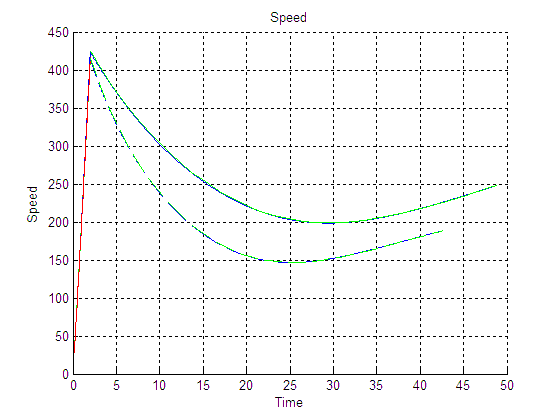
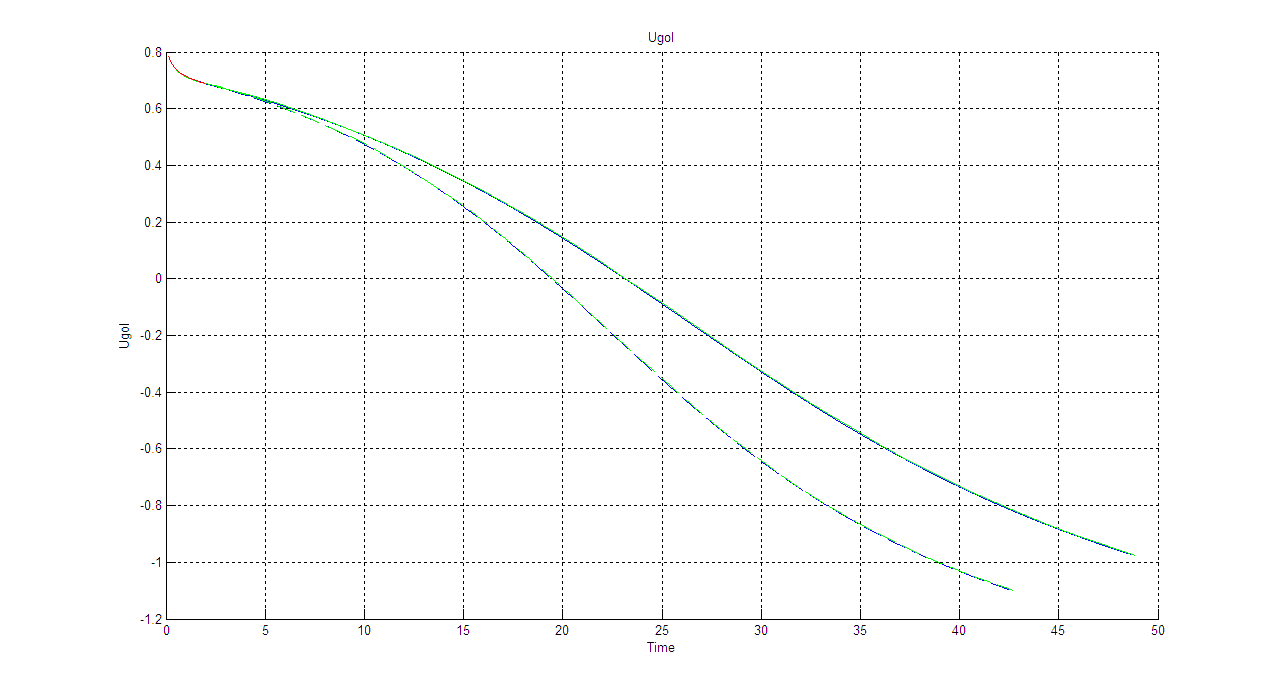
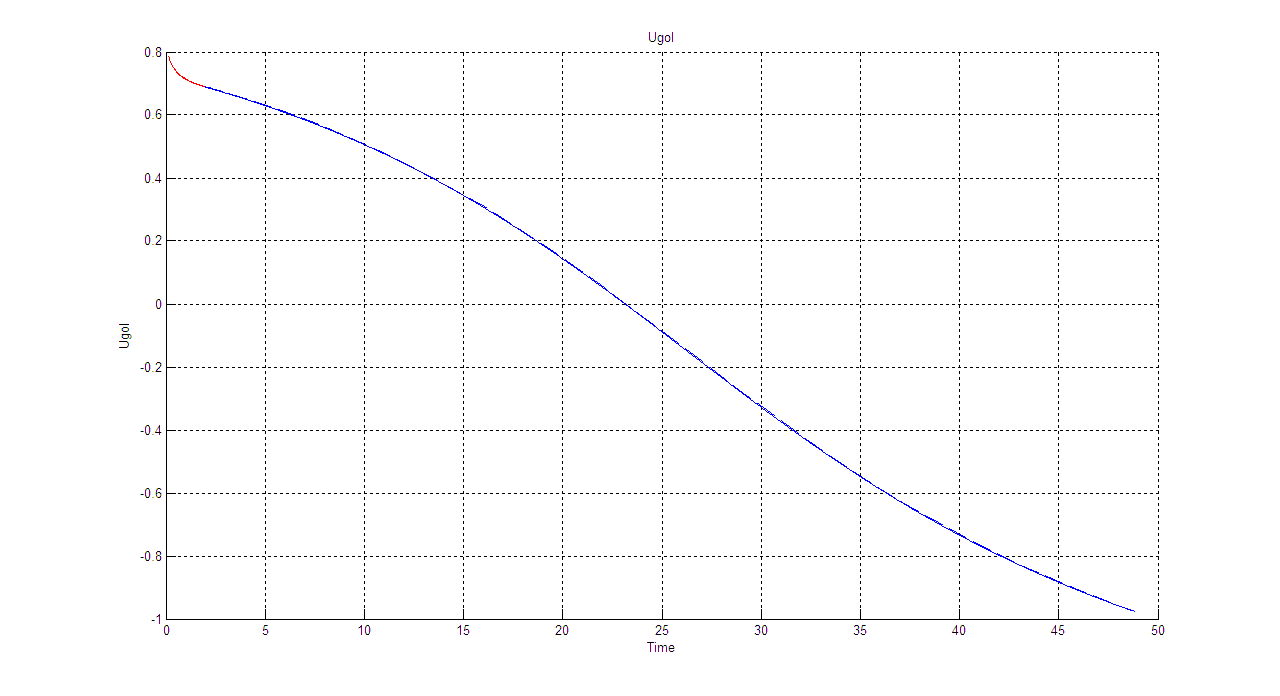
Θ(t):
Cx=0.157
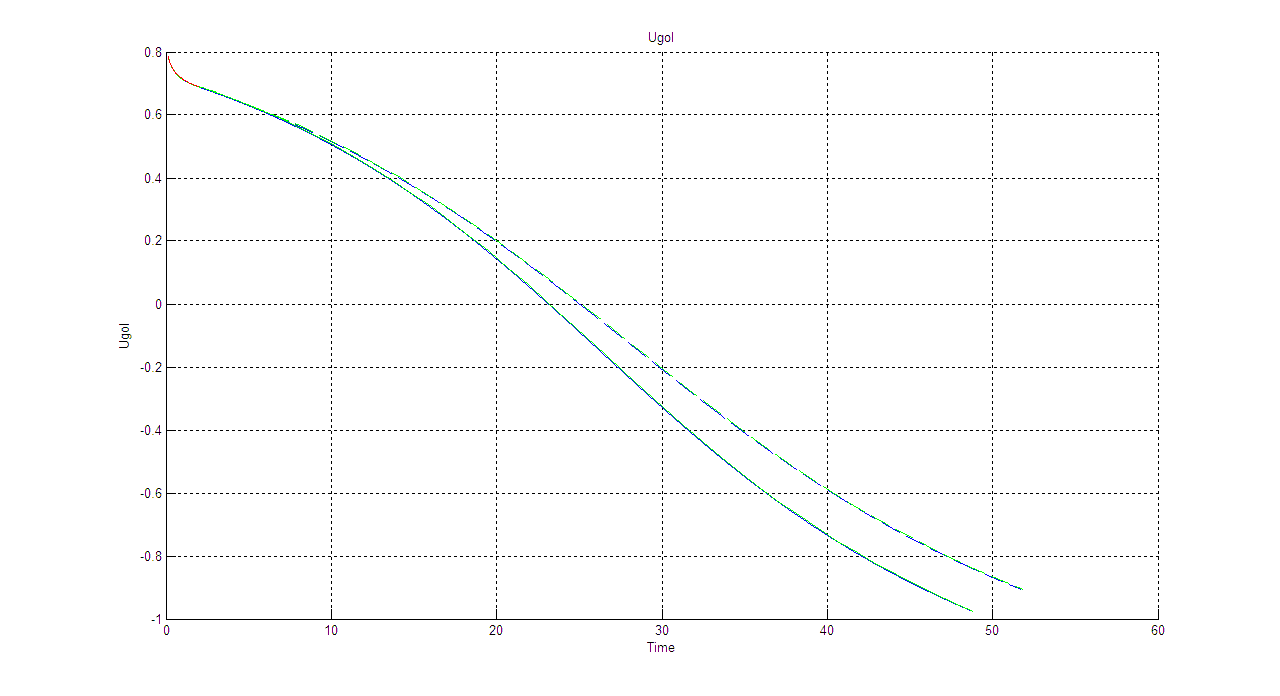
Cx=0.567
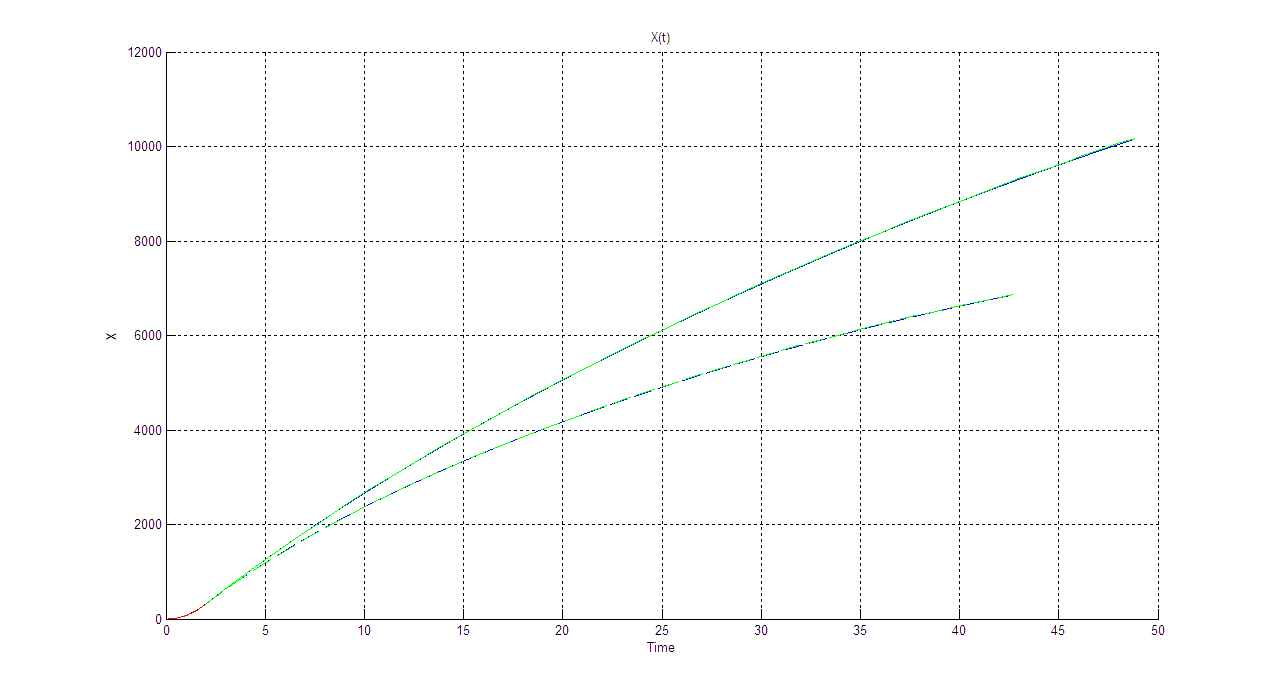
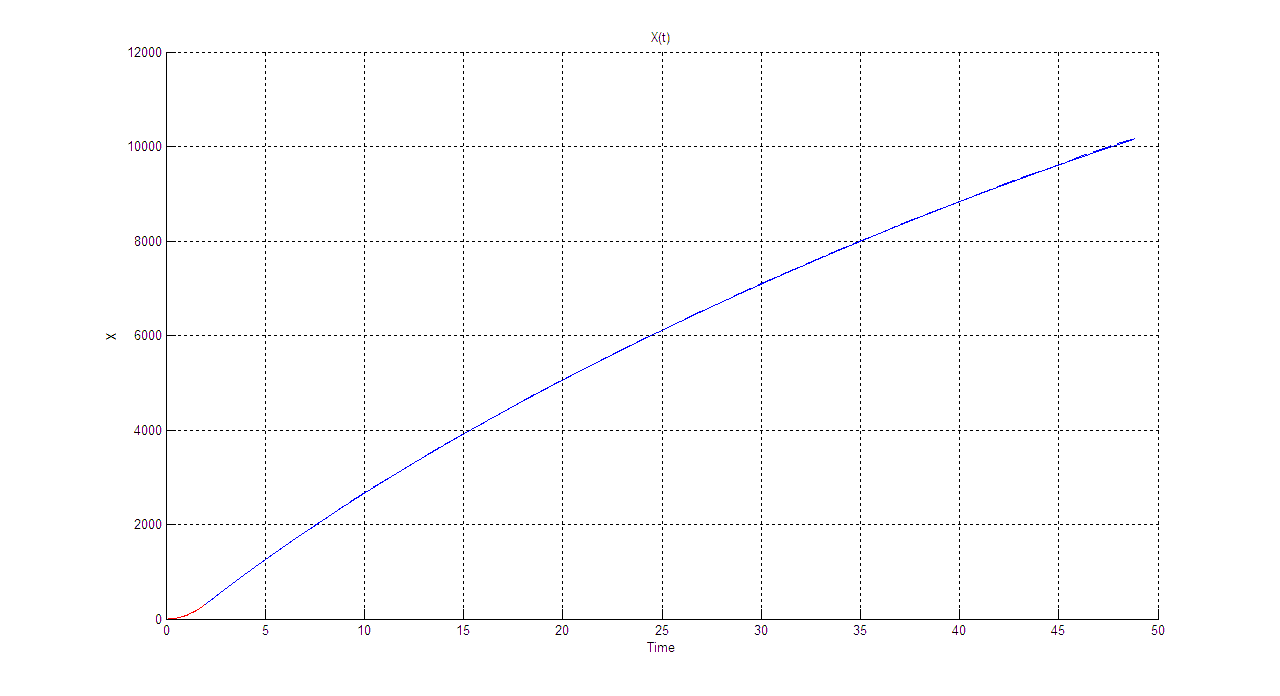
X(t):
Cx=0.157
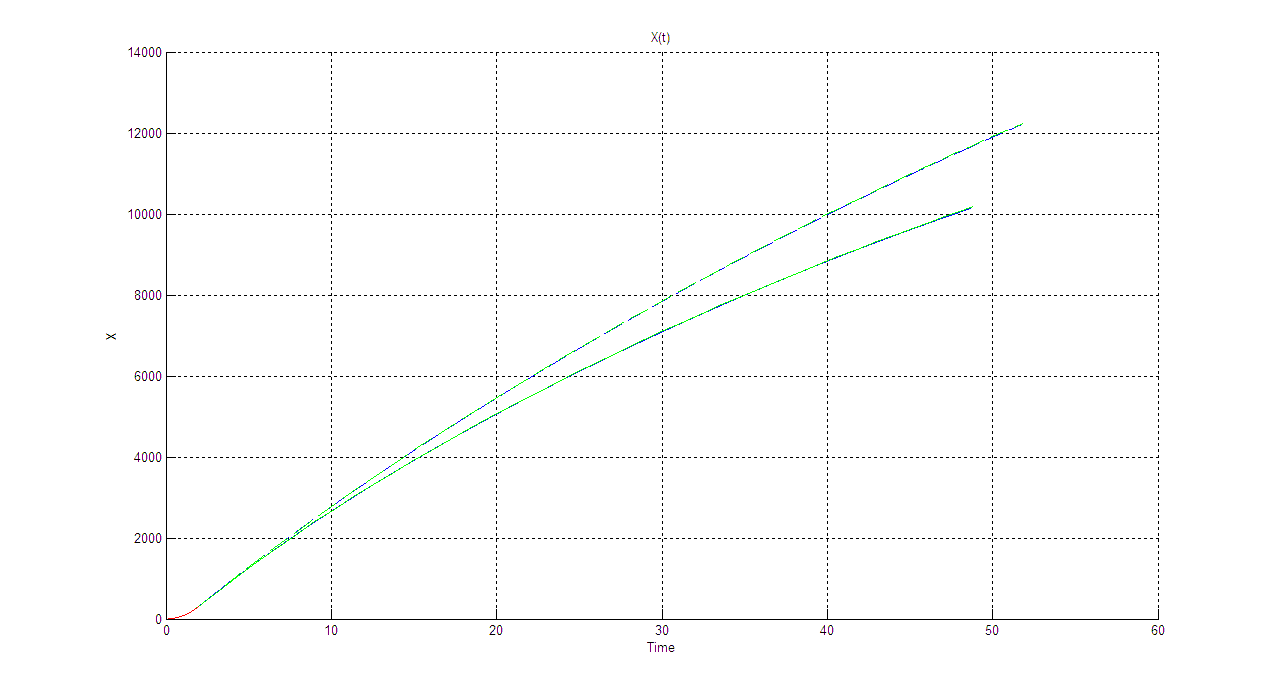
Cx=0.567
Приложение
Траектория неуправляемого летательного аппарата
Зависимость y(t):
V(t):
Θ(t):
X(t):
Y(t):
Программа рассчета методом Эйлера:
Метод Эйлера:
function [ t1,y] = metodEiler( F,t0,tk,y0 )
global h
if isempty(h); h=0.01; end
t=t0:h:tk;
t=t';
t1(1)=t0;
y(1,1)=y0(1);p(1,1)=y0(1);
y(1,2)=y0(2);p(1,2)=y0(2);
y(1,3)=y0(3);p(1,3)=y0(3);
y(1,4)=y0(4);p(1,4)=y0(4);
for i=1:length(t)-1
p(i+1,:)= y(i,:)+h*F(t(i,1),y(i,:));
if p(i+1,4)<=0
break
else
y(i+1,:)=p(i+1,:);
t1(i+1)=t1(i)+h;
end
end
t1=t1';
end
Функция правой части:
function F = rparts2(t,y,R)
V = y(1);
TT = y(2);
g = 9.8;
S=0.03462;
w=18;
i=1.8;
Cxet=0.157;
Cx=i*Cxet;
r0=1.23*exp(-2.5*sin(0.7854)/7800);
X = 0.5*Cx*r0*V^2*S;
m0start = 110;
timeDU = 1.8;%время горения топлива
empty_mass=m0start-w;
Q = (m0start - empty_mass)/timeDU;
if(R>0)
m = m0start - Q*t;
else
m = empty_mass;
end
F(1) = (R - X - m*g*sin(TT))/m;
F(2) = -g*cos(TT)/V;
F(3) = V*cos(TT);
F(4) = V*sin(TT);
End
Исполнительный файл:
t0=0.17;
g = 9.81;
R = 20000;
Ttopl = 1.8;
y0 = [29.482 0.785 1.414 1.414];
ta=Ttopl-t0;
rparts2(t0,y0,R)
[Ta,ResA] = metodEiler(@(t,y) rparts2(t,y,R),t0,ta,y0);
%начало пассивного(условие окончания у=0)
Za = ResA(end, :)
[Tp,ResP] = metodEiler(@(t,y) rparts2(t,y,0),ta,200,Za);
Zp = ResP(end, :)
Промежуточные результаты:
27.7149 0.7854 1.4142 1.4142
29.6744 0.7829 1.6102 1.6102
31.6361 0.7806 1.8205 1.8195
45.4278 0.7674 3.6994 3.6564
47.4065 0.7658 4.0264 3.9718
49.3873 0.7643 4.3681 4.3004
91.4612 0.7420 15.0092 14.2421
93.4872 0.7412 15.6834 14.8602
101.6113 0.7382 18.5348 17.4638
103.6473 0.7375 19.2864 18.1476
105.6854 0.7368 20.0535 18.8445
231.5623 0.7090 95.4021 84.8841
238.0369 0.7081 100.7254 89.4475
414.2723 0.6893 297.0540 253.8474
423.4713 0.6886 309.9509 264.4706
1.0e+004 *
0.0423 0.0001 0.0310 0.0264
0.0423 0.0001 0.0313 0.0267
0.0422 0.0001 0.0333 0.0283
0.0351 0.0001 0.1634 0.1267
0.0350 0.0001 0.1637 0.1269
0.0233 0.0000 0.4574 0.2679
0.0233 0.0000 0.4594 0.2686
0.0199 -0.0000 0.7279 0.2527
0.0199 -0.0000 0.7292 0.2522
0.0199 -0.0000 0.7294 0.2521
0.0199 -0.0000 0.7296 0.2520
0.0199 -0.0000 0.7298 0.2519
0.0199 -0.0000 0.7300 0.2519
0.0247 -0.0001 1.0122 0.0029
0.0247 -0.0001 1.0135 0.0011
0.0247 -0.0001 1.0136 0.0009
0.0248 -0.0001 1.0141 0.0003
0.0248 -0.0001 1.0142 0.0001