
- •Тема1. Задача про максимальний потік на мережі
- •Тема2: Сіткові графи
- •Варіанти завдань
- •Тема3. Прийняття рішень в умовах невизначеності та ризик
- •Тема4. Детерміновані моделі управління запасами
- •Тема5. Динамічні моделі управління запасами
- •Тема6. Імовірнісні моделі управління запасами з неперервним контролем рівня запасу
- •Тема7. Ієрархічні моделі прийняття рішень
- •8. Спеціалізовані системи обслуговування з пуассонівським розподілом
Тема6. Імовірнісні моделі управління запасами з неперервним контролем рівня запасу
Задача 1
Виходячи з умови та розв’язку завдання 1 лабораторної роботи №6, визначте розмір резервного запасу таким чином, щоб імовірність виснаження запасу не перевищувала =0.05 за умови, що денний попит є нормально розподіленою випадковою величиною з математичним сподіванням D кг м’ясного фаршу і середньоквадратичним відхиленням =0.1D кг м’ясного фаршу.
Дано
=0.05
D=(2+3P/2)+100=111
=0,1*D=11
L=W=7
Розв’язання
P(XL≥µL+B)≤
B≥K*L
Згідно умов задачі =0.05
µL=D*L=111*7=777
L=√2*L,
L=√11*7=√77=8,77
K - з таблиці стандартного, нормального розподілу знаходимо
K0,05=1,64
В= K*L=1,64*8,77=14,38≈14
Задача 2
Завдання 2. Вирішіть задачу з прикладу 2 у припущенні, що попит у період виконання замовлення є випадковою величиною, рівномірно розподіленою на інтервалі [0, 67] (галонів), де S=4–номер варіанту,W=7–кількість букв імені,P=6–кількість букв в прізвищі
Розв’язання: Стохастична модель.
Скористаймось
наближеним алгоритмом знаходження
оптимального розв’язку описаної задачі.
Перед знаходженням оптимального
розв’язку перевіримо чи існує допустимий
розв’язок задачі: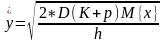
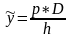
р=10, D=1000, h=2, K=100
Оскільки
попит є випадковою величиною рівномірно
розподіленою в діапазоні від о до 67, то
М{х}=33.5
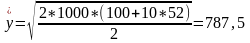 галонів
галонів
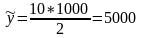 галонів
галонів
Оскільки
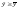 ,
то існує єдиний розв’язок для
,
то існує єдиний розв’язок для
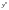 і
і
 .
Вираз для S
записується в наступному вигляді:
.
Вираз для S
записується в наступному вигляді:
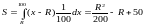 .
.
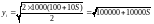 галонів,
галонів,
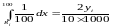 .
.
З
останнього рівняння маємо
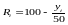 .
.
Тепер використовуємо рівняння (3) і (4) для знаходження розв’язку.
Ітерація1.
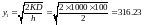 галонів R1=100-
галонів R1=100-
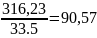 галонів
галонів
Ітерація
2.
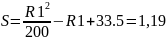 галонів. Y2=
галонів. Y2=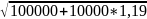 =334,51
=334,51
Отже,
R2=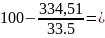 90,02
галонів
90,02
галонів
Ітерація
3. S=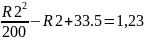 ,
Y3=
,
Y3=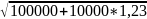 =335,11
=335,11
R3=100-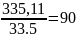
Оскільки значення R2 і R3 приблизно однакові, наближений оптимальний розв’язок визначається значеннями R*≈90 галонів, y*≈ 335 галонів.
Отже, оптимальне управління запасами полягає у розміщенні замовлення приблизно на 334 галонів, як тільки запас зменшується до 90 галонів.
Тема7. Ієрархічні моделі прийняття рішень
Приклад
1. Максим
Петренко – випускник-відмінник середньої
школи, що одержав запрошення на навчання
за державний кошт від трьох університетів:
А, В и С. З метою вибору університету
Максим сформулював два основних критерії:
місцезнаходження університету і його
академічна репутація. Будучи відмінним
учнем, він оцінює академічну репутацію
університету в п'ять разів вище, ніж
його місцезнаходження. Далі Максим
використовує системний аналіз для
оцінки трьох університетів з погляду
їхнього місцезнаходження і репутації,
в результаті чого ним отримані такі дві
матриці порівняння:
 ,
,
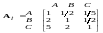 .
.
Необхідно
визначити який з трьох університетів
обере Максим та оцінити узгодженість
матриць порівнянь. Почнемо з головного
ієрархічного рівня, що має справу з
критеріями академічної репутації
університету і його місцезнаходження.
З погляду Максима академічна репутація
університету значно
важливіше його
місцезнаходження. Отже, він приписує
елементові (1,2) матриці А
значення 5, тобто
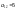 .
Це автоматично означає, що
.
Це автоматично означає, що
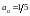 .
Позначивши через Р
і М критерії
репутації університету і його
місцезнаходження, можна записати матрицю
порівняння так.
.
Позначивши через Р
і М критерії
репутації університету і його
місцезнаходження, можна записати матрицю
порівняння так.
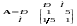 .
.
Відносні
ваги критеріїв Р
і М можуть
бути визначені шляхом ділення елементів
кожного стовпця на суму елементів цього
ж стовпця. Отже, для нормалізації матриці
А
ділимо елементи першого стовпця на
величину 1+1/5=1.2, елементи другого – на
величину 5+1=6. Шукані відносні ваги
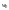 і
і
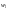 критеріїв
обчислюються тепер у вигляді середніх
значень елементів відповідних рядків
нормалізованої матриці А.
Отже, Середні значення елементів рядків
критеріїв
обчислюються тепер у вигляді середніх
значень елементів відповідних рядків
нормалізованої матриці А.
Отже, Середні значення елементів рядків
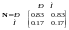
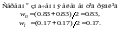
У
результаті обчислень одержали
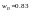 і
і
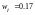 .
Стовпці матриці N
однакові, що має місце лише у випадку,
коли особа, що приймає рішення, виявляє
ідеальну узгодженість
у визначенні
елементів матриці А.
Відносні ваги альтернативних рішень,
що відповідають університетам А, В и С,
обчислюються в межах кожного критерію
Р
і М з
використанням згаданих в умові двох
матриць порівняння.
.
Стовпці матриці N
однакові, що має місце лише у випадку,
коли особа, що приймає рішення, виявляє
ідеальну узгодженість
у визначенні
елементів матриці А.
Відносні ваги альтернативних рішень,
що відповідають університетам А, В и С,
обчислюються в межах кожного критерію
Р
і М з
використанням згаданих в умові двох
матриць порівняння.
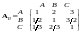
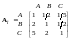 Сума елементів стовпців
Сума елементів стовпців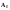 =[1.83, 3.67, 5.5], Сума елементів стовпців
=[1.83, 3.67, 5.5], Сума елементів стовпців
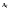 =
[8, 3.5, 1.7]. Елементи матриць
і
визначені
на основі суджень Максима, що стосуються
відносної важливості трьох університетів.
При діленні елементів кожного стовпця
матриць
і
на суму
елементів цих же стовпців одержуємо
наступні нормалізовані матриці.
=
[8, 3.5, 1.7]. Елементи матриць
і
визначені
на основі суджень Максима, що стосуються
відносної важливості трьох університетів.
При діленні елементів кожного стовпця
матриць
і
на суму
елементів цих же стовпців одержуємо
наступні нормалізовані матриці.

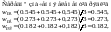
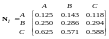

Величини
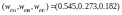 дають відповідні ваги для університетів
А, В и С з точки зору академічної репутації.
Аналогічно величини
дають відповідні ваги для університетів
А, В и С з точки зору академічної репутації.
Аналогічно величини
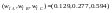 є відносними вагами, що стосуються
місцезнаходження університетів.
Структура задачі прийняття рішень
приведена на рис. 2. Задача має єдиний
ієрархічний рівень із двома критеріями
(місцезнаходження і репутація) і три
альтернативних рішення (університети
А, В и С).
є відносними вагами, що стосуються
місцезнаходження університетів.
Структура задачі прийняття рішень
приведена на рис. 2. Задача має єдиний
ієрархічний рівень із двома критеріями
(місцезнаходження і репутація) і три
альтернативних рішення (університети
А, В и С).
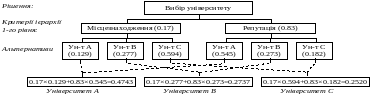 Рис.
2.
Рис.
2.
На
основі цих обчислень університет А
одержує найвищу комбіновану вагу і,
отже, є найбільш оптимальним вибором
Максима. Аналіз матриць порівнянь
свідчить про те, що матриця
є неузгодженою, оскільки стовпці матриці
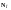 неоднакові. Дослідимо узгодженість
матриці
.
Обчислимо значення
неоднакові. Дослідимо узгодженість
матриці
.
Обчислимо значення
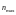 .
З даних прикладу маємо
.
З даних прикладу маємо
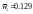 ,
,
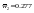 ,
,
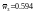 .
Отже,
.
Отже,
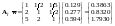 .
Звідси одержуємо
.
Звідси одержуємо
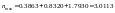 .
Отже, для n=3
маємо
.
Отже, для n=3
маємо
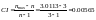 ,
,
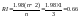 ,
,
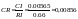 .
Оскільки
.
Оскільки
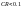 ,
рівень неузгодженості матриці
є прийнятним.
,
рівень неузгодженості матриці
є прийнятним.
