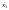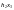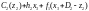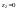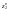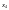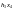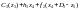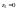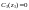- •Тема1. Задача про максимальний потік на мережі
- •Тема2: Сіткові графи
- •Варіанти завдань
- •Тема3. Прийняття рішень в умовах невизначеності та ризик
- •Тема4. Детерміновані моделі управління запасами
- •Тема5. Динамічні моделі управління запасами
- •Тема6. Імовірнісні моделі управління запасами з неперервним контролем рівня запасу
- •Тема7. Ієрархічні моделі прийняття рішень
- •8. Спеціалізовані системи обслуговування з пуассонівським розподілом
Тема5. Динамічні моделі управління запасами
Задача1
Місяць |
Можливості виробництва |
Попит (одиниці) |
|
Звичайний режим роботи, од. |
Понаднормові, од. |
||
1 2 3 4 |
90 100 120 110 |
50 60 80 70 |
100 190 210 160 |
Вартість виробництва одиниці продукції дорівнює 6 доларів в умовах звичайного режиму роботи і 9 доларів при понаднормових роботах. Вартість збереження одиниці продукції протягом місяця дорівнює 0.10 г.о.
Щоб гарантувати допустимість розв’язку при відсутності дефіциту, потрібно, щоб сумарна пропозиція продукції (можливості виробництва) до початку кожного місяця щонайменше дорівнювало сумарному попитові. Про це свідчить наступна таблиця.
Місяць |
Сумарна пропозиція |
Сумарний попит |
1 |
90+50=140 |
100 |
2 |
140+100+60=300 |
100+190=290 |
3 |
300+120+80=500 |
290+210=500 |
4 |
500+110+70=680 |
500+160=660 |
У
табл. 1 подані дані, що відносяться до
розглянутої задачі, і її розв’язку. Тут
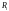 і
і
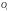 відповідають рівням виробництва у
звичайному і понаднормовому режимі
роботи протягом періоду i,
i=1,2,3,4.
Оскільки сумарна пропозиція в четвертому
періоді перевищує сумарний попит, то
введений фіктивний пункт споживання
(надлишок), щоб збалансувати. Усі
"транспортні" маршрути з попередніх
у поточний період заблоковані, тому що
дефіцит відсутній.
відповідають рівням виробництва у
звичайному і понаднормовому режимі
роботи протягом періоду i,
i=1,2,3,4.
Оскільки сумарна пропозиція в четвертому
періоді перевищує сумарний попит, то
введений фіктивний пункт споживання
(надлишок), щоб збалансувати. Усі
"транспортні" маршрути з попередніх
у поточний період заблоковані, тому що
дефіцит відсутній.
Собівартості
"перевезень" продукції обчислюються
у вигляді суми витрат
на
виробництво
і збереження. Наприклад, відповідна
собівартість від
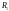 до першого періоду дорівнює лише вартості
виготовлення в 6 г.о., собівартість від
до першого періоду дорівнює лише вартості
виготовлення в 6 г.о., собівартість від
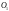 до четвертого періоду – вартості
виготовлення плюс вартість збереження
від першого періоду до четвертого, тобто
9+(0.1+0.1+0.1)=9.30 г.о. Собівартість перевезення
до фіктивного пункту споживання
(надлишок)
дорівнює
нулеві.
до четвертого періоду – вартості
виготовлення плюс вартість збереження
від першого періоду до четвертого, тобто
9+(0.1+0.1+0.1)=9.30 г.о. Собівартість перевезення
до фіктивного пункту споживання
(надлишок)
дорівнює
нулеві.
Таблиця 1.
|
1 |
2 |
3 |
4 |
Надлишок |
|
|||||
R1 |
|
6 |
|
6.1 |
|
6.2 |
|
6.3 |
|
0 |
90 |
90 |
|
|
|
|
|
|
|
|
|
||
O1 |
|
9 |
|
9.1 |
|
9.2 |
|
9.3 |
|
0 |
50 |
10 |
|
30 |
|
10 |
|
|
|
|
|
||
R2 |
|
|
|
6 |
|
6.1 |
|
6.2 |
|
0 |
100 |
|
|
100 |
|
|
|
|
|
|
|
||
O2 |
|
|
|
9 |
|
9.1 |
|
9.2 |
|
0 |
60 |
|
|
60 |
|
|
|
|
|
|
|
||
R3 |
|
|
|
|
|
6 |
|
6.1 |
|
0 |
120 |
|
|
|
|
120 |
|
|
|
|
|
||
O3 |
|
|
|
|
|
9 |
|
9.1 |
|
0 |
80 |
|
|
|
|
80 |
|
|
|
|
|
||
R4 |
|
|
|
|
|
|
|
6 |
|
0 |
110 |
|
|
|
|
|
|
110 |
|
|
|
||
O4 |
|
|
|
|
|
|
|
9 |
|
0 |
70 |
|
|
|
|
|
|
50 |
|
20 |
|
||
|
100 |
190 |
210 |
160 |
20 |
|
|||||
Задача2
Приклад
2. Потрібно
знайти оптимальну стратегію в трьохетапній
системі управління запасами, що
формулюється нижче. Початковий запас
дорівнює
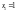 одиниці продукції. Передбачається, що
граничні витрати на придбання продукції
складають 10 г.о за кожну одиницю для
перших трьох одиниць і 20 г.о. – за кожну
додаткову одиницю.
одиниці продукції. Передбачається, що
граничні витрати на придбання продукції
складають 10 г.о за кожну одиницю для
перших трьох одиниць і 20 г.о. – за кожну
додаткову одиницю.
Період i |
Попит Di од. |
Витрати на оформлення замовлення Ki, г.о. |
Витрати на збереження hi г.о. |
1 |
3 |
3 |
1 |
2 |
2 |
7 |
3 |
3 |
4 |
6 |
2 |
Функція виробничих
витрат для періоду i
дорівнює
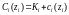 для
для
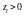 ,
де
,
де
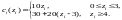
Етап
1.
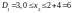 .
.
x2 |
h1x2 |
C1(z1)+h1x2 |
Оптимальний розв’язок |
||||||||
z1=2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
||||
C1(z1)=23 |
33 |
53 |
73 |
93 |
113 |
133 |
f1(x2) |
|
|||
0 |
0 |
23 |
|
|
|
|
|
|
23 |
2 |
|
1 |
1 |
|
34 |
|
|
|
|
|
34 |
3 |
|
2 |
2 |
|
|
55 |
|
|
|
|
55 |
4 |
|
3 |
3 |
|
|
|
76 |
|
|
|
76 |
5 |
|
4 |
4 |
|
|
|
|
97 |
|
|
97 |
6 |
|
5 |
5 |
|
|
|
|
|
118 |
|
118 |
7 |
|
6 |
6 |
|
|
|
|
|
|
139 |
139 |
8 |
|
Оскільки
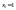 ,
мінімальне значення
,
мінімальне значення
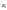 дорівнює
дорівнює
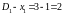 .
.
Етап
2.
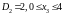 .
.
|
|
|
Оптимальний розв’язок |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
||||
C2(z2)=0 |
17 |
27 |
37 |
57 |
77 |
97 |
f2(x3) |
|
|||
0 |
0 |
0+55=55 |
17+34=51 |
27+23=50 |
|
|
|
|
50 |
2 |
|
1 |
3 |
3+76=79 |
20+55=75 |
30+34=64 |
40+23=63 |
|
|
|
63 |
3 |
|
2 |
6 |
6+97=103 |
23+76=99 |
33+55=88 |
43+34=77 |
63+23=86 |
|
|
77 |
3 |
|
3 |
9 |
9+118=127 |
26+97=123 |
36+76=112 |
46+55=101 |
66+34=100 |
86+23=109 |
|
100 |
4 |
|
4 |
12 |
12+139=151 |
29+118=147 |
39+97=136 |
49+76=125 |
69+55=124 |
89+34=123 |
109+23=132 |
123 |
5 |
|
Етап
3.
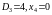 .
.
|
|
|
Оптимальний розв’язок |
|||||
|
1 |
2 |
3 |
4 |
||||
|
16 |
26 |
36 |
56 |
|
|
||
0 |
0 |
0+123=123 |
16+100=116 |
26+77=103 |
36+63=99 |
56+50=106 |
99 |
3 |
Оптимальний
розв’язок визначається наступними
значеннями шуканих змінних:
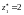 ,
,
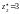 і
і
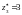 .
При цьому загальні витрати складають
99 г.о.
.
При цьому загальні витрати складають
99 г.о.