
- •Тема1. Задача про максимальний потік на мережі
- •Тема2: Сіткові графи
- •Варіанти завдань
- •Тема3. Прийняття рішень в умовах невизначеності та ризик
- •Тема4. Детерміновані моделі управління запасами
- •Тема5. Динамічні моделі управління запасами
- •Тема6. Імовірнісні моделі управління запасами з неперервним контролем рівня запасу
- •Тема7. Ієрархічні моделі прийняття рішень
- •8. Спеціалізовані системи обслуговування з пуассонівським розподілом
Тема3. Прийняття рішень в умовах невизначеності та ризик
Короткі
теоретичні відомості: Одним з підходів
вирішення задач прийняття рішення в
умовах невизначеності та ризику є
концепція на базі застосування
теоретико-ігрової моделі, згідно з якою
ситуація прийняття рішень характеризується
множиною рішень X
(стратегій) суб’єкта керування, множиною
станів (стратегій)
економічного середовища та матрицею
платежів F:
 .
.
Основними критеріями прийняття рішень в умовах, коли відома інформація про ймовірності появи кожного стану середовища (в умовах ризику) є:
–
критерій Байєса:
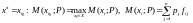 ;
;
–
модальний
критерій:
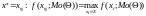 ,
де
,
де
 –мода
випадкової величини;
–мода
випадкової величини;
–
критерій
мінімальної дисперсії:
 ;
;
–
критерій
мінімального коефіцієнта варіації:
 ,
,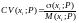 ,
, ;
;
Основними критеріями прийняття рішень у ситуаціях, коли відсутня інформація про ймовірності появи кожного стану середовища чи її не можна застосувати (в умовах невизначеності), є:
–
критерій
Лапласа:
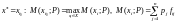 ,
,
 ,
,
 ;
;
–
критерій Вальда:
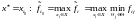 ;
;
–
критерій
мінімального ризику Севіджа:
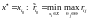 ,
,
 ,
,
 ;
;
–
критерій
Гурвіца:
 ,
,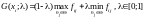 .
.
Тема4. Детерміновані моделі управління запасами
Короткі теоретичні відомості: Природа задачі управління запасами визначається неодноразовим розміщенням і одержанням замовлень заданих обсягів продукції (запасів) у визначені моменти часу.
У
найпростішому випадку з постійним у
часі попитом, миттєвим поповненням
запасу і відсутністю дефіциту сумарні
витрати в одиницю часу можна
представити як функцію від обсяг
замовлення у наступному вигляді
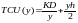 ,
,
де
y – обсяг замовлення, D –
інтенсивність попиту, K – витрати
на оформлення, h – витрати на
збереження. Оптимальна
стратегія управління запасами в даному
випадку формулюється так: замовляти
 одиниць продукції через кожні
одиниць продукції через кожні
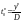 одиниць часу.
одиниць часу.
У
дійсності поповнення запасу не може
відбутися миттєво в момент розміщення
замовлення. Для більшості реальних
ситуацій існує додатній термін
виконання замовлення L (часове
запізнення) від моменту його розміщення
до реального постачання. У цьому випадку
поновлення замовлення має відбуватися
тоді, коли рівень запасу опускається
до LD одиниць. У випадку,
коли термін виконання замовлення L
більший тривалості циклу замовлення
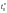 визначається ефективний термін
визначається ефективний термін
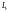 ,
виконання замовлення у вигляді
,
виконання замовлення у вигляді
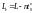 ,
де n – найбільше ціле, що не
перевищує
,
де n – найбільше ціле, що не
перевищує
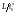 .
Таке рішення пояснюється тим, що після
n циклів (довжиною
кожний) ситуація управління запасами
стає такою ж, як якби інтервал між
розміщенням одного замовлення й
одержанням іншого був рівним
.
Отже, стратегія управління запасами
може бути переформульована таким чином:
замовляти
.
Таке рішення пояснюється тим, що після
n циклів (довжиною
кожний) ситуація управління запасами
стає такою ж, як якби інтервал між
розміщенням одного замовлення й
одержанням іншого був рівним
.
Отже, стратегія управління запасами
може бути переформульована таким чином:
замовляти
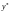 одиниць продукції, як тільки рівень
запасу зменшується до
одиниць продукції, як тільки рівень
запасу зменшується до
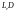 одиниць. У випадку, коли
продукція може бути придбана зі знижкою,
якщо обсяг замовлення y
перевищує деякий фіксований рівень q,
тобто вартість одиниці продукції c
визначається як
одиниць. У випадку, коли
продукція може бути придбана зі знижкою,
якщо обсяг замовлення y
перевищує деякий фіксований рівень q,
тобто вартість одиниці продукції c
визначається як
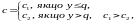
загальні
витрати в одиницю часу можна представити
так

Тоді
визначення оптимального обсягу замовлення
в залежить від того, де знаходиться
точка розриву ціни q стосовно
інтервалів
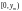 ,
,
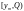 і
і
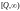 .
Тут
.
Тут
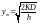 ;
величина
;
величина
 визначається з рівняння
визначається з рівняння
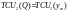 .
Алгоритм визначення оптимального
обсягу замовлення
можна сформулювати в наступному вигляді.
.
Алгоритм визначення оптимального
обсягу замовлення
можна сформулювати в наступному вигляді.
Крок
1. Обчислюємо
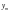 .
Якщо q знаходиться в інтервалі
,
кладемо
.
Якщо q знаходиться в інтервалі
,
кладемо
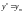 .
У протилежному випадку переходимо до
кроку 2.
.
У протилежному випадку переходимо до
кроку 2.
Крок
2. Знаходимо Q з рівняння
.
Якщо q знаходиться в інтервалі
,
кладемо
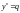 .
Інакше
.
Інакше
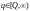 ,
тоді
.
,
тоді
.
У випадку задачі управління запасами n різних товарів, що зберігаються на одному складі обмеженої місткості ці товари можуть конкурувати між собою за обмежений складський простір. При відсутності дефіциту математична модель сформульованої задачі має вигляд:
мінімізувати
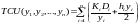
при
обмеженнях 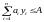 ,
,
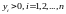 .
.
де
для товару i, i=1,2,...,n використані
такі параметри:
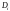 – інтенсивність попиту,
– інтенсивність попиту,
 – вартість розміщення замовлення,
– вартість розміщення замовлення,
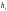 – вартість збереження одиниці товару
в одиницю часу,
– вартість збереження одиниці товару
в одиницю часу,
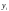 – обсяг замовлення,
– обсяг замовлення,
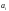 – необхідний простір для збереження
одиниці товару, A – максимальний
складський простір для збереження
товарів n видів. Алгоритм розв’язання
цієї задачі можна описати таким чином.
– необхідний простір для збереження
одиниці товару, A – максимальний
складський простір для збереження
товарів n видів. Алгоритм розв’язання
цієї задачі можна описати таким чином.
Крок 1. Обчислюються оптимальні обсяги замовлень без урахування обмеження за місткістю складу:
 .
.
Крок
2. Здійснюється перевірка, чи
задовольняють знайдені значення
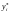 обмеженню за місткістю складу. Якщо
"Так", обчислення закінчуються,
при цьому значення
,
обмеженню за місткістю складу. Якщо
"Так", обчислення закінчуються,
при цьому значення
,
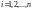 є оптимальними. У протилежному випадку
переходять до кроку 3.
є оптимальними. У протилежному випадку
переходять до кроку 3.
Крок 3. Обмеження за місткістю складу повинно задовольнятися у формі рівності. Для визначення оптимальних обсягів замовлення з урахуванням обмеження будується функція Лагранжа
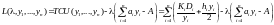 ,
,
де
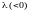 – множник Лагранжа. Необхідні умови
екстремуму функції Лагранжа:
– множник Лагранжа. Необхідні умови
екстремуму функції Лагранжа:
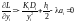 ,
,
 .
.
Постановка задач1: Фарш
TCU(Y)=(KD/Y)+(Yh/2)=((20*300)/300)+(300*(0.03*7)=20*31,5=51,5
K=20г.о; D=300кг; Y=300кг; h=0.03/день=0.21
Y=
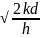 =
=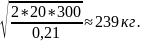
TCU(Y*)=)=(KD/Y*)+(Y*h/2)=((20*300)/239)+(239*0.21/2)=25.1+25,095=50,195
51.5-50.195=1.305г.о
t*=Y*/D=239/300=0.79 тижні ≈ 5.57днів
Постановка задач2: Запаси
Продукція і |
Ki, г.о. |
Di, од. у день |
hi, г.о. |
ai, кв. М |
|
|
|
|||||||
1 |
16 |
11 |
0,3 |
3 |
|
|
|
|||||||
2 |
7 |
6 |
0,3 |
1 |
|
|
|
|||||||
3 |
22 |
7,5 |
0,4 |
4,5 |
|
|
|
|||||||
Загальна площа складу = 35 м2 |
|
|
|
|||||||||||
y1* |
КОРЕНЬ(2*16*11/0.3) |
|
|
|
|
|
|
|||||||
y2* |
КОРЕНЬ(2*7*6/0.3) |
|
|
|
|
|
|
|||||||
y3* |
КОРЕНЬ(2*22*7.5/0.4) |
|
|
|
|
|
|
|||||||
λ= |
-0,26 |
|
|
|
|
|
|
|||||||
y1*= |
КОРЕНЬ(2*16*11/(0.3-2*(-0.26)*3)) |
13,75672 |
||||||||||||
y2*= |
КОРЕНЬ(2*7*6/(0.3-2*(-0.26)*1)) |
10,12122 |
||||||||||||
y3*= |
КОРЕНЬ(2*22*7.5/(0.4-2*(-0.26)*4.5)) |
10,97442 |
||||||||||||
Перевіримо умову місткості складу: |
|
|
34,85 |
13.75+10.12+10.97 |
|
|||||||||
