Закон Кулона

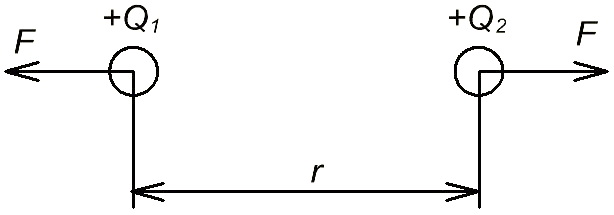
Рисунок 1.3 – Взаимодействие двух зарядов

Сила взаимодействия двух точечных зарядов расположенных в диэлектрической среде прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними, зависит от среды:

где: 1.3

- абсолютная диэлектрическая проницаемость.

1.4

- диэлектрическая проницаемость вакуума (электрическая постоянная)

- относительная диэлектрическая проницаемость – показывает во сколько раз сила взаимодействия в данной среде меньше, чем в вакууме.

1.5

Подставив закон Кулона (1.3) в формулу напряженности (1.2) получим: 1.6

Пример1: Два точечных заряда (Q₁=2*10^-9 Кл, Q₂=4*10^-9 Кл) расположены в среде с относительной диэлектрической проницаемостью =1, на расстоянии 2r друг от друга (r=10 см), определить напряженность электрического поля в точках M и N.

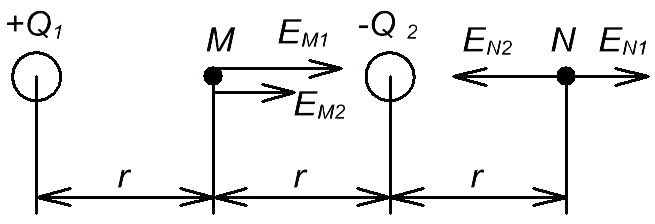
Рисунок 1.4 – Взаимодействие двух зарядов

Для определения напряженности в точке M нужно сложить вектора напряженностей создаваемых первым и вторым зарядом.

Так как вектора и направлены в одну сторону, для получения E_M нужно сложить напряженности E_M1 и E_M2

Для определения напряженности в точке N нужно сложить вектора напряженностей создаваемых первым и вторым зарядом.

Так как вектора и направлены в противоположные стороны, для получения E_N нужно вычесть напряженности E_N1 и E_N2

Пример2: Три точечных заряда (Q₁=Q₂=Q₃=0,6*10^-6 Кл) расположены в среде с относительной диэлектрической проницаемостью =1, в вершинах прямоугольного треугольника, одна сторона которого (r=20 см), α₁=60ْ , α₂=30ْ определить силы действующие на каждый заряд.

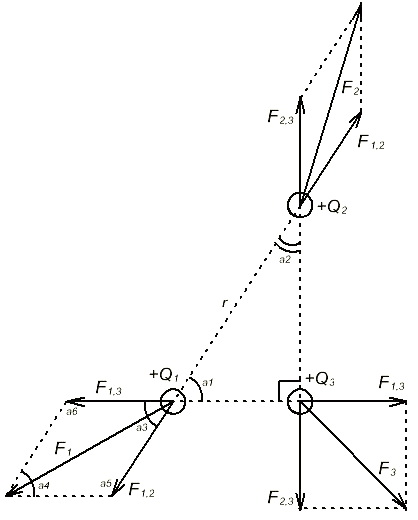
Рисунок 1.5 – Взаимодействие трех зарядов

Для нахождения силы действующей на каждый заряд (F₁, F₂, F₃) нужно найти силы взаимодействия между каждыми двумя зарядами (F_1,2, F_2,3, F_1,3), так как все заряды положительные, то вектора сил взаимодействия будут направлены от зарядов. На каждый заряд будет действовать по две силы. Для их нахождения используем закон Кулона:

Для определения результирующих сил нужно сложить вектора сил, действующих на каждый заряд:

Вектора и расположены под углом α₃ =α₁, для нахождения результирующего вектора достроим вектора до параллелограмма. Угол α₄ будет равен углу α₅, угол α₅ определяется по формуле:

Для определения F₁ воспользуемся теоремой косинусов:

Силы F₂ и F₃ находятся аналогично:

1.2 Потенциал электрического поля. Электрическое напряжение.

Потенциал точки электрического поля это энергетическая характеристика точки поля, величина скалярная, но имеющая знак.

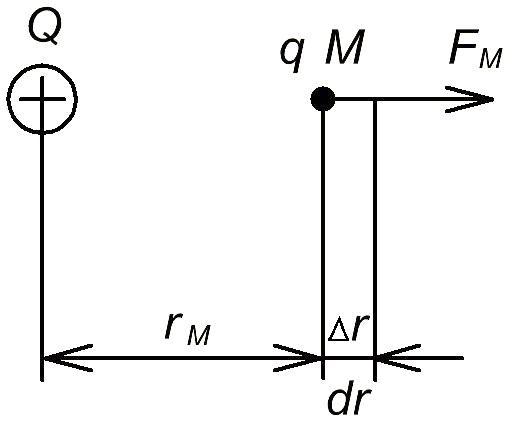
Рисунок 1.6 – Потенциал электрического поля одного заряда

Внесём в точку М поля заряда Q пробный q, увидим что на него действует сила Fм, которая стремится вытолкнуть q из точки М в бесконечность. Если q не закреплён, он начнёт перемещаться под действием этой силы => будет совершаться работа, а это возможно только при наличии энергии => электронное поле в точке M обладает потенциальной энергией. Определим её величину, вычислив совершаемую при этом работу. Чтобы применить эту формулу, необходимо учесть, что F определяется по закону Кулона и зависит от r² между Q и q; а это расстояние всё время меняется, поэтому вычисляем сначала работу на очень малом перемещении, настолько малом, что силу можно считать не изменившейся по величине. На каждом последующем перемещении величина А определяется по такой же формуле, только изменяется расстояние. А отношение этой работы (энергии) к величине неперемещаемого заряда и есть характеристика точки поля, называемого потенциалом.

Потенциал точки электрического поля – это физическая величина, численно равная работе по перемещению единичного заряда из данной точки поля в бесконечность.

Потенциал бесконечно удалённой от заряда точки равен нулю, но нулевой потенциал можно приписать любой точке (как точке отсчёта) в технике за нулевой потенциал принимают потенциал поверхности земли.

Знак потенциала точки определяется знаком заряда поля, вокруг которого этот потенциал определяется.

Если рассматривается поле двух или нескольких точечных зарядов, то потенциал в каждой точке определяется как алгебраическая сумма потенциалов полей каждого из зарядов в отдельности.

Если пробный заряд перемещается из одной точки поля в другую точку поля (из M в N), то совершённая при этом работа определяется

- разность потенциалов двух точек электрического поля называют электрическим напряжением между этими точками – это физическая величина, численно равная работе по перемещению единичного заряда из одной точки поля в другую.

Различие между напряжённостью и напряжением

Е(В/м) напряжённость	U(м) напряжение
Силовая характеристика	Энергетическая характеристика
Векторная величина	Скалярная величина
Относится к одной, каждой точке поля	Относится к двум точкам поля

Связь между E и U устанавливают только для однородного поля