Министерство общего и профессионального образования Свердловской области

ГБОУ СПО СО «Уральский радиотехнический колледж им. А. С. Попова»

Электротехника

Учебное пособие по разделу «Электрические цепи переменного тока»

для студентов специальности 210413, 210414

I часть

2012

Соответствует рабочей программе

специальностей 210413, 210414

УТВЕРЖДЕНО

Цикловой методической комиссией

Радиотехнических дисциплин

Протокол № 13

от «10» мая 2012

Председатель: Е.С. Кравченко

_____________________

Автор: Лебедкин Р.Н.

В данном методическом материале представлен курс лекций по разделу «Электрические цепи переменного тока». Включающий в себя: расчет цепей переменного тока при последовательном, параллельном и смешанном соединении. Символический метод расчета. Трехфазные цепи переменного тока. Расчет цепей с несинусоидальными напряжениями и токами. Нелинейные цепи переменного тока. Переходные процессы в электрических цепях.

Учебное пособие может быть рекомендовано для специальностей 210413,210414 по дисциплине «Электротехника».

Рецензент:

Введение

В структуру атомов и молекул входят элементарные частицы, некоторые из которых обладают электрическим зарядом. Электрический заряд – это важнейшее физическое свойство элементарных частиц, определяющее их силовое взаимодействие.

Любая заряженная частица (заряженное тело) всегда обладает своим электромагнитным полем, которое в зависимости от состояния частицы проявляются одной из своих сторон: либо как электрическое, либо как магнитное.

Электрическое поле (электростатическое) – особый вид материи неразрывно связанный с неподвижной заряженной частицей и оказывающий силовое воздействие на другие неподвижные заряды.

Магнитное поле – особый вид материи неразрывно связанный с подвижной заряженной частице и оказывающий силовое воздействие на другие движущиеся заряды.

Если заряженная частица всегда существует вместе со своим электромагнитным полем, то электромагнитное поле может существовать отдельно от заряженных частиц – в виде электромагнитных волн, существование и распространение которых сопровождается непрерывным преобразованием электрического поля в магнитное и наоборот.

Эти свойства электромагнитного поля являются основой связанных между собой электрических и магнитных явлений – взаимодействие электрически заряженных или намагниченных тел, электрического тока, электромагнитной индукции и т.д.

Использованием этих явлений для получения, передачи и преобразования электрической энергии занимается электротехника.

Раздел 1. Электрические цепи постоянного тока

1. Электрическое поле. Напряженность электрического поля.

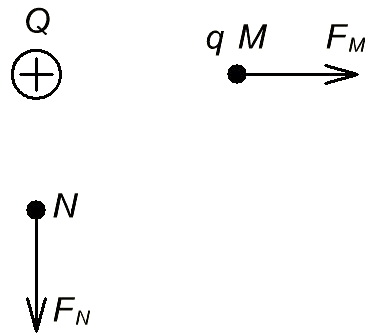
Рисунок 1.1 – Напряженность электрического поля одиночного заряда

Внесем в точку M электрического поля заряда Q, пробный положительный заряд q (Рис 1.1). На заряд q будет действовать сила F_M, стремящаяся вытолкнуть q из точки M в бесконечность (т.к оба заряда положительные). Неоднократно повторяя опыт: внося q в различные точки поля и меняя его величину, можно прийти к выводу, что величина и направление силы действующей на вносимый заряд q зависит от величины q и его положения в поле заряда Q, т.е. от свойств поля в каждой точке.

1.1

Напряженность точки электрического поля (E) – это физическая, векторная величина, численно равная силе действующей на единичный положительный заряд, внесенный в данную точку поля.

Вектор напряженности положительного заряда, всегда направлен от заряда, вектор напряженности отрицательного заряда, всегда направлен к заряду.

Таким образом для определения напряженности можно записать формулу:

1.2

Если рассматривается поле двух или нескольких точечных зарядов, то напряженность в каждой точке такого поля определяется как геометрическая сумма векторов напряженностей полей каждого из зарядов в отдельности.

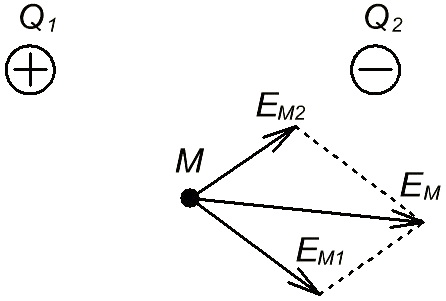
Рисунок 1.2 – Напряженность электрического поля двух зарядов

Величина напряженности определяется для точечных зарядов с помощью формулы выведенной на основании закона Кулона, а для объемных заряженных тел с помощью формул выведенных на основании теоремы Остроградского – Гаусса.