4. Оценка качества регулирования
По таблице 6 строим вещественно-частотную характеристику замкнутой системы регулирования (рисунок 7).
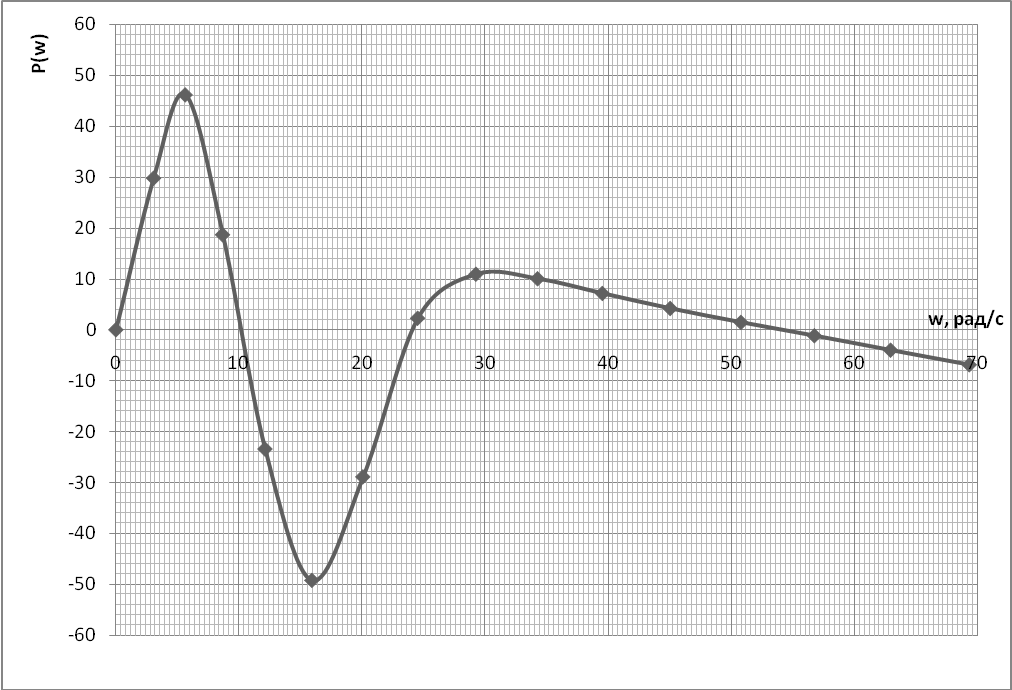
Рисунок 7. Вещественно-частотная характеристика замкнутой системы регулирования
Будем рассматривать только первые 2 колебания. Вещественно-частотная характеристика (рис.7), разбивается на ряд трапеций. В данном случае их получилось четыре. Характеристики трапеций представлены в таблице 7.
Вещественно – частотную характеристику заменим трапециями (рис. 8)
Рисунок 8. Вещественно – частотная характеристика замкнутой системы регулирования
Таблица 8. Характеристики трапеций.
№ трап. |
Р |
ωp |
ωn |
ωp/ωn = χ |
1 |
46,21 |
5,629 |
10,05 |
0,56 |
2 |
-46,21 |
0 |
5,629 |
0 |
3 |
-49,29 |
15,922 |
23,5 |
0,677 |
4 |
49,29 |
10 |
15,922 |
0,628 |
5. Построение переходного процесса
График переходного процесса φΣ(t) = φ1(t) - φ2(t) - φ3(t) + φ4(t),
где φ1(t), φ2(t), φ3(t), φ4(t) – составляющие переходного процесса, которые определяются по h-функции для каждой трапеции. h(x) берется из [3, стр. 56-57].
Коэффициент наклона трапеции:
φi(t) = hi(x) *Vi(x),
где i = 1,2,3,4.
Размерное время:
t = τ/ωп
По полученным данным строим график составляющих переходного процесса φ1(t), φ2(t), …,φ4(t), которые затем графически складываются (рисунок 9).
Рисунок 9. Составляющие φi(t) и кривая переходного процесса φ∑(t).
Суммарный график φ∑(t) характеризует переходный процесс автоматического регулирования при единичном скачкообразном возмущении.
Таблица 9. Данные для построения кривой переходного процесса.
Фсумм |
t,с |
хвых(t) |
0 |
0 |
0 |
7,5 |
0,1 |
45 |
23 |
0,2 |
138 |
36,5 |
0,3 |
219 |
24 |
0,4 |
144 |
15 |
0,5 |
90 |
12 |
0,6 |
72 |
7 |
0,7 |
42 |
4 |
0,8 |
24 |
2 |
0,9 |
12 |
3,5 |
1 |
21 |
4 |
1,1 |
24 |
4 |
1,2 |
24 |
4,5 |
1,3 |
27 |
4 |
1,4 |
24 |
3 |
1,5 |
18 |
1,5 |
1,7 |
9 |
0,5 |
1,9 |
3 |
0,5 |
2,1 |
3 |
Поскольку величина возмущения на входе системы была равна 6, ординаты суммарной кривой переходного процесса пересчитываем с учетом данной величины.
На рисунке 10 приведена кривая переходного процесса, построенная с учетом величины входного возмущения.
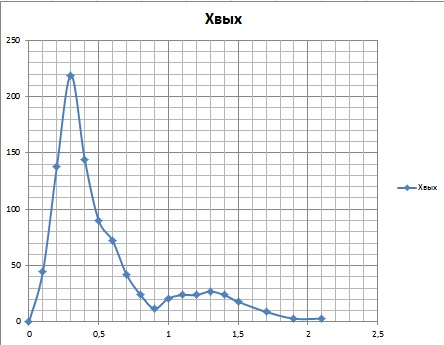
Рисунок 10. Кривая переходного процесса.
Ранее с помощью программ расчета кривой переходного процесса в системе с ПИД-регулятором был построен график переходного процесса, и этот график совпадает с кривой, рассчитанной вручную.
СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА ПОКАЗАТЕЛЕЙ РЕГУЛИРОВАНИЯ
С помощью графика переходного процесса (рис. 10) определим
Х1* - максимальное динамическое отклонение
τр* - время регулирования
η – степень перерегулирования
Таблица 10 – Сравнение расчетных и заданных значений.
Показатели |
Х1 |
∆Хст |
τр |
η |
Предельные значения |
360 |
120 |
3,0 |
5 |
Полученные значения |
219 |
- |
1,8 |
0 |
Вывод: сравнение расчетных и заданных параметров показывает, что система автоматического регулирования удовлетворяет показателям качества.