2.2 Определение параметров настройки регулятора
Передаточная функция:
Определяем настройки ПИД-регулятора:
;
.
с;
с.
2.3 Анализ работы системы с пид-регулятором
РАСЧЕТ ПАРАМЕТРИЧЕСКОЙ ОБЛАСТИ УСТОЙЧИВОСТИ СИСТЕМЫ
Область устойчивости – зависимость, отражающая допустимые пределы изменений параметров настройки регулятора, при которых конкретная система остается устойчивой.
Расчет произведен с помощью компьютерных программ.
Результаты расчета параметрической области устойчивости системы с ПИД-регулятором представлены в таблице 3 и на рисунке 1.
Таблица 3. Область устойчивости.
Время изодрома Тиз, с |
Критическое значение К(р) |
0,048 |
0,0049 |
0,096 |
0,00373 |
0,143 |
0,0436 |
0,191 |
0,0429 |
0,239 |
0,0423 |
0,287 |
0,0418 |
0,335 |
0,0415 |
0,384 |
0,0412 |
0,432 |
0,0410 |
0,480 |
0,0408 |
По данным таблицы 3 строим график, на котором определяем рабочую точку (рисунок 1).
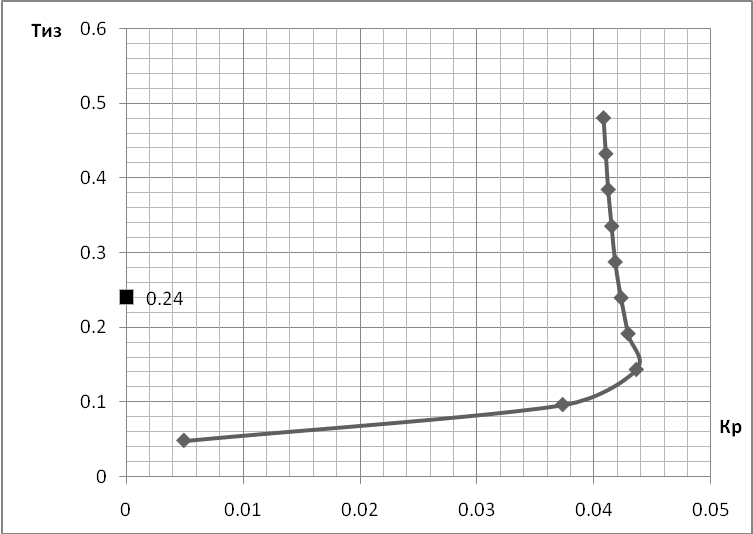
Рисунок 1. Область устойчивости системы с ПИД-регулятором.
Координаты рабочей точки (0; 0,240).Система является устойчивой.
Рассчитываем переходный процесс.
Таблица 4. Переходный процесс.
Т, с |
Х(Т) |
0 |
0 |
0,264 |
246,94 |
0,356 |
181,3680 |
0,712 |
21,9108 |
1,068 |
-0,3893 |
1,156 |
-0,85 |
1,424 |
-0,3633 |
1,780 |
-0,0306 |
2,136 |
0,0023 |
2,492 |
0,0005 |
2,848 |
0,0002 |
3,204 |
0,0002 |
3,560 |
0,0002 |
3,916 |
0,0002 |
По полученным данным строим график переходного процесса (рисунок 2).
t1 = 0,270; x1 = 254
t2 = 1,156; x2 = -0,85
Параметрами переходного процесса являются :
1) амплитуда колебаний (х1 ,х2),
2)η = (х2/х1)*100%,
3) время регулирования
Таблица 5. Параметры переходного процесса.
Параметр |
Заданное значение |
Расчетное значение |
х1 |
360 |
254 |
η |
5 |
0,33 |
∆Хст |
120 |
0 |
τр |
3,0 |
0,9 |
Рисунок 2. Кривая переходного процесса в системе с ПИД-регулятором.
Вывод: САР с ПИД – регулятором подходит, так как рассчитанные параметры удовлетворяют заданным условиям: η < η (зад); τр< τр (зад). Система устойчива и удовлетворяет показателям качества.
3. Анализ частотных характеристик проектируемой системы
Таблица 6. Результаты расчета частотных характеристик.
частота, рад/с |
АФХ |
|||||||
объекта |
регулятора |
разомкнутая |
замкнутая |
|||||
А(об) |
Ф(об) |
А(р) |
Ф(р) |
А |
Ф |
вещ |
мним |
|
0 |
150 |
0 |
max |
-90 |
max |
-90 |
0 |
0.000 |
3.064 |
94.83 |
-72 |
0.0331 |
-46 |
3.14 |
-118 |
29.83 |
15.657 |
5.629 |
60.88 |
-105 |
0.0246 |
-20 |
1.49 |
-125 |
46.21 |
-17.912 |
8.667 |
41.57 |
-134 |
0.023 |
0 |
0.96 |
-134 |
18.71 |
-50.549 |
12.112 |
30.32 |
-162 |
0.0239 |
16 |
0.72 |
-146 |
-23.44 |
-47.697 |
15.922 |
23.27 |
-191 |
0.0261 |
28 |
0.61 |
-162 |
-49.29 |
-11.441 |
20.064 |
18.55 |
-221 |
0.0292 |
38 |
0.54 |
-183 |
-28.93 |
28.113 |
24.513 |
15.22 |
-253 |
0.033 |
46 |
0.5 |
-207 |
2.27 |
25.384 |
29.25 |
12.77 |
-286 |
0.0374 |
52 |
0.48 |
-234 |
10.94 |
11.135 |
34.258 |
10.92 |
-321 |
0.0422 |
57 |
0.46 |
-264 |
10.04 |
2.311 |
39.523 |
9.47 |
-358 |
0.0475 |
61 |
0.45 |
-297 |
7.15 |
-2.120 |
45.033 |
8.31 |
-396 |
0.0531 |
64 |
0.44 |
-332 |
4.19 |
-4.177 |
50.778 |
7.38 |
-436 |
0.0591 |
67 |
0.44 |
-369 |
1.46 |
-4.940 |
56.748 |
6.6 |
-478 |
0.0654 |
69 |
0.43 |
-408 |
-1.17 |
-4.835 |
62.936 |
5.95 |
-520 |
0.0719 |
71 |
0.43 |
-449 |
-4.01 |
-3.682 |
69.333 |
5.41 |
-565 |
0.0788 |
73 |
0.43 |
-492 |
-6.89 |
0.090 |
Таблица 7. Амплитудно –фазовые характеристики.
частотарад/с |
АФХ |
|||||||
объекта |
регулятора |
разомкнутая |
замкнутая |
|||||
вещ |
мним |
вещ |
мним |
вещ |
мним |
вещ |
мним |
|
0 |
150 |
0 |
|
|
|
|
0 |
0.000 |
3.064 |
29.3041 |
-90.1887 |
0.022993 |
-0.02381 |
-1.47414 |
-2.77246 |
29.83 |
15.657 |
5.629 |
-15.7569 |
-58.8056 |
0.023116 |
-0.00841 |
-0.85463 |
-1.22054 |
46.21 |
-17.912 |
8.667 |
-28.8769 |
-29.903 |
0.023 |
0 |
-0.66687 |
-0.69057 |
18.71 |
-50.549 |
12.112 |
-28.836 |
-9.3694 |
0.022974 |
0.006588 |
-0.59691 |
-0.40262 |
-23.44 |
-47.697 |
15.922 |
-22.8425 |
4.44013 |
0.023045 |
0.012253 |
-0.58014 |
-0.1885 |
-49.29 |
-11.441 |
20.064 |
-13.9999 |
12.1699 |
0.02301 |
0.017977 |
-0.53926 |
0.02826 |
-28.93 |
28.113 |
24.513 |
-4.4499 |
14.555 |
0.022924 |
0.023738 |
-0.4455 |
0.22699 |
2.27 |
25.384 |
29.25 |
3.51989 |
12.2753 |
0.023026 |
0.029472 |
-0.28214 |
0.38833 |
10.94 |
11.135 |
34.258 |
8.48643 |
6.87218 |
0.022984 |
0.035392 |
-0.04808 |
0.45748 |
10.04 |
2.311 |
39.523 |
9.46423 |
0.3305 |
0.023028 |
0.041544 |
0.204296 |
0.40095 |
7.15 |
-2.120 |
45.033 |
6.72293 |
-4.8845 |
0.023278 |
0.047726 |
0.388497 |
0.20656 |
4.19 |
-4.177 |
50.778 |
1.78538 |
-7.16078 |
0.023092 |
0.054402 |
0.434583 |
-0.0688 |
1.46 |
-4.940 |
56.748 |
-3.09851 |
-5.82745 |
0.023437 |
0.061056 |
0.287726 |
-0.3196 |
-1.17 |
-4.835 |
62.936 |
-5.59117 |
-2.03502 |
0.023408 |
0.067983 |
0.007505 |
-0.42993 |
-4.01 |
-3.682 |
69.333 |
-4.90313 |
2.28636 |
0.023039 |
0.075357 |
-0,260961 |
-0.31955 |
-6.89 |
0.090 |
Re = A*cos(рад(Ф))
Im = A*sin(рад(Ф))
На основании данных таблицы 7 строим амплитудно-фазо–частотные характеристики объекта, регулятора, разомкнутой и замкнутой системы.
Рисунок 3 – Амплитудно-фазовая частотная характеристика объекта
Рисунок 4 – Амплитудно-фазовая частотная характеристика регулятора
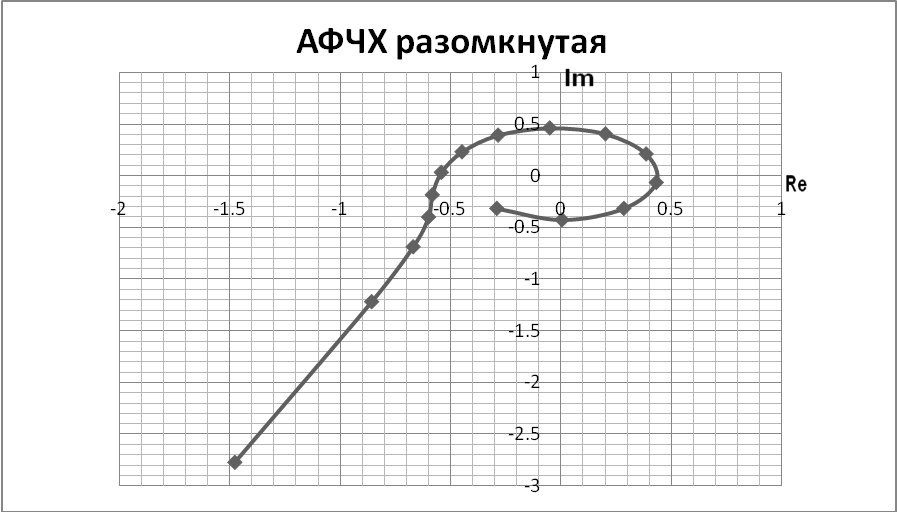
Рисунок 5. Амплитудно-фазовая частотная характеристика разомкнутой системы автоматического регулирования
Годограф амплитудно-фазовой частотной характеристики разомкнутой системы (рисунок 5) используется для оценки устойчивости системы с помощью критерия Найквиста. Данная система является устойчивой, поскольку годограф разомкнутой системы при изменении ω от 0 до ∞ не охватывает на комплексной плоскости критическую точку с координатами (–1; 0). На основании этого делаем вывод о том, что замкнутая система также будет устойчивой.
По расположению годографа на плоскости комплексного переменного определяются коэффициенты запаса устойчивости анализируемой системы по модулю m и по фазе γ.
В данной системе запасы устойчивости:
m = 0,45;
γ = 46°.
Рисунок 6. Амплитудно-фазовая частотная характеристика замкнутой системы автоматического регулирования
Разомкнутая система является устойчивой. На основании этого делаем вывод о том, что замкнутая система также будет устойчивой.