11. Задача составления смесей

Несмотря на то что оба рассмотренных примера — Oak Product и транспортная мо­дель — оказались моделями максимизации, многие реальные задачи сводятся к задачам минимизации. Когда целью является прибыль, ее необходимо максимизировать, но если цель — уменьшить затраты, то приходим к задаче минимизации. В качестве модели ми­нимизации рассмотрим следующий пример.

При создании сплава для новой продукции компании Eastern Steel используется же­лезная руда, получаемая с четырех различных шахт. Как показал анализ, чтобы получить сплав с нужными свойствами, необходимо удовлетворить минимальные требования по трем основным элементам, которые для простоты обозначили А, В и С. В частности, ка­ждая тонна руды должна содержать не менее 5 фунтов элемента А, 100 фунтов элемента В и 30 фунтов элемента С. Эти данные приведены в табл. 6.

Таблица 6. Требования к содержанию основных элементов

Элемент	Минимальное содержание, фунт/т
А	5
Р.	100
С	30

Руда с каждой шахты содержит все три основных элемента, но в разных количествах. Состав руды (содержание элементов) приведен в табл. 7.

Таблица 7. Состав руды с различных шахт

		Шахта (содержание	элементов, фунт/т)
Элемент	I	2	3	4
А	10	3	8	2
В	90	150	75	175
С	45	25	20	37

Заметим, что тонна руды с первой шахты содержит 10 фунтов элемента А и, следова­тельно, удовлетворяет минимальному требованию к содержанию данного элемента (5 фунтов в тонне). Кроме того, она содержит 90 фунтов элемента В и 45 фунтов элемен­та С, таким образом требование к содержанию элемента С удовлетворяется, а к содержа­нию элемента В — нет. Аналогично тонна руды со второй шахты не удовлетворяет требо­ваниям к содержанию элементов А и С, тонна руды с третьей шахты — требованиям к содержанию В и С, а с четвертой — требованию к содержанию А. Однако можно соста­вить разнообразные смеси (в которых в различных пропорциях будут смешиваться руды с разных шахт), удовлетворяющие минимальным требованиям по всем основным эле­ментам. Пример такой смеси: 1/2 тонны руды с шахты 1 и 1/2 тонны руды с шахты 4. Со­держание элемента А в тонне такой смеси вычисляется по формуле:

содержание А = (1/2)х(содержание А в тонне руды с шахты 1) + + (1/2)х(содержание А в тонне руды с шахты 4).

Таким образом, содержание элемента А = (1/2)х 10 +(1/2)х2 = 5+1=6.

Поскольку 6>5, требование по минимальному содержанию элемента А удовлетворено.

Аналогично можно рассчитать содержание элемента В в тонне смеси:

содержание В = (1/2)х(содержание В в тонне руды с шахты 1) + < 1/2)х (содержание В в тонне руды с шахты 4).

Следовательно, содержание элемента В = (1/2)х90 + (1/2)х175 = 132,5. Наконец, содер­жание элемента С в тонне смеси равно (1/2)х45 + (1/2)х37 = 41.

Сравнивая полученные значения с требуемым содержанием В (100 фунтов) и С (30 фунтов), видим, что данная смесь (1/2 тонны с шахты 1 и 1/2 тонны с шахты 4) удов­летворяет всем требованиям по минимальному содержанию элементов, следовательно, она является допустимой смесью. Существует много других смесей, которые также удов­летворяют всем требованиям и являются допустимыми. Однако, поскольку руда с разных шахт имеет различную стоимость, стоимость смесей также различается. Стоимостные данные содержатся в табл. 8.

Таблица 8. Стоимость руды с различных шахт

Шахта Стоимость тонны руды, $

1. 800

1. 400

1. 600

1. 500

Например, стоимость допустимой смеси, тонна которой состоит из половины тонны руды с шахты 1 и половины тонны руды с шахты 4, вычисляется по формуле:

(1/2)х(стоимость тонны руды шахты 1) + (1/2)х(стоимость тонны руды шахты 4) =

= (1/2)х800 + (1/2)х500 = $650.

Можно попробовать сравнить эту стоимость со стоимостью других допустимых сме­сей. Цель компании Eastern Steel — найти самую дешевую допустимую смесь. Сформули­руем данную задачу в виде модели линейного программирования.

Поскольку нужно найти оптимальный состав одной тонны смеси, зададим перемен­ные решения следующим образом:

Т₁ — часть тонны, состоящая из руды с шахты 1,

Т₂ — часть тонны, состоящая из руды с шахты 2,

Т₃ — часть тонны, состоящая из руды с шахты 3,

Т₄ — часть тонны, состоящая из руды с шахты 4.

С помощью данных табл. 7 вычислим количества основных элементов в одной тон­не смеси:

количество элемента А в 1 т смеси =10 Т₁ +3 Т₂ +8 Т₃ +2 Т₄ (9)

количество элемента В в 1 т смеси =90 Т₁ + 150 Т₂ + 75Т₃+175 Т₄ (10)

количество элемента С в 1 т смеси = 45Т₁ + 25Т₂ + 20Т₃ + 37Т₄ (11)

Теперь скомбинируем выражения (9), (10) и (11) с требованиями по минималь­ному содержанию элементов, приведенными в табл. 4, и получим три ограничения.

10 Т₁ +3 Т₂ +8 Т₃ +2 Т₄ >=5, (12)

90 Т₁ + 150 Т₂ + 75Т₃+175 Т₄ >= 100, (13)

45Т₁ + 25Т₂ + 20Т₃ + 37Т₄ >=30. (14)

Существуют ли в данной модели другие ограничения? Необходимо включить условия неотрицательности переменных решения Т₁, Т₂ , Т₃, Т₄, однако есть еще одно важное ог­раничение. Поскольку тонна смеси состоит только из руды указанных четырех шахт, сумма составляющих смеси должна быть равна 1:

Т₁ + Т₂ + Т₃ + Т₄ = 1. (15)

Последнее ограничение иногда называют условием материального баланса и ограниче­нием в виде равенства. Оно ограничивает значения переменных решения таким образом, что левая часть в точности равна правой части.

Ограничения модели линейного программирования могут быть как равенствами, так и неравенствами.

Используя данные табл. 8, легко получить формулу для вычисления стоимости тон­ны любой смеси:

стоимость 1 т смеси = 800 Т₁ + 400 Т₂ + 600 Т₃ + 500 Т₄ .

Теперь можем составить полную символическую модель.

Минимизировать 800 Т₁ + 400 Т₂ + 600 Т₃ + 500 Т₄

при ограничениях

10 Т₁ +3 Т₂ +8 Т₃ +2 Т₄ >=5,

90 Т₁ + 150 Т₂ + 75Т₃+175 Т₄ >= 100,

45Т₁ + 25Т₂ + 20Т₃ + 37Т₄ >=30,

Т₁ + Т₂ + Т₃ + Т₄ = 1,

Т₁, Т₂, Т₃, Т₄ >==0.

Все функции модели являются линейными, следовательно, это модель линейного программирования.

Табличное представление модели, ее оптимальное решение, диалого­вое окно Поиск решения, а также формулы представлены на рис. 25.

Рис. 25. Модель составления рудной смеси

12. Создание моделей ЛП

Чтобы попрактиковаться в формировании моделей, постарайтесь самостоятельно по­строить модели для следующих задач. Ознакомившись с исходными данными, старайтесь сразу же разработать символическую модель ЛП. На данном этапе не следует использо­вать дополнительные ограничения, логические нюансы или полет фантазии, которые могут, на ваш взгляд, сделать модель более реалистичной. Не нужно думать о том, что случится на будущей неделе, если в задаче речь о следующей неделе не идет. Предлагае­мые задачи должны помочь вам научиться формулировать модели при условии, что этап перехода от реальной ситуации к абстракции уже выполнен. Чтобы вы могли проверить результаты своей работы, необходима однозначная формулировка задачи. Иными слова­ми, в отличие от реальных ситуаций, здесь для каждой задачи существует правильный от­вет. Позднее, когда у вас будет больше опыта, можно будет вносить в модели дополни­тельные штрихи и нюансы реальной жизни.

Пример 1. Задача об ассортименте продукции

Компания производит две марки телевизоров — Astro и Cosmo. Работают два конвей­ера, каждый из которых выпускает телевизоры одной марки, и два цеха, занятых произ­водством деталей для телевизоров обеих марок. Производственная мощность конвейера, выпускающего Astro, составляет 70 телевизоров в день, а конвейера Cosmo — 50 телеви­зоров вдень. Цех А производит телевизионные трубки. На производство трубки для теле­визора Astro требуется I ч рабочего времени, а на производство трубки для Cosmo — 2 ч. На данном этапе в цеху А производству трубок для телевизоров обеих марок может быть уделено не более 120 ч рабочего времени в день. В цеху Б изготавливаются корпуса теле­визоров, причем на производство одного корпуса как для Astro, так и для Cosmo требует­ся I ч рабочего времени. Цех Б может посвятить изготовлению корпусов не более 90 ч ра­бочего времени вдень. Удельная валовая прибыль от реализации Astro и Cosmo составля­ет 20 и 10 долларов соответственно. Эти данные представлены в табл. 9.

Таблица 9. Данные о производстве телевизоров

		Удельные трудозатраты, ч
	Дневная производительность	Цех А	Цех Б	Удельная прибыль,
Astro	70	1	1	20
Cosmo	50	2	1	10

Ресурс рабо- 120 90

чего времени

При условии, что компания может продать все произведенные телевизоры, каким должен быть дневной план производства (т.е. сколько телевизоров каждой марки следует производить ежедневно)?

Символическая модель ЛП для данной задачи имеет следующий вид.

А — дневной выпуск телевизоров Astro (штук/день).

С — дневной выпуск телевизоров Cosmo (штук/день).

Максимизировать 20А + 10С

при ограничениях

А<=70,

С<=50,

А + 2С<= 120,

А + С<=90,

А,С>=0.

Заметим, что, как и в модели Oak Product, в некоторые ограничения входят не все пе­ременные решения. Например, переменная С не входит в первое ограничение (А<=70). В общем случае не обязательно, чтобы все переменные решения входили в каждое огра­ничение. Табличная модель Excel для данной задачи с оптимальными решениями, а так­же диалоговое окно Поиск решения представлены на рис. 26. Формулы для вычисле­ния прибыли и суммарных значений в левых частях неравенств аналогичны соответст­вующим формулам модели составления рудной смеси, поэтому здесь и в последующих примерах мы их не приводим. Для ограничения по трудозатратам в цеху Б и для ограни­чения производственной мощности по выпуску телевизоров Astro резерв оказался не в точности равен нулю. Такая ситуация достаточно типична: во многих решениях, пред­лагаемых средством Поиск решения, резерв может принимать очень маленькие положи­тельные или отрицательные значения, поскольку программа имеет ограниченную точ­ность вычислений. Эти малые значения отражают предел вычислительной точности Ex­cel и на практике могут считаться равными 0.

Рис. 26. Модель задачи об ассортименте продукции

Пример 2. Задача составления смеси

Жестяная банка корма для собак весом 16 унций должна содержать как минимум сле­дующие количества питательных веществ: белков — 3 унции, углеводов — 5 унций и жи­ров— 4 унции. Нужно смешать четыре вида каш в различных пропорциях, чтобы полу­чить наиболее дешевую банку собачьего корма, удовлетворяющую требованиям по со­держанию питательных веществ. Содержание питательных веществ и цена каждой каши в расчете на 16 унций приводятся в табл. 10.

Таблица 10. Данные о цене и содержании питательных веществ

		Содержание питательных веществ и цена
Каша	Содержание белков,	Содержание углеводов,	Содержание жиров,	Цена, долл.
	унции	унции	унции
1	3	7	5	4
2	5	4	6	6
3	2	2	6	3
4	3	8	2	2

Модель линейного программирования для задачи по составлению корма для собак имеет следующий вид.

Минимизировать

4х₁ + 6х₂ + Зх₃ + 2х₄

при ограничениях

Зх₁+ 5 х₂+ 2х₃ + З х₄ >= 3,

7х₁+ 4 х₂ + 2х₃+ 8 х₄ >= 5,

5х₁+ 6 х₂ + 6x₃ + 2x₄>=4,

х₁ + х₂ + х₃ + х₄ = 1,

х₁, х₂, х₃, х₄ >= 0.

Табличное представление модели, оптимальное решение, а также параметры для средства Поиск решения показаны на рис. 27.

Рис. 27. Модель задачи по составлению оптимального корма для собак

Заметим, что в предыдущем примере дробные значения переменных решения могут считаться недопустимыми (если не предполагать, что они представляют средний еже­дневный выпуск). А в этом примере дробные значения естественны и допустимы.

Пример 3. Составление расписания

Управляющий персоналом университета должен составить расписание охраны терри­тории университета, удовлетворяющее требованиям, представленным в табл. 11.

Таблица 11. Требования к организации охраны территории

Время Минимальное число офицеров охраны

0.00-4.00 5

4.00-8.00 7

8.00-12.00 15

12.00-16.00 7

16.00-20.00 12

20.00-24.00 9

Офицеры дежурят посменно, продолжительность смены 8 ч. На каждый день уста­новлено 6 смен. Время начала и конца каждой смены показано в табл. 12.

Таблица 12. Расписание смен

Смена Время начала Время окончания

1. 0.00 8.00

1. 4.00 12.00

1. 8.00 16.00

1. 12.00 20.00

1. 16.00 24.00

1. 20.00 4.00

Управляющий персоналом хочет определить, сколько офицеров назначить в каждую смену, чтобы минимизировать их количество и при этом удовлетворить требования к организации охраны. Переменные решения можно определить следующим образом.

Х₁ — число офицеров, дежурящих в смену I;

X₂ — число офицеров, дежурящих в смену 2;

Х₆ — число офицеров, дежурящих в смену 6.

Целевая функция имеет вид Х₁+ Х₂ + Х₃ + Х₄ + X₅ + Х₆. При формулировке ограниче­ний нужно убедиться, что определенный набор значений переменных Х₁ ..., Х_ь удовле­творяет требованиям по организации охраны территории. Нужно выбрать некий меха­низм, который позволит определить, какие офицеры находятся на дежурстве в течение каждого из указанных в требованиях интервалов времени. В этом может помочь табл. 13. Так, офицеры, дежурящие в первую смену, находятся на посту в течение пер­вых двух временных интервалов и т.д. С помощью таблицы также можно определить (суммируя значения в одном столбце), сколько офицеров находится на дежурстве в тече­ние каждого временного интервала (например, в первый интервал дежурит x1+ x6 офи­церов; поэтому первое ограничение выглядит следующим образом: x1+ x6 >= 5).

Таблица 1 Количество офицеров, дежурящих в течение каждого временного интервала

Временной интервал

Смена 0.00-4.00 4.00-8.00 8.00-12.00 12.00-16.00 16.00-20.00 20.00-24.00

1 x1 x1

2 x2 x2

3 x3 x3

4 x4 x4

5 x5 x5

6 x6 x6

Надо 5 7 15 7 12 9

Символическая модель имеет следующий вид.

Минимизировать Х₁+ Х₂ + Х₃ + Х₄ + X₅ + Х₆.

при ограничениях

Х₁+ Х₆ >=5,

Х₁+ Х₂ >=7,

Х₂+ Х₃ >=15,

Х₃+ Х₄ >=7,

Х₄+ Х₅ >=12,

Х₅+ Х₆>=9,

Х_i >=0, i= 1,2,..., 6.

Данная задача является еще одним примером, в котором переменные решения долж­ны принимать целочисленные значения. Табличная модель с оптимальными решениями, а также параметры для средства Поиск решения представлены на рис. 28.

Задачи такого типа использовались при составлении расписания дежурств операторов телефонных станций. Как правило, каждый час разбивается на 15-минутные интервалы; в сутках 24 часа, следовательно, имеется 94 ограничения. Количество переменных реше­ния определяется тем, сколько существует возможных смен.

Рис. 28. Модель задачи по составлению расписания дежурств

Пример 4. Анализ безубыточности при наличии ограничений

Компания Longer Boats производит три вида высококлассных гоночных яхт — Sting, Ray и Breaker. Соответствующие данные о затратах и доходах на ближайший плановый период представлены в табл. 14.

Таблица 14. Данные о затратах и доходах компании Longer Boats

Яхты	Цена, долл. за единицу	Переменные затраты, за единицу	Фиксиров. затраты
Sting	10 000	5 000	5 000 000
Ray	7 500	3 600	3 000 000
Breaker	15 000	8 000	10 000 000

Как свидетельствуют эти данные, фиксированные затраты в каждом случае весьма значительные. Фиксированные затраты — это всевозможные расходы, которые сущест­вуют независимо от того, какое количество продукта производится. Так, для яхт класса Ray потребуется затратить те же самые S3 000 000 независимо от того, будет построена 1 яхта этого класса, 40 яхт или 0. Высокие фиксированные затраты включают в себя за­траты на модификацию проекта, создание макета и испытание яхты в бассейне.

На рис. 25 представлено определение точки безубыточности (критического объема производства) для яхт класса Sting. Как следует из графика, если компания Longer Boats будет производить только яхты Sting, то для того, чтобы добиться безубыточности, ей по­требуется выпустить не менее 1 000 яхт.

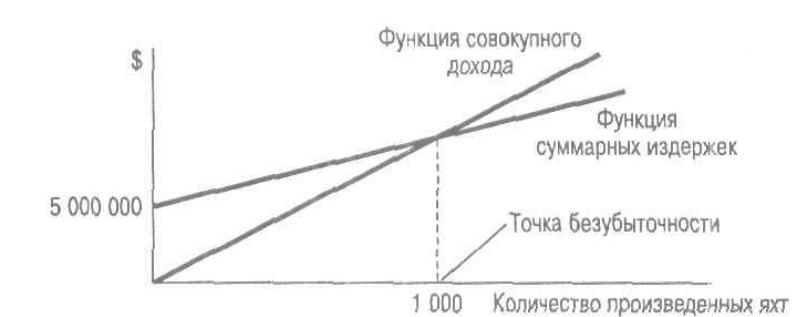Рис. 25. Анализ безубыточности для производства яхт Sting

Однако перед компанией Longer Boats стоит более сложная задача. Во-первых, на следующий плановый период руководство компании уже заключило контракт на произ­водство 700 яхт Sting. Во-вторых, еще один клиент заказал 400 яхт Breaker, и руководство заинтересовано в выполнении данного заказа. В-третьих, анализ рынка, проведенный отделом маркетинга компании, свидетельствует, что следует произвести не более 300 яхт Ray. Руководство компании хочет выяснить, сколько каких яхт необходимо продать, что­бы добиться безубыточности. Таким образом, необходимо учесть наличие трех моделей, а также заключенных соглашений.

Начнем с общих положений: точка безубыточности характеризуется тем, что суммар­ный доход равняется суммарным затратам. Поскольку компания Longer Boats создана относительно недавно и испытывает определенные сложности с платежами (что связано с быстрым ростом компании), руководство заинтересовано в том, чтобы минимизиро­вать расходы. Поскольку фиксированные затраты придется нести в любом случае, целью можно считать минимизацию суммарных переменных затрат. Таким образом, поставлена задача найти производственный план с наименьшими переменными затратами, соответ­ствующий ограничениям и приносящий доход, равный суммарным затратам.

Чтобы получить уравнение точки безубыточности в зависимости от количества про­изведенных яхт определим переменные решения следующим образом.

S — количество произведенных яхт класса Sting,

R — количество произведенных яхт Ray,

В — количество произведенных яхт Breaker.

Тогда уравнение точки безубыточности примет вид

10000S + 7500R + 15000B = 5000S + 3600B + 8000B - 18000000

или

5000S+ 3900R + 7000B= 18000000.

Заметим, что существует бесконечное число множеств значений S, R и 5, удовлетво­ряющих данному ограничению: в многопродуктовой модели существует множество точек безубыточности, в то время как для однопродуктовой модели точка безубыточности одна. Поэтому при выпуске нескольких продуктов руководство должно указать дополнитель­ные ограничения, которые позволят найти конкретную точку безубыточности, представ­ляющую интерес. Постоянные затраты придется нести в полном объеме независимо от количества произведенных яхт, поэтому, чтобы добиться минимизации инвестиций, не­обходимо минимизировать суммарные переменные затраты. Таким образом, целевая функция (суммарные переменные затраты) имеет вид

5000S+3600R+8000B.

Полная модель с учетом ограничения безубыточности, предварительно установлен­ных требований и ограничений спроса выглядит следующим образом:

минимизировать 5000S + 3600R + 8000B

при ограничениях

5000S + 3900R + 7000B = 18 000 000,

S>=700,

В>=400,

R<=300,

S>=0, R>=0, B>=0.

Табличная модель, оптимальное решение и параметры для средства Поиск решения представлены на рис. 29.

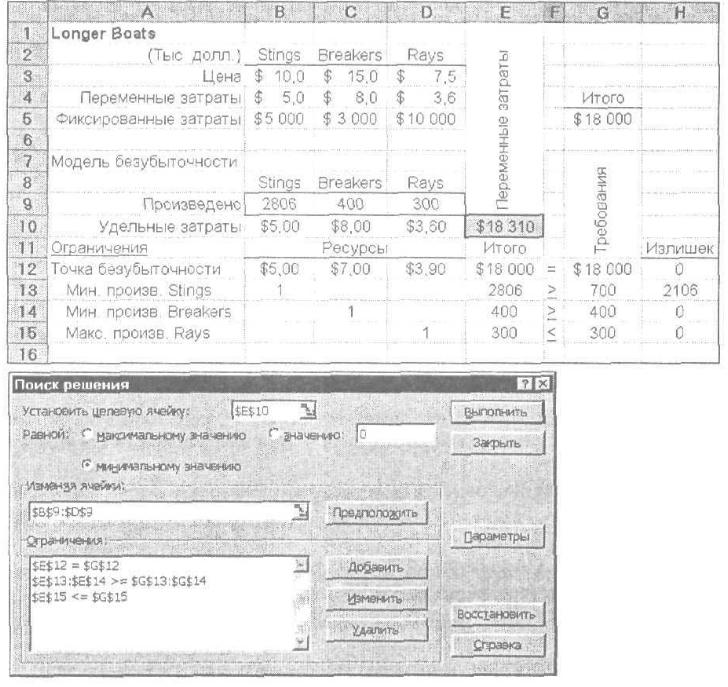Рис. 29. Модель нахождения точки безубыточности

17. Разработка моделей ЛП

Изучая рассмотренные примеры моделей линейного программирования, вы могли убедиться, что их создание сводится к разумной и тщательной спецификации состав­ляющих модели (переменных решения, ограничений, целевой функции и т.д.) в соответ­ствии с символической линейной оптимизационной моделью. Однако в формировании моделей ЛП есть свои ловушки, которых следует избегать. Рассмотрим некоторые ошиб­ки, часто встречающиеся при создании моделей.

• Как всегда при моделировании, не следует сразу излишне детализировать модель, поскольку тогда трудно сформулировать целостную и согласованную модель. При создании табличной версии модели в Excel эти несогласованности превратятся в трудно обнаружимые логические дефекты таблицы. Поэтому лучше начать с формирования минимально достаточного множества переменных решения и ог­раничений. Впоследствии можно усложнить изначально простую модель, добавив дополнительные переменные и ограничения.

• Не следует (по крайней мере на начальных этапах) включать в модель нелинейные зависимости. Старайтесь использовать линейные уравнения, для чего можно в уз­ком диапазоне значений переменных (заданном с помощью дополнительных ог­раничений) аппроксимировать более сложные нелинейные связи линейными за­висимостями. Отметим, что оптимизировать нелинейную модель гораздо труднее). Кроме того, нелинейная оптимизация имеет свои сложности и ловушки. Если же в модель необходимо включить некие нелинейные связи, лучше сначала разработать упрощенную линейную модель, а нелинейные связи добавить позже.

Заметим, что некоторые нелинейные связи можно достаточно просто преобразо­вать в линейные, не утратив общности модели. Предположим, Джим хочет ввести в модель Oak Product ограничение на ассортимент выпуска, которое требует, что­бы при выпуске 3 стульев Captain выпускался по меньшей мере один стул Mate. Можно записать данное ограничение в виде С/М< 3 Это выражение алгебраиче­ски корректно, но функция ограничения является нелинейной по переменной М, поскольку та выступает в качестве знаменателя отношения. С помощью неслож­ного преобразования можно получить эквивалентное неравенство С— ЗМ<= 0, ко­торое уже является линейным по обеим переменным.

• Не следует на ранних этапах заниматься выяснением, какими будут реальные последствия нецелочисленных значений переменных оптимального решения. Однако, как и нелинейные зависимости, требование целочисленности значе­ний переменных вносит дополнительные сложности в процесс оптимизации, поэто­му на первых этапах моделирования это требование лучше не вводить.

• Во многих интересных моделях ЛП принятия решений рассматривается несколько временных периодов (например, задача определения производственного плана на несколько недель при условии, что недели нельзя считать независимыми). В таких случаях лучше сначала моделировать ситуацию для отдельного временного перио­да (например, для одной недели), а затем модифицировать модель, добавляя более сложные формулировки

• В противоположность сказанному выше отметим, что модели ЛП также не должны быль слишком простыми и ограниченными. Например, если модель минимизации затрат не содержит ни одного ограничения, вполне можно получить решение (в реальной жизни не имеющее смысла), что все переменные решения равны нулю, т.е. предлагается минимизировать затраты за счет ликвидации бизнеса. Аналогично в модели максимизации прибыли, не содержащей ни одного ограничения, можно получить "приятное", но нереальное решение с бесконечной прибылью за счет того, что одна или несколько переменных решения в процессе оптимизации модели будут стремиться к бесконечности. В линейном программировании последний результат называется неограниченным решением.

• Нужно очень внимательно относиться к ограничениям в виде равенств и сводить их в моделях ЛП к минимуму, стараясь ограничиться только теми ситуациями, при ко­торых с помощью равенств задаются связи, которые должны сохраниться в модели. Например, в модель можно включить ограничение, отражающее уравнение "Прибыль = доход — затраты", или ограничение, отражающее уравнение материаль­ного баланса "Запасы на конец периода = запасы на начало периода + производство — отгрузка". Однако даже такие ограничения снижают результативность модели. Там, где возможно, такие ограничения лучше задавать в форме неравенств "Прибыль <= ..." или "Запасы на конец периода <=...". В общем случае надо стараться записывать ограничения в виде неравенств, даже если есть основания предполагать, что в оптимальном случае они должны быть равенствами. Позднее, после того как модель будет оптимизирована, можно проверить, действительно ли эти ограничения являются лимитирующими, т.е. выполняется ли равенство, как ожидалось. Если это не так, следует внимательно разобраться, почему этого не происходит.

Включение в модель ограничения в виде равенства увеличивает риск получить че­ресчур ограниченную модель, в результате оптимизации которой получатся реше­ния с низким выигрышем, а в худшем случае допустимых решений может не ока­заться вовсе. Следует особенно внимательно подходить к включению в модель вы­раженных в форме равенств ограничений, отражающих организационную политику. Например, в некой компании XYZ существует неписаное правило: "Назначать одного менеджера (S) на каждые 10 сотрудников (W)", которое пред­полагает, что нужно наложить ограничение W= 10S. Если не существует причины. делающей включение данного ограничения неизбежным, можно улучшить значе­ние целевой функции, не вводя его в модель. Если же такое ограничение включить в модель необходимо, нужно попытаться ввести его в форме неравенства. Напри­мер, приведенное выше ограничение можно сформулировать так: "Одному менеджеру может быть подчинено не более 10 сотрудников", в результате получится ог­раничение W<= =10S. При такой формулировке ограничения в ходе оптимизации модели снижается вероятность получения ответа "допустимых решений не суще­ствует". Более того, может оказаться, что наилучшая стратегия состоит в том, что­бы отказаться от исторически сложившейся традиции назначать менеджера в точной пропорции один к десяти.

• Не следует добавлять ограничения, которые не диктуются моделируемой ситуацией, как это случается, когда в модель с самого начала вводят ограничения, основанные на интуитивных предположениях (зачастую ошибочных) о природе оптимального решения. В таком случае создается самореализующееся предсказание, поскольку решение задачи определено до проведения оптимизации! В результате невозможно узнать, правильны ли были интуитивные соображения. Если же они были ошибоч­ны, результатом оптимизации модели может быть ответ: "Допустимых решений не существует". Например, менеджер считает: "Очевидно, что в данной ситуации нельзя говорить об эффективности, если запас на конец периода будет больше нуля. По­этому для верности я добавлю в модель ограничение Запас на конец периода = О . Та­кие рассуждения не только повышают риск получить чересчур ограниченную мо­дель. Если оптимальное решение задачи без данного ограничения приводит к поло­жительному остатку, менеджер не сможет узнать об этом.

18. Заключение

Ограничения — это математические условия, которые исключают определенные комбинации значений переменных реше­ния. Допустимые решения — это значения переменных, удовлетворяющие всем ограни­чениям. Линейное программирование занимается поиском допустимого решения, опти­мизирующего линейную целевую функцию. Задача линейного программирования — это математическая модель, обладающая следующими свойствами.

1. Линейность целевой функции, которую необходимо максимизировать или мини­мизировать.

1. Линейность ограничений, каждое из которых представляет собой неравенство или равенство.

Учитывая гибкость моделирования на базе электронных таблиц, необходимо следо­вать определенным правилам, чтобы построить табличную модель, обладающую такими свойствами: 1) точно соответствует модели ЛП, 2) легко документируется, 3) имеет фор­му, пригодную для оптимизации с помощью средства Поиск решения, 4) не вызывает проблем при интерпретации отчетов средства Поиск решения. Чтобы успешно hchoj ьзо-вать средство Поиск решения, необходимо придерживаться следующих правил.

1. Все формулы, влияющие на целевую функцию или ограничения, должны быть ли­нейными, если в них прямо или косвенно (через формулы других ячеек) входят переменные решения.

1. Линейная модель является частным случаем нелинейной модели. Однако для средства Поиск решения такое суждение неправомерно: эта надстройка использу­ет разные алгоритмы для оптимизации разных классов моделей. Если в диалого­вом окне Параметры поиска решения не установить опцию Линейная модель и оптимизировать модель ЛП с помощью средства Поиск решения, можно не по­лучить оптимального решения; даже если оптимальное решение будет получено, отчеты для линейной и нелинейной моделей выглядят по-разному.

1. В диалоговом окне Поиск решения при задании правых частей ограничений необ­ходимо ссылаться на ячейки рабочего листа, которые являются константами или которые не будут меняться в процессе оптимизации. Кроме того, не разрешается вводить формулы при определении левых частей ограничений в диалоговом окне Добавление ограничения. Чтобы избежать ошибок и ненужных сложностей, не следует вводить формулы или константы непосредственно в поля левых или пра­вых частей ограничений диалогового окна Добавление ограничения. Рекоменду­ется помешать формулы и константы в ячейки таблицы, а в полях диалогового ок­на Добавление ограничения указывать адреса соответствующих ячеек.

1. В моделях большого размера полезно присваивать имена диапазонам ячеек пере­менных решения, ячейке показателя эффективности, группам ячеек, содержащих левые части ограничений одного знака, и группам ячеек, содержащих правые час­ти ограничений одного знака.

Перед выполнением процесса оптимизации в диалоговом окне Поиск решения нужно указать целевую ячейку, изменяемые ячейки, ограничения и установить флажок Линей­ная модель. Кроме того, если отрицательные значения переменных решения не имеют смысла, нужно установить флажок опции Неотрицательные значения. После заверше­ния оптимизации на экране появится диалоговое окно Результаты поиска решения, со­держащее сообщения о завершении вычислений и позволяющее создать один или не­сколько отчетов о поиске решения.

Мы привели несколько примеров, демонстрирующих переход от реальной ситуации к символической модели ЛП. Если целью является увеличение прибыли, создается мо­дель максимизации, а если цель— уменьшить затраты, получится модель минимизации. Ограничения записываются в виде неравенств со знаком <= или >=. В некоторых случаях необходимо ввести ограничения в виде равенств.

Основные термины

Допустимое решение. Решение, удовлетворяющее всем ограничениям модели, включая условия неотрицательности.

Значения решения. Набор числовых значений переменных решения.

Излишек. Показывает, на сколько вычисленная при оптимальных значениях переменных левая часть ограничения вида "2" превышает правую часть. Излишек всегда неотрицателен.

Лимитирующее ограничение. Ограничение, в котором при оптимальных значениях переменных ле­вая часть равна правой.

Линейная функция. Функция, в которую все переменные входят в виде отдельных членов. В такой функции нет степеней, отличных от 1, логарифмических, экспоненциальных, тригонометри­ческих или подобных выражений.

Модель условной оптимизации. Модель, цель которой состоит в том, чтобы найти значения пере­менных решения, оптимизирующие целевую функцию при условии соблюдения ограничений.

Невозвратные издержки. Затраты, значения которых уже определены, и поэтому на них не могут повлиять будущие решения.

Ограничение в форме неравенства. Ограничение, требующее, чтобы некая функция переменных решения была больше или равна (>=) или меньше или равна (<=) определенной константы.

Ограничение в форме равенства. Ограничение, требующее, чтобы некая функция переменных ре­шения была в точности равна некоторой константе.

Ограничение. Математическое выражение в форме неравенства или равенства, которому должны удовлетворять переменные модели.

Оптимальное решение. Допустимое решение, оптимизирующее целевую функцию (т.е. обеспечи­вающее максимум или минимум целевой функции).

Оптимальный ассортимент продукции. Тоже, что и оптимальный производственный план.

Оптимальный производственный план. Оптимальное решение производственной модели, опреде­ляющее оптимальные количества производимых продуктов.

Оптимизировать. Максимизировать или минимизировать целевую функцию.

Переменные затраты. Затраты, значения которых будут определяться выбранным решением.

Переменные решения. Переменные, значениями которых управляет человек, принимающий решение.

Поиск решения. Надстройка (средство) Excel, которая может оптимизировать табличные модели Л П.

Правая часть ограничения. Число, стоящее в правой части неравенства, задающего ограничение.

Резерв. Показывает, на сколько левая часть ограничения вида "<=.", вычисленная при оптимальных значениях переменных, меньше, чем правая часть. Резерв всегда принимает неотрицательные значения.

Символическая модель Л П. Математическое представление задачи линейного программирования.

Условие целочисленности. Требование, чтобы одна или несколько переменных модели принимали только целочисленные значения.

Условия неотрицательности. Условия модели, требующие, чтобы переменные решения принимали только неотрицательные (положительные или нулевые) значения.

Функция ограничения. Левая часть неравенства, задающего ограничение; зависит от переменных решения.

Целевая функция. В каждой задаче линейного программирования имеется линейная целевая функция, представляющая показатель эффективности, которую необходимо максимизировать или минимизировать.

Целочисленное программирование. Модель, в которой одна или несколько переменных могут при­нимать только целые значения.

Контрольные вопросы для самопроверки (ответы приведены ниже)

Да / нет

1. В моделировании условия, сужающие область допустимых решений, называются ограничениями.

1. Модель ЛП не обязательно содержит ограничения.

1. Любая модель, содержащая целевую функцию, ограничения и переменные реше­ния, является моделью линейного программирования.

1. Ограничения задаются неравенствами типа ">=".

1. Условия неотрицательности означают, что все переменные решения должны быть положительными.

1. Поскольку дробные значения переменных решения могут не иметь физического смысла, на практике оптимальное решение задачи ЛП часто округляется до цело­численных значений.

1. Все ограничения в линейных моделях являются неравенствами.

1. Правильное определение переменных решения является ключевым этапом сфор­мирования модели.

1. Целевая функция модели минимизации затрат должна учитывать только перемен­ные затраты.

10. Менеджер должен знать, каким образом реальная ситуация формализована в мо­дели ЛП, поскольку рано или поздно ему придется оценить правильность данной модели.