Variance

Вычисляет дисперсию вдоль указанного размера входа или за время.

Display

Отображает численное значение результатов вычислений.

To Workspace Создает массив или структуру данных в рабочей области Matlab.

Sign

Преобразует входной сигнал в бинарный сигнал.

Полученные результаты моделирования при данных значениях математического ожидания и дисперсии

Мат. ожидание: 0,1 Дисперсия: 0,1

Мат. ожидание:0,1; Дисперсия: 1

Мат. ожидание: 0,1 Дисперсия: 0,5

Мат. ожидание:1 Дисперсия: 0,1

Мат. ожидание: 1Дисперсия: 1

Мат. ожидание: 1Дисперсия: 0,5

Мат. ожидание: -0,3Дисперсия: 1

Мат. ожидание: -0,3 Дисперсия: 0,5

Мат. ожидание: -0,3

Дисперсия:0, 1

Вывод:

В ходе лабораторной работы я исследовал закона распределения бимодальной помехи от математического ожидания и дисперсии.

Исходя из полученных гистограмм мы можем утверждать, что математическое ожидание влияет на распределение сигнала намного сильнее, чем дисперсия. При изменении математического ожидания хорошо видно изменения распределения между левым и правым пиками. При увеличении математического ожидания левый пик уменьшается, а правый увеличивается. Дисперсия не оказывает влияние.

Тема: Зависимость формы определения полосовой помехи от дисперсии и мат. Ожидания

Цель работы: Зависимость формы определения полосовой помехи от дисперсии и мат. ожидания

Теоретические сведения

Полосовая помеха – помеха находящаяся в определенной полосе частот

Ход работы

Лабораторная схема №1 чтобы рассмотреть спектр помехи и фильтра

Спектр фильтра и помехи выглядят следующим образом:

Лабораторная схема для изучения закона распределения полосовой помехи в зависимости от мат. ожидания и дисперсии:

Описание блоков

Gaussian Noise Generator

Генерирует гауссовский шум со значением математического ожидания и дисперсии.

Histogram

Генерирует гистограмму элементов в указанной размерности ввода или через время (бегущая гистограмма)

Maximum

Вычисляет максимальное значение вдоль указанной размерности входа или за времени

Minimum

Вычисляет минимальное значение вдоль указанной размерности входа или за время

Mean

Вычисляет среднее значение по указанной размерности входа или за время.

Variance

Вычисляет дисперсию вдоль указанного размера входа или за время.

Display

Отображает численное значение результатов вычислений.

To Workspace Создает массив или структуру данных в рабочей области Matlab.

Mux - мультиплексор Digital filter design – цифровой фильтр со следующими параметрами:

Мат. ожидание: 0,1 Дисперсия: 0,1

Мат. ожидание:0,1; Дисперсия: 1

Мат. ожидание: 0,1 Дисперсия: 0,5

Мат. ожидание:1 Дисперсия: 0,1

Мат. ожидание: 1Дисперсия: 1

Мат. ожидание: 1Дисперсия: 0,5

Мат. ожидание: -0,3Дисперсия: 0.5

Мат. ожидание: -0,3 Дисперсия: 1

Мат. ожидание: -0,3

Дисперсия:0, 1

Вывод: В ходе лабораторной работы я исследовал закон распределения полосовой помехи от математического ожидания и дисперсии.

Исходя из полученных гистограмм мы можем утверждать что математическое ожидание влияет на положение центрального пика, при увеличении мат. ожидания центральное значение перемещается по оси Ох вверх, а при уменьшении значения перемещается по оси Ох вниз.

Дисперсия влияет на величину разброса значений. С увеличением дисперсии увеличивается разброс значений. Амплитуда зависит от величины дисперсии сигнала. Амплитуда уменьшается с увеличением дисперсии.

Тема: Исследование помехоустойчивости схемы с АМ, ЧМ, ФМ.

Цель работы: Исследовать зависимость количества ошибок от соотношения сигнал/шум при передаче информации через канал с аддитивной помехой при различных видах модуляции.

Теоретические сведения:

Амплитудная модуляция - вид модуляции колебаний, при котором передаваемый сигнал управляет амплитудой несущего ВЧ колебания.

ЧАСТОТНАЯ МОДУЛЯЦИЯ - вид модуляции колебаний, при котором передаваемый сигнал управляет частотой несущего ВЧ колебания.

ФАЗОВАЯ МОДУЛЯЦИЯ - вид модуляции колебаний, при котором передаваемый сигнал управляет фазой несущего ВЧ колебания.

АДДИТИВНАЯ ПОМЕХА представляет собой случайный сигнал, который накладывается на полезные сигналы, передаваемые по каналам (трактам) передачи.

Общая схема лабораторной модели в среде Matlab

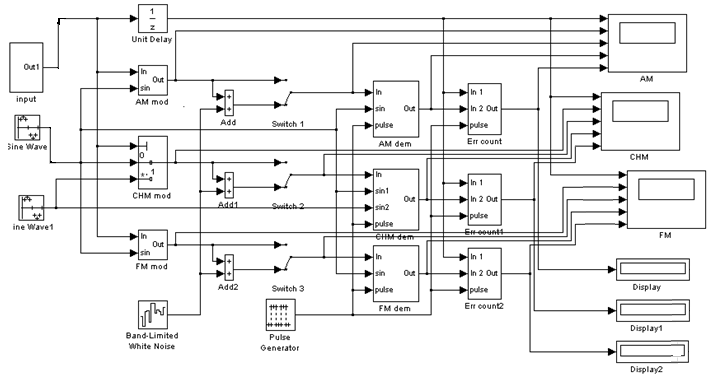
Описание блоков

INPUT

Генерирует входной сигнал.

AM mod

Амплитуда несущего колебания изменяется по закону входного сигнала.

Предусмотрена возможность переключения между режимами «без возврата к нулю» (NRZ) и «с возвратом к нулю» (RZ).

CHM mod

Частота несущего колебания изменяется по закону входного сигнала.

FM mod

Фаза несущего колебания изменяется по закону входного сигнала.

AM dem

Возвращает сигнал к исходной форме.

CHM dem

Возвращает сигнал к исходной форме.

FM dem

Возвращает сигнал к исходной форме.

Err count, Err count1, Err count2

Производит подсчет количества ошибок.

ADD, ADD1, ADD2

Модель канала с аддитивной помехой.

Switch 1, Switch 2, Switch 3

Добавляет помеху в канал.

Band-limited white noise

Генерирует помеху с заданными параметрами.

Display, Display1, Display2

Отображает количество ошибок .

AM, CHM, FM

Отображает сигнал на разных стадиях обработки.

Полученные результаты моделирования при данных значениях частоты и амплитуды помехи:

АМ

Noise power	Sample time	Количество ошибок
100	0.01	0
100	0.001	0
100	0.0001	46
10	0.0001	41
1	0.0001	39

ЧМ

Noise power	Sample time	Количество ошибок
100	0.01	28
100	0.001	33
100	0.0001	50
10	0.0001	43
1	0.0001	41

ФМ

Noise power	Sample time	Количество ошибок
100	0.01	0
100	0.001	0
100	0.0001	32
10	0.0001	14
1	0.0001	0

Вывод:

В ходе лабораторной работы была исследована зависимость количества ошибок от частоты и уровня аддитивной помехи. Выявлены следующие закономерности:

Амплитудная модуляция невосприимчива к низкочастотной помехе, при этом на высокой частоте зависимость от амплитуды помехи незначительна.

Частотная модуляция сильно зависит от амплитуды и частоты помехи на всем диапазоне значений.

Фазовая модуляция невосприимчива к низкочастотной помехе, при этом на высокой частоте проявляется зависимость от амплитуды помехи.

Наиболее помехоустойчивой для передачи бинарного сигнала по результатам проведенного моделирования является фазовая модуляция.

Тема: Блок нелинейного преобразования

Цель работы: Из сигнала с двумя пиками сделать сигнал с одним пиком

Теоретически сведения

Нелинейное преобразование – преобразование в ходе которого изменяется спектральная составляющая сигнала.

Ход работы

Общая схема лабораторной модели в среде Matlab

Описание блоков

Gaussian Noise Generator

Генерирует гауссовский шум со значением математического ожидания и дисперсии.

Histogram

Генерирует гистограмму элементов в указанной размерности ввода или через время (бегущая гистограмма)

Maximum

Вычисляет максимальное значение вдоль указанной размерности входа или за времени

Minimum

Вычисляет минимальное значение вдоль указанной размерности входа или за время

Mean

Вычисляет среднее значение по указанной размерности входа или за время.